математика

3.Вычисление площадей плоских фигур в декартовой системе координат

Исходя из геометрического смысла определенного интеграла площадь криволинейной трапеции, расположенной выше оси абсцисс ( f ( x ) ≥ 0 ), равна соответствующему оп-

ределенному интегралу:

b

S = ∫ f ( x )dx .

a

В общем случае, площадь фигуры, ограниченной кривыми y = f1( x ) и y = f2 ( x ) , прямыми x = a и x = b , при

	b
условии, что	f2 ( x ) ≥ f1( x ) , равна S = ∫(f2 ( x ) − f1( x ))dx .
	a
Пример
Найти	площадь фигуры, ограниченной линиями
y = −x2 , y = x − 2 .

Решение

Изобразим кривые на чертеже. Решив систему

		y = −x2
		y = x − 2 ,					получаем координаты двух точек пересе-
	чения (1; -1) и (-2; -4). Искомая площадь S криволинейно-
	го треугольника						можно представить как разность площадей
	(рис.3).
	1						1
	S = ∫( −x2 −( x − 2 ))dx = = ∫(−x2 − x + 2)dx =
		−2							−2
	= (−	x3		−	x2	+ 2x)			1−2 = 9 = 4,5 .
	3			2					2
							31

Рис. 3

4.Вычисление площадей плоских фигур в полярной системе координат

Фигура, ограниченная графиком функции (рис.4) r = r(ϕ ) и двумя лучами ϕ = α и ϕ = β , называется криво-

линейным сектором. Его площадь вычисляется по формуле

S = 1 ∫β r2 (ϕ )dϕ . 2 α

32

r(ϕ)

ϕ=β

ϕ=α

0

ρ

Рис.4

Если плоская фигура имеет более сложную форму, то необходимо разбить ее лучами, выходящими из полюса на криволинейные сектора, к которым применять либо полученную формулу, либо формулу для сектора, ограниченного

двумя непрерывными линиями r = r1 ( ϕ) и r = r2 ( ϕ)

(рис. 5).

ϕ=β r1(ϕ)

r2(ϕ) ϕ=α

0

ρ

Рис.5

33

S = 1 ∫β ( r12 (ϕ ) − r2 2 (ϕ ))dϕ . 2 α

Пример

Найти площадь кривой, ограниченной кривой r = 2 cos 3ϕ (рис. 6).

π

6

		ρ
0

Рис.6

Решение

Так как площади всех лепестков «трехлепестковой розы» равны, а каждый лепесток симметричен относительно своей оси, то найдем площадь половины одного лепестка и умножим ее на 6, получим площадь искомой фигуры:

			π	π
S1	=	1	∫6	( 2 cos 3ϕ )2 dϕ = 2∫6	1 + cos 6ϕ dϕ =
		2	0	0	2

34

ππ

	= (ϕ	6	+	sin 6ϕ 6		) = (	π	+ 0)	=	π	.
		0		6	0		6			6

Тогда площадь всей фигуры равна

S= 6S1 = 6 π6 = π .

5.Вычисление длины дуги плоской кривой

Пусть в прямоугольных координатах дана плоская кривая АВ, уравнение которой y = f ( x ) , где a ≤ x ≤ b .

Если функция			f ( x ) и ее производная непрерывны на
отрезке [a;b], то кривая АВ имеет длину, равную
b
l = ∫		′		2	dx .
	1 +( f ( x ))
a
Если линия задана уравнением x = ϕ( y ),						c ≤ y ≤ d , то
ее длина вычисляется по формуле
d
l = ∫		′		2	dy .
	1 +( ϕ( y ))
c
Если уравнение кривой АВ задано в параметрической
x = x( t )		, α ≤ t ≤ β , причем x( t ), y( t )				– непрерыв-
форме	= y( t )
y

ные функции с непрерывными производными и a = x(α ) , b = x( β) , то длина кривой АВ находится по формуле

β
l = ∫	′	2	′	2	dt .
	( x ( t ))		+( y ( t ))

α

35

Примеры

1) Найти длину дуги кривой y = ln( 2x ) на промежутке

3 ≤ x ≤ 8 .

Решение

y′ =

2

=

1

+

( y′)

2

=1 +

1

=

1

+ x2

x

, 1

и

2x

x2

x2

tdt

l = ∫

1

+ x2 dx

= t =

1 + x

2

; x

=

t

2

−1; dx =

t2 −1 =

8

3

x

x = 3 t = 2; x = 8 t = 3

3

t

2

dt

3

1

3 +

1 ln

t −1

3 = 1 +

1 ln 3 .

= ∫

=

∫( 1

+

)dt = t

2

2

2

t

−1

2

t

−1

2

2

t +1

2

2 2

2)

Найти длину дуги кривой x = 2 cos3 t, y = 2 sin3 t

при 0 ≤ t ≤ π4 .

Решение

Найдем значение производных:

x′ = −6 cos2 t sin t , y′ = 6 sin2 t cos t .

π

Отсюда l = ∫4 36 cos4 t sin2 t + 36 sin4 t cos2 tdt =

0

36

π	π	π

= ∫4	6 cos t sin tdt = 3∫4	sin 2tdt = − 3 cos 2t 4 =		3 = 1,5 .
0	0	2	0	2
	6. Вычисление объема тела вращения
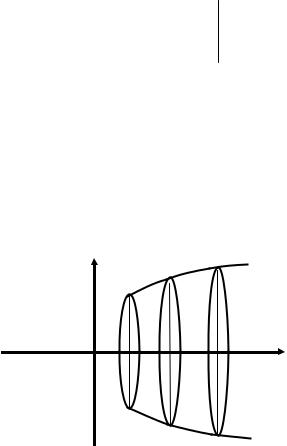
	Объем тела ( рис.7), образованного			вращением во-
круг оси Оx криволинейной трапеции,				ограниченной не-
прерывной кривой		y = f (x) , осью Оx	и прямыми x = a и

b

x = b , вычисляется по формуле Vox = π∫ f 2 ( x )dx .

	a
y	y=f(x)

a

b

х

Рис. 7

Если криволинейная трапеция ограничена графиком непрерывной функции x = ϕ( y ) и прямыми x = 0, y = c и

y = d( c < d ) , то объем тела, полученного вращением этой трапеции вокруг оси Oy, будет равен

d

Voy = π∫x2 ( y )dy .

c

37

Пример

Найти объем тела, полученного от вращения вокруг оси ординат плоской фигуры, ограниченной линиями y = x2 , y = x3 .

Решение

Сделаем рисунок (рис. 8) и убедимся, что искомый объем получится в результате разности двух объемов: объема V1 , полученного от вращения вокруг оси Oy фигуры,

ограниченной линиями x = 3 y , x = 0, y =1, и объема тела

вращения V2 x = 0, y =1 .

Тогда

1

V1 = π∫( 3

0

1

V2 = π∫(

0

фигуры, ограниченной линиями x = y ,

			5
y )	2	dy = π	3 y	3		1	=		3π		;
			5			0				5
y )	2	dy = π	y2		1	=		π		.
			2		0			2

Окончательно V =V1 −V2 = 35π − π2 = 10π = 0,1π.

38

y=x3 y=x2

Рис. 8

Задания для контрольной работы № 5

201-210. Вычислите несобственный интеграл или установите его расходимость.

∞

dx

∞

201.

∫

.

202. ∫ln xdx .

x(x −1)

2

1

x

4

dx

∞

dx

203. ∫3

204. ∫e

.

.

( x −3 )2

x ln2 x

∞

dx

2

xdx

205.

∫0

206. ∫0

.

.

x2 + 4x +8

( x2 − 4 )3

1

x

2

dx 3 .

∞

207.

∫

208. ∫xe−x dx .

0

1 − x

0

39

0	dx			∞	6x3	2	+2	5 dx .
209. ∫			.	210. ∫
	( x + 4 )	4
−4				1		x

211-220. Найдите площадь фигуры, ограниченной линиями. Сделайте чертеж.

211. a) y =		x2	, y =	4 − 2 x2			;	216.	а) y = x2 −3x, y = 4 −3x;
	3			3					б) ρ = 2sin 2ϕ
б)	ρ = 2 +cosϕ .
212. а) x + y = 2, x = 2, y = 2;								217.	а) y = 3 − x2 , y =1 − x ;
б) ρ =1 +cos 2ϕ .									б) ρ = 2cos 2ϕ .
213.	а) 2 y = x2 , y =				3	− x ;			а) y = 3x2 +1, y = 3x + 7 ;
								218.	б) ρ = 3cos3ϕ.
				2

б) ρ = 2 −cosϕ .

214.а) y = 4 – x2, y = x2 –2x;	219.	а) y = 2x − x2 , y
б) ρ =1 −sin 2ϕ .
		б) ρ =1 −sinϕ .
215.а) y = (x – 1)2, y2 = x – 1;	220.	а) y = x2 − 2x, y
б) ρ = 2 +sinϕ .		б) ρ = 2 − sinϕ .

=−x ;

=x ;

221-230. Найти длину дуги с помощью определенного интеграла.

221.Кривой x = 2 cos3 t, y = 2 sin3 t , ( 0 ≤ t ≤ π4 ).

222.Кривойx = 5( t − sin t ) , y = 5(1 −cos t), ( 0 ≤ t ≤ π ).

223.Кривой y = ln(sin x ) , ( π4 ≤ t ≤ π2 ).

224.Кривойx = 4(cos t + t sin t ) , y = 4(sin t −t cos t ) , ( 0 ≤ t ≤ 2π ).

40