Линейная_алгебра_УП_очная_ЭлРес

		4 x1 + x2 –5x3 ≥ 4,				работы
		2x1 + 3x2 + x3 ≥ 2,			α0 = (0, 0, 3).
		xj ≥ 0, j=1, 2, 3,
2.2.	f(X) = 2x1 + x2 + 3x3		(max),					МБИ
		x1 + 7 x2 + x3 ≤ 25,
		x1 + 2x2 + 2x3 ≤ 45,
		–4x1 + x2 + x3 ≤ 8,		α0 = (5, 0, 20).
		xj ≥ 0, j=1, 2, 3,
2.3.	f(X) = 60x1 + 21x2 + 4x3 (min),
		20 x1 + 7 x2 – 3x3	≥ 4,
		самостоятельной
		15 x1 + 2x2 +x3 ≥ 1,				ВПО
		2x1 + 2x2 + x3 ≥ 3,			α0 = (0, 1, 1).
		xj ≥ 0, j=1, 2, 3,							.
Задача 3. Найти оптимальное решение данной задачи, решив двойственную к
ней задачу.							2013		г
3.1.	f(X) = 6x1 + 9x2 +15x3		(min),
		– x1 + x2 + 3x3 ≥ 4,			ЧОУ
		2 x1 + x2 – x3 ≥ 2,
		xj ≥ 0, j=1, 2, 3.
3.2..	f(X) = 6x1 + 2x2 + 5x3		(min),
		–3 x1 + x2 + x3 ≥ 2,			Москва
		2 x1 – 4x2 – x3 ≥ 3,
		xj ≥ 0, j=1, 2, 3,
		студентов
3.3	f(X) = 6x1 + 2x2 + 5x3 (min),
		–3 x1 + x2 + x3 ≥ 1,
		2 x1 – 4x2 – x3 ≥ 2,
		xj ≥ 0, j=1, 2, 3,
3.4.	f(X) = 2x1 + x2 +5x3 (min),
		x1 – 2 x2 + x3 ≥ 3,
		2x1 – 5x2 + 3x3 ≥ 5,
Для		3x1 + x2 + 4x3 ≥ 7,
		xj ≥ 0, j=1, 2, 3,
	f(X) = x1 + 11x2 +3x3 (min),
3.5.

3 x1 – 2 x2 + 2x3 ≥ 2, x1 + x2 +2x3 ≥ 3, –2x1 + 3x2 – 3x3 ≥ –5,

xj ≥ 0, j=1, 2, 3,

101

Задача 4. Является ли данный вектор α оптимальным решением задачи ЛП?

4.1.f(X) = 7x1 + 2x2 + 2x3 + 5x4 (max),

3 x1 – x2 + x3 + 2x4 = 7,
x1 + 2x2 –x3 + x4 = 2,		МБИ
4x2 + 3x3 + 11x4 = 11,
xj ≥ 0, j=1, 2, 3, 4,	α = (0, 0, 1, 3).

4.2.	f(X) = 4x1 – 5x2 + x3 – 3x4 (min),						работы
	x1 + x2 + x3 + x4 = 17,
	2x1 – x2 +–x3 – 2x4 = 7,
	xj ≥ 0, j=1, 2, 3, 4,					α = (0, 5, 18, 0).
4.3.	f(X) = x1 + 4x2 + 3x3 + x4 (min),
	самостоятельной						ВПО
	8 x1	+ 7 x2 + 6 x3 + 28x4			= 28,
	3x2	–x3 +5x4 = 5,							.
	xj ≥ 0, j=1, 2, 3, 4,					α = (1, 2, 1, 0).		2013	г
4.4.	f(X) = x1 + 5x2 –x3 (max),
	4x1 + x2 + x3 ≤ 12,
	x1 + 3x2 + x3 ≥ 3,					ЧОУ
	2x1 + x2 – 4x3 ≤ 2,
	xj ≥ 0, j=1, 2, 3,			α = (0, 2, 0) .
4.5.	f(X) = 3x1 + 2x2 – x3 (min),
	x1 – x2 – 2x3 ≥ –5,					Москва
	x1 + 3x2 –2x3 ≥ 4,
Для	–x1	+ x2 + x3 ≥ 5,
	студентов
	xj ≥ 0, j=1, 2, 3,			α = (0, 5, 0)
4.6.	f(X) = 5x1 – 3x2 +16x3		(min),

x1 + 2 x2 + 3x3 = 4, x1 – 2x2 +8x3 ≥ 5, x1 ≥ 0, x2 ≥ 0.

102

2.11. Экономическое содержание симплекс алгоритма и двойственности

Экономическую трактовку переходов от одной симплекс таблицы к другой, элементов симплексных таблиц и двойственн сти проведем на примере рационального использования предприятием техн л гических способов и ресурсов при производстве некоторой продукции.

Пример. Предприятие может производить продукцию, используя четыре технологических способа и три вида ресурсов. Технологическая матрица А – затрат ресурсов при производстве единицы п одукции за единицу времени

использования технологического способа, вектор В - наличия ресурсов и вектор
С – количества	единиц				продукции,			работы		единицу времени
								произведенной за
использования технологических сп с б в, заданы в виде:									МБИ
										.
4		3	4	5		208
	2	5	0	2				C (36,14,25,50).
А					,	B 107	,
	3	1	2	5
						181
Требуется составить						производственную программу,				г
										обеспечивающую

предприятию наибольший выпуск продукции при использовании имеющихся

технологических способов и наличных ресурсов.

ВПО

Математическая пос ановка. Найти вектор Х=(x1, x2, x3, x4),

доставляющий наибольшее значение целевой функции

2013

φ(X) = 36x1+ 14x2 + 25x3

+ 50x4

,

(1)

на множестве допустимых решений, заданном огр ничениями

4x1

+3x2

+4x3

+5x4

≤208,

2x1

+5x2

ЧОУ

≤107,

(2)

+2x3

+2x4

x1

+x2

+5x4

≤181,

Москва

Для

самостоятельной

студентов

(3)

x1 0, x2

0, x3 0, x4 0.

Нахождение оптималь ого решения поставленной задачи будем

осуществлять

последователь ого

улучшения

плана

для нахождения

наименьшего значения функции

f(X)= - φ(X) = -36x1- 14x2 - 25x3 - 50x4

(1.1)

на множестве допустимых решений, заданном ограничениями (2) и (3).

Приведем ограничения (2) к системе равенств

4x1 +3x2 +4x3

+5x4

+x5

=208,

(2.1)

2x1

+5x2

+2x4

+x6

=107,

3x1

+x2

+2x3

+5x4

x7

=181

103

работы
при помощи дополнительных неотрицательных переменных х5, х6, х7	, которые,

по смыслу, являются остатками ресурсов после выполнения соответствующей производственной программы.

Среди всех решений системы уравнений (2.1), удовле воряющих условию

х1 0, х2 0, … , х5 0, … , х7 0,	МБИ	(3.1)

найдем решение, при котором функция (1.1) примет наименьшее значение. Так как правые части всех уравнений системы (2.1) неотрицательны и

каждое уравнение содержит разрешенную переменную, то приравняв к нулю свободные переменные х1, х2, х3, х4, получаем опо ное решение

x1=0, x2=0, x3=0, x4=0, x5=208, x6=107, x7=181,			(4.1)
самостоятельной	ВПО
в котором первые четыре компоненты
x1=0, x2=0, x3=0, x4=0			(4.1.1)
соответствуют программе, по к т р й предприятие ничего не производит.
			.
За единицу времени использова ия 4-го технологического способа
			г
производится продукции [смотри (1)] больше, чем при использовании любого
		2013
другого технологического способа. Поэтому целесообразно в первую очередь

включить в план производства испо ьзование 4-го технологического способа.
							ЧОУ
Для этого систему уравнений (2.1) перепишем в виде
		x5		=208	-4x1	-3x2	-4x3	-5x4	(2.2)
		x6		=107	-2x1	-5x2		-2x4
		x7 =181 -3x1				-x2	-2x3	-5x4
возможное время,				т.е., при х4		= 181/5.		МоскваПодставив его в (2.2), получаем для
			студентовх1=0,х2=0,х3=0,х4= 181 .						(4.2.1)
	При х1=х2=х3=0 и не отрицательности базисных переменных х5 0, х6 0,
х7 0 получаем		и тему неравенств
208	-5x4	≥0				x4	≤208/5		0 х4 181/5.
107	-2x4	≥0				x4	≤107/5
181	-5x4	≥0				x4	≤181/5

Т ким обр зом, р сурсы предприятия позволяют увеличить производство продукции при использовании 4-го технологического способа максимально

Для
системы уравнений (2.1) новое опорное решение
х1=0, х2=0, х3=0, х4=	181	, x5=27, x6=	173	, x7=0,	(4.2)
	5		5

Это опорное решение определяет новую производственную программу

5

104

Замечание. ►Чтобы получить опорное решение (4.2) достаточно было в системе (2.1) неизвестную х4 сделать разрешенной. Прав е части уравнений остануться неотрицательными, если разрешающий элемент а34= 5 выбирается согласно критерию

решение, совпадающее с (4.2), в котором первые 4-е компоненты определяют

							b							,						(5)
						min				i
							ai 4
							ai 4 0
т.е., min { 208 ,107 ,														181 }=181 .
						5			2					5	5
После преобразования Жордана с выб анным разрешающим элементом,
получаем общее решение системы уравнений (2.1)
				x1	+ 2x2 + 2x3										+ x5	работы
																	- x7		= 27
		4							4								2			МБИ
				x1	+	23 x2	-					x3			+ x6 -			x7 =		173	.	(2.3)
5									5								5			5
						5
	3		x1		+	1 x2	+			2		x3 + x4				+	1 x7 =			181
5									5											5
						5											5
Приравняв к нулю свободные переменные х1, х2, х3, х7, получаем опорное
самостоятельной																ВПО			2013		г

ЧОУ		5 5	5
производственную программу (4.2.1), т.е.
х1=0, х2=0, х3=0, х4=	181 .	◄
	5
Далее необходимо ответить на вопрос, обеспечивает ли программа (4.2.1)

наибольшее производство продукции при существующих ограничениях.								Для
				Москва
этого выразим из п следнего уравнения системы (2.3) разрешенную
переменную х4 через свободные переменные х1, х2, х3, х7 , т.е. х4 = 181 -						3	x1	- 1
	2			27студентов137 5 181 5 27
x2 -		x3 -	1 x7 , и под тавив в целевую фун цию (1.1), получим
5			5
				f(x) = -1810-6х1-4х2-5х3+10х7.	(1.2)

В целевой функции (1.2) переменные, характеризующие производство продукции по 1-му, 2-му и 3-му технологическим способам, имеют отрицательные коэффици нты. Следовательно, производственную программу

Для	ai1 0
(4.2.1)	можно	улучшить,	если использовать 1-й, или 2-й, или 3-й

технологические способы. Наибольшее уменьшение функции f(x) возможно при использовании 1-го технологического способа, т.е. при увеличении переменной х1. Поэ ому, используя критерий (5), находим

min 1 ; 45 ; 35 1

105

и соответствующий ему разрешающий элемент а11=1. Исключаем переменную х1 из всех уравнений системы (2.3), кроме 1-го уравнения. Получим очередное общее решение системы (2.1) и соответствующее ему опорное решение, для проверки оптимальности которого выразим переменную х1 через новые свободные переменные х2, х3, х5, х7 иподставим в целевую функцию (1.2) и т.д.

Замечание. ►Тот же результат можно получить иначе, а именно, вернутся к началу решения поставленной задачи и представить соотношение (1.1) в виде уравнения

					36х1 + 14х2 + 25х3 + 50х4 = – f(x).																(1.3)
Затем добавить уравнение (1.3) к системе (2.3) и получить систему
уравнений														работы					МБИ
	x1				+	2x2	+ 2x3					+ x5		- x7 = 27,						.
		4		x1	+	23 x2	-	4		x3			+ x6	-	2	x7 =		173	,		(2.3.1)
	5							5							5			5
						5
	3					1		2							1			181
			x1		+	5 x2	+				x3	+ x4		+	5 x7		=		,	г
		5							5									5
	36х1 + 14х2 + 25х3 + 50х4														ВПО		= – f(x).
В последнем					уравнении системы (2.3.1)										положительный наибольший
												ЧОУ						2013
	самостоятельной

коэффициент, равный 4= 50, соответствует переменной х4. Исключим

переменную х4 из последнего уравнения. Для этого, умножив третье уравнение

ДляПервые 3-истудентовуравн ния системы Москва(2.3.2) представляют общее решение системы уравнений (2.1) и определяют опорное решение (4.2),

системы (2.3.1) на (-50) и прибавив к четвертому уравнению, получим систему

	x1			+	2x2	+ 2x3					+ x5	- x7			= 27,
	4		x1	+	23 x2	-	4			x3	+ x6	-	2	x7	=	173	,		(2.3.2)
	5						5						5			5
					5
	3	x1		+	1 x2	+		2		x3 + x4		+	1 x7		=	181		,
	5						5									5
					5								5

6x1 + 4x2 + 5x3 -10x7 = -1810 – f(x).

соответствующее производственной программе (4.2.1).Последнее уравнение системы (2.3.2) соответствует функции цели (1.2), выраженной через свободные переменные х1, х2, х3, х7 . Наличие положительных коэффициентов j при переменных в по леднем уравнении системы (2.3.2), указывает на то, что производственная программа не является оптимальной и необходимо продолжить ее улучшение.

106

3x2 - 12 x3	- 4 x5 + x6	работы+ 2 x7 = 13 ,	(2.3.3)
Для этого в план производства		дополнительно	вводится 1-й

технологический способ, так как с помощью уравнения (1.2), которое соответствует последнему уравнению системы (2.3.2), был установлен

положительный наибольший коэффициент, равный	max { j}= max{6, 4, 5} = 6 =
	j	МБИ
1. Поэтому свободную переменную х1 делаем
	разрешенной, используя

преобразование Жордана с разрешающим элементом а11=1, выбранному согласно критерию (5), и получаем систему

	x1 + 2x2 +	2x3		+ x5		-		x7 = 27,
		5	5				5
	- x2 -	4 x3 + x4 -		3	x5	+	4 x7 = 20,
			5
		5					5

8x2 -7x3

-6x5

-4x7 = -1972 – f(x),

Первые 3-и уравнения

системы

(2.3.3)

являются

общим

решением

системы уравнений (2.1) и соответствуют опорному решению

.

г

x1=27, x2=0, x3=0, x4=20, x5=0, x6=13, x7=0,

(4.3)

которое определяет производственную программуВПО

с использованием 1-го

и 4-го технологических способов

x1=27,

x2=0, x3=0, x4=20.

(4.3.1)

При производстве продукции по этой программе полностью

используются ресурсы 1-го

и

3-го

видов (х5=0, х7=0)

и остаются не

использованными ресурсы 2-го вида (х6=13).

2013

Среди

коэффициен ов

при

неизвестных

левой

части

последнего

уравнения

ЧОУ

системы (2.3.3) нет ни одного положительного. Это соответствует

тому, что целевая функция

f(x) = -1972 + 8х2 + 7х3 + 6х5 + 4х7

(1.3)

не может быть у еньшенной и ее наименьшее значение равно fmin(х) = -1972 при x2=0, x3=0, x5=0, x7=0. Следовательно, возвращаясь к исходной задаче, можно утверждать, что использование программы (4.3.1) обеспечит

наибольшее значение функции (1) φmax(x) =1972 , т.е. наибольшее производство
	Москва
самостоятельной
Для
продукции. ◄

Таким образом, направленный перебор опорных решений

(последовательное улучшение плана) системы условий задачи привел к

оптима ьной программе использования имеющихся технологических

способов и ре ур ов, с указанием неиспользованных	ресурсов и
максимального объемастудентовпроизводства продукции.

107

Рассмотренный процесс решения можно записать в виде набора симплексных таблиц 1, 2, 3, в которых представлены матрицы систем

уравнений (2.3.1)	(2.3.2)		(2.3.3).
Табл.1	А1	А2	А3	А4	А5	А6		А7	В
	4	3	4	5	1	0		0	208
	2	5	0	2	0	1		0	107
	3	1	2	5	0	0		1	181
-γ	36	14	25	50	0	0		0	0
Табл.2	1	2	2	0	1	работы			27
						0		-1
	4/5	23/5	-4/5	0	0	1		-2/5	МБИ
									173/5
	3/5	1/5	2/5	1	0	0		1	181/5
δ	6	4	5	0	0	0		-10	-1810
Табл.3	1	2	2	0	1	0		-1	.
									27
	0	3	-12/5	0	-4/5	1		2/5	г
									13
	0	-1/5	-4/5	1	-3/5	0	ВПО1/5		20
δ	0	-8	-7	0	-6	0		-4	-1972

Каждый элемент симплексной таблицы имеет экономический смысл.

Например, во 2-ой симплекс таблице при использовании в производстве 1-го
технологического сп с ба, что			2013
		соответствует переменной х1, в векторе А1
элемент а31	=3/5 показывает	насколько	единиц необходимо уменьшить
производство		ЧОУ	4-го технологического способа,
	продукции с использо анием

производствоДля продукциистудентовуменьшится на 8 единиц и на 7 единиц соответственно.

элементы а11=1 и а21 = 4/5 – п казывают с оль о потребуется единиц ресурсов 1-го и 2-го вид в, при этом общее производ тво продукции увеличится на 1 =6 единиц..

Элементы строки оце ок оптимального опорного решения в последней симплексной т блице также имеют экономический смысл. Например, оценки

2= -8 и δ3= -7 векторов А2	и А3, соответствующие переменным х2 и х3 ,
	Москва	использования	2-го и 3-го
показывают, что за о ну единицу времени
самостоятельной		оптимальную	программу,
технологических способов,	не входящих в

В заключение заметим, что в рассмотренном примере возможна проверка результата. Так как, в оптимальной производственной программе х2=0, х3=0, то предположим, что предприятие при производстве продукции не обладало 2-м и

108

3-м технологическими способами. Тогда математическая модель задачи с 1-м и

2-м технологическими способами, соответствующими переменным х1, х4,

примет следующий вид:

х4

grad f(x)

X=(x1,x4)- ?

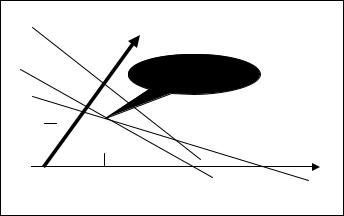
53,5

f(X)

36x1

+50x4

→ max

41,6

Х0=(27;20)

4x1

+5x4

≤

208,

Х2

2x1

+2x4

≤

107,

36,2

3x1

+5x4

≤

181,

20

Х3

x1≥0,

x4≥0.

Х1

Х4

53,5

х1

Решив эту задачу графически

27

52

60,3

работы

убедиться

в

Рис.1

(рис.1),

можно

МБИ

с впадении с ранее полученными

результатами. При этом послед вательн е улучшение производственной

программы при

переходе

от

од ого

опорного

решения

к

другому,

т.е.

Х1= (x1=0,x4=0)

Х2= (x1=0,

x4=181/5)

Х3= (x1=27,

x4=20).соответствует

движению от одной вершины выпуклого множества [Х1 Х2 Х

гХ4] допустимых

решений к соседней вершине по соединяющей их стороне.

ВПО

Для формирования двойств нной задачи к исходной задаче введем вектор

оценки ресурсов Y=(у1, у2, у3) , в котором отражаются условия производства

продукции, т.е.

использование

предприятием

технологических

способов и

ресурсов.

2013

Из матрицы А вект ров условий исходной задачи следует, что для

производства

единицы

продукции

по

1-му

технологическому

способу

ЧОУ

ида, 2-е единицы ресурса 2-го

необходимо затра и ь 4-е единицы ресурса 1-го

вида и 3-и единицы ре урсов 3-го

ида. В двойственных оценках (у1, у2,

у3)

затраты всех вид в ресурс в за единицу времени использования 1-го

технологического способа сос авят 4у1 + 2у2 + 3у3 и при этом будет

произведено 36 единиц продукции. Так как ценность затраченных ресурсов не

меньше ценности произведе

ой продукции, то 4у1 + 2у2 + 3у3 36.

Аналогично рассуждая, получим оценку затрат всех ресурсов за единицу

времени и пользовании 2-го технологического способа 3у1 + 5у2 + у3, которая

Москва

не может бытьсамостоятельнойменьше ценности произведенной продукции, т.е. 3у1 + 5у2 + у3

14, и т.д. по всем технологическим способам.

Оценка всех имеющихся для производства ресурсов равна

208у1 + 107у2 + 181у3.

Определение расчетных оценок ресурсов cводитcя к нахождению вектора

Y = (у1, y2, y3),

студентов

наименьшее

значение

оценки всех

которому соответствует

Для

ресурсов, т.е.

109

						работы
	ψ(Y) = 208y1 + 107y2 +181y3 min						(1д)
	4y1	+2y2	+3y3	≥	36,
	3y1	+5y2	+y3	≥	14,		(2д)
	4y1	+2y2	+2y3	≥	25,
x3 (4y1	5y1		+5y3	≥	50,		x2 + 2xМБИ3 + 5x4 - 181) = 0
	+ 2y3	- 25) = 0		y3	(3x1 +
	y1≥0 y2≥0 y3≥0						(3д)
Решение полученной задачи легко найти с помощью 2-й теоремы
двойственности,	согласно которой			для	оптимальных решений Xo= (х1o, х2o,

х3o, х4o) и Yo=(y1o, y2o, y3o) пары двойственных з д ч необходимо и достаточно выполнение условий

x1о (4y1о + 2y2о + 3y3о - 36) = 0

y1о

(4x1о + 3x2о + 4x3о + 5x4о - 208) = 0

о

самостоятельной

о

о

о

о

о

о

+

о

- 14) = 0

y2

+ 5x2

- 107) = 0

x2

(3y1

+ 5y2

y3

(2x1

+ 2x4

о

о

о

о

о

ВПО

о

о

о

.

x4о(5y1о + 2y2о + 5y3о - 50) = 0

.

т е., х1о>0,

Из решения исходной задачи следует, что Xo=(27;0;0;20),

г

x4о>0. Поэтому

4y1о + 2y2о + 3y3о - 36 =0,

5y1о + 2y2о + 5y3о

- 50 = 0. Т.к. 2x1о

+5x2о

2013

+ 2x4о < 107, то двойственная оценка 2-го ресурса равна нулю, т.е. у2о=0.

Следовательно, приходим к системе уравнений

ЧОУ

4y1о + 2y2о + 3y3о - 36 =0,

5y1о + 2y2о + 5y3о - 50 = 0,

у2о=0,

решением которой будет вектор

Yo=(6, 0, 4) двойственных оценок ресурсов,

симплексной таблицыстудентов3, вект р в условийМоскваА5, А6, А7, соответствующих разрешенным переменным в системе (1.1), Двойственные оценки имеют

доставляющий общей оценке ресурсов наименьшее значение, равное 1972, что соответствует 1-й те реме дв йственности.

Замечание.► Решение двойственной задачи Yo=(6, 0, 4) совпадает с

противоположенными оценками, содержащимися 4-й строке последней

определенный экономический смысл. Например, двойственная оценка третьего ресурса у3 = 4 показывает, что д бавление одной единицы третьего ресурса обеспечит прирост производства продукции на 4 единицы. ◄

В оптимальной производственной программе используются полностью 1-й и 3-й ресурсы. Возможное уменьшение исходных объемов этих ресурсов может оказать влияние на программу использования технологических

способов, ресурсов и на общее количество производимой продукции. С едовательно, акое использование ресурсов создает в производстве «узкие

места». Поэтому желательно иметь некоторый запас таких ресурсов, чтобы

сохранить структуру использования технологических способов и иметь
возможностьДля	для увеличения производства продукции. Ведем вектор

110