Линейная_алгебра_УП_очная_ЭлРес

	Из определения скалярного произведения следуют:
1.	(Г,Х) = 0 Cosφ = 0	φ = π/2 Г┴Х.
	При этом уравнение γ1 x1 + γ2 x2 = 0 задает на плоскости (x1, О, x2) прямую ,
	проходящую через начало координат перпендикулярно вектору Г.
2.	(Г,Х) > 0 0 < Cosφ < 1 0 < φ < π/2.
	При этом неравенство γ1 x1 + γ2 x2 > 0 определяет на плоскости (x1, О, x2)
	полуплоскость с той стороны прямой, заданной соотношением γ1 x1+γ2 x2 = 0,
	куда направлен вектор Г.
3.	(Г,Х) < 0 –1 < Cosφ < 0 π/2 < φ <π.
	При этом неравенство γ1 x1 + γ2		x2 <0 оп еделяет на плоскости (x1, О, x2)
	самостоятельной
	полуплоскость с той стороны прямой, заданнойработысоотношением γ1 x1+γ2 x2 = 0,
							ВПО	МБИ
	куда направлен вектор, противоположенный вектору Г.
4.	(Г,Х)max Cosφ = 1	φ = 0.						.
	При этом векторы Г и Х направле ы в одну сторону.							г
5.	(Г,Х)min Cosφ=–1	φ= π.
	При этом векторы Г и Х направлены в разные стороны.
	Теперь данную линейную функцию (1) можно представить:
	либо в виде	f(x1, x2) = (Г,Х)+ γ0,						(3)
	либо в виде	f(x1, x2) =			Г		ПрГХ + γ ,	(4)

В соотношении (4) величины Г и γ0 являются постоянными. Поэтому

возможные значения функции f(x1, x2) определяются значениями величины –
Москва
ПрГХ (проекции вект ра Х на вектор Г), которая зависит2013	от расположения

точки Х(x1, x2) на мн жестве W. Из соотношения (3) следует, что точка Х(x1, x2)
студентов
принадлежит также прямой линии L, задаваемойЧОУ	ура нением
γ1 x1 + γ2 x2 = f(x1, x2) – γ0.
Абсолютн е значение величины ПрГХ совпадает с		величиной – ρ(0, L),
равной расстоянию от начала координат до	прямой	L. Поэтому, изменяя

положение пря ой L, а вместе с ней и п л жение точки Х (x1, x2), на множестве W, можно изменять расстоя ие от прямой линии L до начала координат, и, согласно (4), изменять знач ние функции f(x1, x2).

Е ли угол между векторами Г и Х острый, то прямая L находится с той стороныДля от прямой, за аваемой уравнением γ1 x1 + γ2 x2 = 0, куда направлен вектор Г, и значение ф нкции f(x1, x2) определяется величиной ρ(0, L), взятой со знаком плюс. Если угол между векторами Г и Х тупой, то прямая L распо ожена с той стороны от прямой, задаваемой уравнением γ1 x1 + γ2 x2 = 0, куда направлен вектор, противоположенный к вектору Г, и значение функции f(x1, x2) определяется величиной ρ(0, L), взятой со знаком минус.

Следовательно, перемещая прямую L вместе с точкой Х (x1, x2) по

41

множеству W			в направлении вектора Г, мы увеличиваем значения функции
f(x1, x2) на множестве						W , а, перемещая в обратном направлении – уменьшаем
значение этой функции на рассматриваемом множестве.
	Наибольшее и наименьшее значения функция дос игает в точках, где
прямая L становиться касательной (опорной) к мн жеству W.
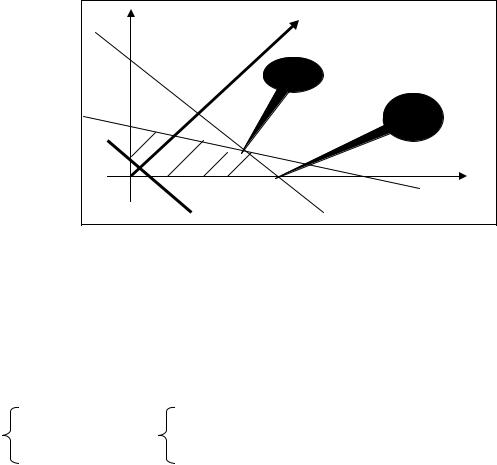
	Пример 1. Найти наибольшее значение функции f(x1, x2)=x1+x2 на
множестве W = { X R2 : fi (x1, x2) 0, i = 1,2,3,4}, где f1 (x1, x2) = x1 + x2 – 4 ,
f2 (x1, x2) = x1 + 3x2 – 6, f3 (x1, x2) = –x1 , f4 (x1, x2) = – x2 .
	▲ Множество W изображено на рис 2.									работы	МБИ
			X2
			4					grad f(X)=Г
								Х01			.
			2							Х02
						W					г
			0			2		4		6	x
						L	Рис.2			ВПО
	Через это множес во перпендикулярно вектору градиента Г = (1,1)
функции f(x1, x2) проводим пр мую линию L, задаваемую уравнением x1+x2 + γ0
= 0. Перемещая прямую линию L в направлении вектора2013градиента до тех пор,
когда она станет касательн й (опорной) к множеству W в каждой точке отрезка
[Х10,Х20] =		W			L.	Координаты		точекЧОУ	Х10,Х20 находятся из решения
соответствующих					и тем ура нений, а именно,
	x1 + x2 = 4 ,					x1 + x2 = 4,
	x1 + 3x2 = 6 ,					x2 = 0.
	Любая точка				Х = αХ10 + (1 – α )Х20, где					α [0,1], данного отрезка будет
являться точкой глобаль ого максимума функции f(x1, x2) на множестве W.■
	Пример 2. (портф ль акций). Инвестор решил вложить 1800 д.е. в
акции двух компаний: в топливно-нефтяную компанию (ТНК) и в компанию по
								Москва
производствусамостокомпьютеровятельно(КПК)й. Стоимости акций этих компаний
соответственно равны						4 д.е. и 8 д.е. При этом обещают, что прибыль от 1 д.е.,
инвестированная в акции ТНК, будет равна 0,115 д.е., а от 1 д.е.,
инвестированной в акции КПК, будет равна 0,12 д.е. за год.
	На рынке продажа продукции компании ТНК более устойчива, чем
				студентов
компании КПК. Поэтому инвестор решает приобрести акций ТНК не меньше,
Для
чем акций КПК.

42

Однако ТНК продает каждому будущему акционеру не более 325 своих

акций, в то время как

КПК продает

свои акции в количествах не менее

60 штук.

Формализуйте условия вложения денег в акции указанных компаний с

учетом того, что инвестор желает получить при эт м наибольшую прибыль.

Изобразите на плоскости множество инвестиционных возможностей.

Найдите инвестиционные возможности, которые соответствуют

желаниям инвестора.

▲ Предположим инвестор приобретет х1 акций ТНК и х2 акций КПК.

Тогда множество инвестиционных возможностей можно записать в виде

2

работы

W ={ X (x1, x2) R

: 0 x1 325, 60

x2,

+ 8х2 1800},

х2

х1

, 4х1

а прибыль от такой сделки в виде функции f(x1, x2) = 0,115(4xМБИ1) + 0,12(8x2).

Математическая постановка задачи: Найти наибольшее значение функции

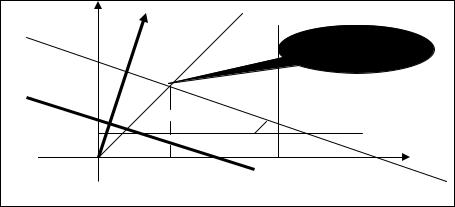
f(x1, x2) = 0,115(4x1) + 0,12(8x2) на м ожестве W. Множество W изображено на

рис. 3.

.

x2

grad f(X)=Г

г

X0(150,150)

225

ВПО

150 -----------

L

W

60

0

325

450

x1

Рис.3

2013

Через это множес во перпендикулярноЧОУ

ектору градиента Г = (0,46;0,96)

функции f(x1, x2) = 0,115(4x1) + 0,12(8x2) проводим прямую линию L,

задаваемую уравнением 0,46x1 + 0,968x2 + γ0 = 0. Перемещая эту прямую в

направлении вект ра градиен а, находим точку Х0(150,150), в которой функция

f(x1, x2) достигает наибольшего значения. ■

Замечание. Графическим методом можно решать задачу линейного

программиров ния,

сли

число переменных – n и число уравнений – m в

системе ограничений этой задачи удовлетворяют соотношению 1 n – m 2.

Для этого необходимо:

Москва

-

самостоятельной

системы

линейных уравнений,

найти методом Га сса общее решение

которая являе ся системой ограничений исходной задачи линейного

программирования;

-

исключив разрешенные переменные

из

полученного

общего решения,

получить системустудентовиз m неравенств с (n–m) переменными;

Для

- из полученного общего решения выразить разрешенные переменные через

43

			работы
свободные переменные и подставить их в целевую функцию, которая станет
функцией (n–m) свободных переменных;
- решить	графическим	методом	полученную	задачу	линейного
программирования с (n–m)		свободными	переменными, с ограничениями в
3x1 + 2x2 – x3 + 4x 4 = 3,				МБИ
виде m неравенствами, а также с ограничениями на знак переменных;

- найденные свободные переменные подставить в о щее решение, вычислить значения разрешенных переменных и записать оптимальное решение исходной задачи.

Пример 4. Найти наименьшее значение функции f(X) = 4x1 – 2x2 + x3 – x4

на множестве W, заданном системой уравнений:

самостоятельной0

ВПО

x1

– x2

+ 4x3

– 2x4

= 2,

хj

0,

j = 1, 2, 3, 4.

г

▲

Разрешим

систему

огра ичений

относительно

первых двух

переме ых и получим общее решение системы

А1

А2

А3

А4

В

2013

.

1

–1

4

–2

2

уравнений в виде

х1 + 7/5 x = 7/5,

3

2

–1

4

3

ЧОУ

x2 – 1 /5 x

+ 2 x4 = –3/5,

1

–1

4

–2

2

из которого следует, что

0

5

– 13

10

–3

х1 = –7/5 x3 + 7/5,

1

0

1,4

0

1,4

0

1

– 2,6

2

–0,6

x2 = 13/5 x3 – 2 x4 – 3/5.

Исключаем разрешенные переменные из общего решения

получаем систему

Москва

неравенств с переменными х3 и х4. Подставляем переменные х1 и х2,

выраженные через переменные х3

и х4 в целевую функцию. Получаем задачу

дстуентов

линейного программирования с двумя переменными х3 и х4

и с ограничениями

в виде неравенств, а именно, найти наименьшее значение целевой функции

f(X) = – 9,8x3 + 3x4 +6,8 на мн жестве,

х3

≤1,

заданном систем й неравенств:

– 2,6 x3

+ 2 x4 ≤ –0,6,

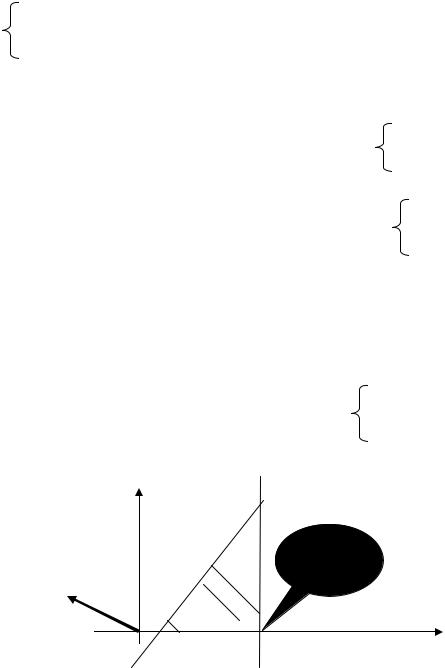
Решаем задачу графическим ме одом.

х3 ≥0,

х4

≥0.

Для

х4

L

0

=1,

х3

grad f(X)=(-9,8;3)

х4 =0

W

0

0,27

1

х3

Рис.4

0

=1, х4

0

=0 подставляем в выражения для

Найденные значения переменных х3

44

первых двух переменных и выписываем оптимальное решение исходной задачи Х0=(0,2,1,0) и соответствующее ему значение целевой функции f(X0) = –3. ■

При решении экономических задач переменная хj, j = 1, 2, …, n, соответствует ресурсу j-го вида (сырье, труд, деньги, время и т.п.). Неравенства

fi (X) 0,	i I;	fi (X)=0, i M\I хj 0, j=1,2, … , n задают ограничения на
использование		этих ресурсов. Функция f (X) определяет цель (качество)
использования ресурсов.
На этапе развития методов решения т ких з д ч каждое решение системы

ограничений на использование ресурсов называли планом (или программой).

План (программа), доставляющий экстремальное значение целевой функции,
						работы
называли оптимальным. Поэтому направление науки, занимающееся
постановкой таких задач и разработкой						методов	нахожденияМБИ			оптимальных
						ВПО
	функциисамостоятельнойf(X) в каком направлении и до какого положения необходимо
решений, назвали математическим пр граммированием (планированием).
									.
	В зависимости от вида целевой фу кции и вида функций в ограничениях
таких задачах									г
			различают направле ия математического про раммирования:
								2013
линейное, нелинейное, выпуклое, дискретное, стохастическое и т.п. Мы начнем
изучение		математического программирования с					наиболее разработанных и
					ЧОУ
доступных задач – задач линейного программирования.
Ответьте на вопросы
1.	Дайте определение замкну ого множества.
2.	Какие из множеств			[a,b], [a, b), (–∞, b], (a, b), (a, +∞) являются замкнутыми,
	а какие не являются замкнутыми?				Москва
3.			студентов
	Дайте определение предельной точки множества. Укажите множество всех
	предельных точек для множеств из пункта 2.
4.	Какие из множе тв п.2 я ляются ограниченными, а какие не являются
	ограниченными?
5.	Дайте определение градиен а функции не кольких переменных.
6.	Напишите фор улу для нахождения расстояния от начала координат до
	прямой линии, зада			ой урав ением Ax+By+C=0.
7.	Когда прям я линия явля тся опорной к некоторому множеству?
8.	При	пои ке	графическим методом			глобального минимума линейной
	Для
	перемещать прям ю f(X)=0 относительно градиента этой функции?
9.	Какие задачи линейного программирования можно решать графическим
	методом?
10. айте		определения общего решения системы линейных уравнений,
	разрешенных переменных и свободных переменных.

11.Опишите последовательность решения задачи линейного программирования

45

		работы
	с m переменными и n ограничениями в виде линейных уравнений, если
	1 n–m 2.
12.Почему данная дисциплина имеет название – математическое
	программирование?		МБИ
Решите самостоятельно
	Задача 1. В условиях примера 3 через год условия инвестирования
изменились, а именно:
1.	Прибыль от 1 д.е., инвестированной в акции ТНК стала в два раза больше, а
по акциям КПК прибыль осталась на прежнем у овне.
2.	самостоятельной
	Стоимость акции ТНК возросла в 1,5 раза, а цена акций КПК упала на 20%.

Инвестор решил купить акций ТНК как минимум в два с лишним раза больше,
			ВПО
чем акций КПК. Дайте ответы на вопросы, поставленные в примере 3.
					.
		ЧОУ		2013	г
Для	студентов	Москва

46

(4)

xj ≥ 0,

j J N=(1, 2, …, n}

работы

2.2. Общая задача линейного программирования

Рассмотрим математическую постановку задачи, в которой функции f(X)

и fi(X), i = 1, 2, …, m, являются линейными.

Найти наибольшее или наименьшее значение функции

n

(1)

f(X)

= γj xj + γ0 , при условии, что

j 1

n

(2)

a ij

xj

≤ bi , i I M={1,2,…,m},

j 1

n

(3)

a ij

xj

= bi , i M \ I,

программирования на

максимум

Замечаниесамостоятельной. В за ачах линейного

j 1

ВПО

задачейМБИ

Задача

(1) – (4)

называется

общей

линейного

программирования; функция f(X)

–

целевой

функцией

или

функцией

качества; система

линейных неравенств

(2) и линейных

.

уравнений (3) –

системой ограничения,

а нераве ства

(4) –

г

условием неотрицательности

переменных.

2013

К

частным

случаям общей

задачи

линейного программирования

ЧОУ

относятся: каноническая задача и стандартная задача.

1. Каноническая задача лин йного программирования (КЗЛП), когда I = Ø, J = N, bi ≥ 0, i M и находи ся наибольшее или наименьшее значение функции

	n
	f(X) = γj xj + γ0 , при условии, что
	j 1		Москва
	n
	a ij xj	= bi , i =1,2,…,m,
	j 1
	xj ≥ 0,	j=1, 2, …, n.
		студентов
2. Задача линейного программир вания стандартного вида, когда J=N, I=M
и находится наиб льшее или наименьшее значение функции
	n
	f(X) = γj xj + γ0 , при условии, что
	j 1
	n
	a ij xj	≤ bi , i =1,2,…,m,
Для	j 1
	xj ≥ 0,	j = 1, 2, …, n.
(минимум) находятся значения координат вектора Х = (х1, …, хj, …, хn), при
которых достигае ся наибольшее(наименьшее) значение целевой функции.
	Определение. Вектор α = (α1, …, αn) называется допустимым решением

задачи линейного программирования (1)–(4), если он является решением ограничений (2) – (3) и удовлетворяет условию (4).

Множество всех допустимых решений задачи (1)–(4) обозначим через W.

47

	работы
Определение. Допустимое решение α0	= (α10, …, αn0) задачи линейного

программирования (1) – (4) на максимум (или минимум) целевой функции f(X) называется оптимальным решением, если для всех допустимых решений этой

задачи выполняется неравенство f(α0) ≥ f(α)	( или f(α0) ≤ f(α) ).
0	МБИ

Замечание. Оптимальное решение задачи линейн го программирования

(1) – (4) является точкой глобального экстремума функции f(X) на множестве допустимых решений W.

Определение. Решить задачу линейного программирования это, значит, найти оптимальное решение этой задачи, или доказать, что оптимального решения этой задачи не существует.

Простейшие свойства задач лине ного программирования

1 . Оптимальное решение задачи линейного программирования не изменится, если целевую функцию помножить на любое положительное число, либо

прибавить к целевой функции любое число.

Доказательство

этого

утверждения

можно провести самостоятельно,

используя

графический

метод

решения

.

линейного

задачи

программирования.

г

20. Рассмотрим общую задачу лин йного программированияВПО

:

n

2013

(1)

f(X) = γj xj + γ0 (max),

n

j 1

(2)

a ij

xj

≤ bi , i I M={1,2,…,m},

j 1

n

(3)

a ij

xj

= bi , i I \ M={1,2,…,m},

j 1

ЧОУ

(4)

xj

≥ 0,

j J N=(1, 2, …, n}

Умножив целевую функцию (1) на (–1), рассмотрим новую задачу, а

именно,

(1’ )

n

f1(X) = – γj

xj – γ0 = – f(X)

(min),

n

j 1

(2’ )

a ij

xj

≤ bi , I I M={1,2,…,m},

j 1

(3’ )

n

xj

= bi , i I \ M={1,2,…,m},

a ij

’

j 1

Москва

самостоятельной

(4 )

xj ≥ 0,

j J N=(1, 2, …, n}.

Вектор α0 является оптимальным решением задачи (1) – (4) на

максимум тогда и

олько тогда,

когда

α0 является оптимальным решением

задачи (1’)–(4’) на минимум.

▲ Необходимость. Пусть W есть множество допустимых решений

задачи (1)–(4)

студентов

и задачи

(1’)–(4’), а вектор α0 является оптимальным решением

Для

на максимум. Тогда, по определению глобального максимума,

задачи (1)–(4)

48

выполняется неравенство f(α0) ≥ f(α) для любого вектора α W. Умножив последнее неравенство на минус единицу, получим новое неравенство –f(α0) ≤ – f(α) и с учетом обозначения целевой функции задачи (1’)–(4’) имеем f1(α0) ≤ f1(α) для любого вектора α W. Откуда, по определению глобального минимума функции f1(X), вектор α0 является птимальным решением задачи (1’)–(4’) на минимум. Таким образом, нео ходимость доказана. Для доказательства достаточности следует провести рассуждения в обратной последовательности.■

Замечание. В дальнейшем будем ассматривать решение задач

линейного программирования только на минимум, так как задача на максимум
					работы
может быть сведена к соответствующей задаче на минимум.
							МБИ
Ответьте на вопросы
1.	Опишите общую задачу линей ого программирования.
2.	Опишите каноническую задачу ли ей ого программирования.
3.								.
	Опишите задачу линейного программирования стандартного вида.
4.	Дайте	определение	допустимого		решения			г	линейного
							задачи
	программирования.				ВПО
5.
	Дайте определение оптимального решения задачи линейного
	программирования.
6.	Как	понимать	высказывание:		«решить		задачу		линейного
	программирования»?					2013
7.
	Какие действия с целев й функцией не влияют на результат решения задачи
	линейного программирования?			ЧОУ
8.
	Какие действия целевой функцией задачи линейного программирования
	приводят к тому, что оптимальн е решение задачи на максимум совпадает с
	оптимальным решением т й же задачи только на минимум?
9.	Дайте доказательство у верждения, к т р е является правильным ответом
	на вопрос в п.7.			Москва
	Для	самостоятельной
		студентов

49

2. 3. Примеры задач линейного программирования Задача планирования работы предприятия. Предприятие располагает

m видами ресурсов и имеет возможность выпуска ь однородную продукцию,

используя n различных технологических способов.
За единицу времени	использования j-го техн логического способа
(j = 1,2,…,n) расходуется	aij	единиц i-го ресурса, запас которого равен bi
(i = 1,2,…,m), и выпускается cj		единиц продукции.
Требуется сформировать такой план р боты предприятия, чтобы выпуск
продукции был наибольшим, а		расход каждого вида ресурса		не превосходил
его запаса.		работы
Обозначим через xj	–			технологического
		время использования j-го
способа. Тогда:			МБИ

X = (x1, … ,xj, … , xn ) – план (пр грамма) работы предприятия, в котором,

естественно, что все переменные е отрицательны, т.е. xj							≥ 0, j = 1, 2, …, n;
n								.
cj xj	– планируемое к выпуску количество продукции;
								г
j 1
aij xj –									j-го
	количество i-го ресурса, которое расходуется при использовании
технологического способа;				ВПО
n
aij	xj – общий расход	i-го ресурса при выполнении всей программы							не
j 1
					n
должен превышать его запасов на предприятии, т.е. aij xj ≤ bi.
Таким образ м, приходим					j 1	2013
			к матем тической				постановке задачи
			ЧОУ
			Москва
	самостоятельной
планирования рабо ы предприятия в виде задачи линейного программирования
веществ не меньшестудентовдневной нормы.
		n
на максимум:		f(X) = cj xj (max),
		j 1
		n
		aij xj	≤ bi. i=1,2,…,m;

xj j1≥ 0, j=1,2,…,n.

З д ча пл нирования рационального питания. В продаже имеется n

видов продуктов. В динице продукта j-го вида (j = 1, 2, …, n) содержится aij единицДля i-го химического элемента. (i = 1,2,…,m), необходимого для организма. Известна bi – дневная норма потребления i-го химического вещества и цена cj единицы j-го продук а.

Необходимо сос авить рацион так, чтобы затраты на покупку продукта были минимальными при условии, что в продуктах содержится химических

Обозначим через xj количество единиц j-го продукта в дневном

50