Лабораторная работа 13 Решение нелинейных уравнений

Цель работы: научиться разрабатывать и отлаживать программы для на­хождения корней нелинейных уравнений численными методами

Пусть задано уравнение f(x)=0 и интервал [a,b], где функция f(x) непрерывна и имеет разные знаки на концах интервала.

Алгоритм нахождения корня на интервале методом половинного деле­ния (бисекции) сводится к следующей схеме:

1) вычисляется середина интервала c = (a+b)/2;

2) если |f(c)| < e, где e= 10^-3 - 10^-5 определяет погрешность вы­числений, то c будет являться приближенным значением корня уравнения и выводится как результат расчетов;

3) если |f(c)| > e, то проверяются знаки функций f(a) и f(c) на концах отрезка [a,c], для чего вычисляется их произведение. Если f(a)f(c)<0, то функции будут иметь противоположные знаки и корень находится на отрезке [a,c]. В этом случае интервал [a,b] заменяется отрезком [a,c], для чего присвоим b=c;

4) иначе, если f(a)f(c)>0, корень уравнения находится на отрезке [c,b] и в рас- четах интервал [a,b] заменяется на [c,b], для чего прис­воим a =c;

5) вычисления по схеме п.1-п.4 повторяются в итерационном цикле до тех пор, пока не выполнится условие п.2 - |f(c)|< e.

В случае метода хорд схема алгоритма расчета корня уравнения ос­тается прежней за исключением п.1, в котором используется формула

c=(a f(b)-b f(a))/(f(b)-f(a)).

Для исключения зацикливания следует правильно определять начальный интервал [a,b], чтобы выполнялось условие f(a)f(b)<0. Структурная схема алгоритма для метода половинного деления приведена на рис.13.

Задание (программа_13)

Найти корень уравнения f(x)=0 на интервале [a,b] с точностью e=0.001.

1. x - 2e^-x - = 0. 2. x² - ln(x+1) + sin x -2 = 0.

3. 5x - e^x -2x = 0. 4. 2x lg x - 3 = 0.

5. 2^x - 3x - 2 = 0. 6. 0,5 + cos x - 2x sin x = 0.

7. sin x + x - 3 = 0. 8. x e^x – 2 x² - 1 = 0.

9. + 2x - 3 = 0. 10. 2 ln(x+1) - x + 1 = 0.

11. tg x - e^x+1 = 0. 12. 2 ln(x+1) + arctg x -3 = 0.

13. x³ - 2x² - 4 = 0. 14. 5x² - 2x ln x-7 = 0.

15. 2 - 3 sin x = 5. 16. 2x³ - 3x² - 4 = 0.

17. 4x - sin2x -3 = 0. 18. 2x sin² x-3= 0.

19. 2 ln(x+1)-3 sin2x = 4. 20. x³ + 3x + 2 = 0.

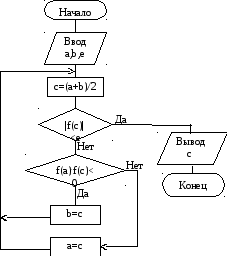
Рис.13. Схема алгоритма решения нелинейного уравнения

Лабораторная работа 14 Вычисление приближенного значения определенного интеграла

Цель раборы: научиться разрабатывать и отлаживать программы для вычисления определенных интегралов численными методами прямоугольников и трацеций

Приближенное значение определенного интеграла вычисляется как сумма площадей N прямоугольников, построенных на интервале интегрирования [a,b]. Интервал [a,b] разбивается на N равных частей длиной h = (b-a)/N, на каждой из которых строится прямоугольник с высотой, рав­ной значению функции f(x_i) в центре участка с координатой

x_i = a+(i-0.5)h, где i=1,2,...,N

Формула прямоугольников для приближенного вычисления значения интеграла будет иметь вид

.

В методе трапеций весь интервал [a,b] разбивается на N равных частей длиной h=(b-a)/N, на каждой из которых строится трапеция. Приближенное значение ин- теграла определяется суммой площадей этих трапеций

,

где x_i =a+i* h .

Разработать программу для вы­числения значения определенного интеграла на интервале [a,b] (a, b подобрать самостоятельно) численными методами прямоугольников и трапеций [8, 9] для следующих вариантов:

1. 2. 3.

4. 5. 6.

7. 8. 9.

10. 11. 12.

13. 14. 15.

16. 17. 18.

19. 20.

Интервал интегрирования разбить равномерно на N>50 частей.