Понятие о фрактальной размерности.

Ломанной линии:

N – количество отрезков, размером а.

D – «степень изгибания»

N=(1/a)D; S=N*a ; S=(1/a)D-1

Кривая Коха

1) L=1

2) N=4 L=1/3 S(4)=4/3

3. N=16 L=1/9 S(16)=16/9

Фрактальная размерность:

D=lg 4 / lg 3=1.26…

Фрактальная размерность множества

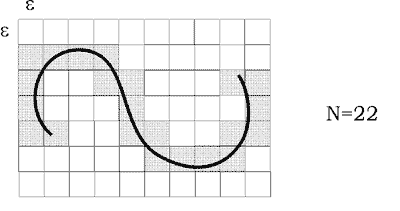
Объем фрактала в своем пространстве вложения всегда равен нулю. Он, однако, может быть отличен от нуля в пространстве меньшей размерности. Чтобы определить размерность этого пространства D, разобьем все n-мерное пространство на малые кубики с длиной ребра ε и объемом εⁿ — рис. 1. Пусть N(ε) — минимальное число кубиков, которые в совокупности полностью покрывают фрактальное множество, тогда по определению

(1)

Эту величину обычно называют хаусдорфовой или фрактальной размерностью.

Рис. 1. Как найти фрактальную размерность?

Существование этого предела означает конечность объема фрактала в D-мерном пространстве: при малом ε

N(ε)≈ Vε^–^D ,

(2)

где V = const. Таким образом, N(ε) есть не что иное, как число D-мерных кубиков, покрывающих в D-мерном пространстве объем V. Поскольку покрывающие фрактал n-мерные кубики могут оказаться почти пустыми

D<n

(3)

и в отличие от привычной размерности D может быть дробной величиной, каковой она чаще всего и является для фрактальных множеств.

Очевидно, что для обычных множеств это определение приводит к хорошо известным результатам. Так для множества N изолированных точек имеем N(ε) = N и поэтому

(4)

Для отрезка достаточно гладкой линии длины L: N(ε) = L/ε и поэтому D = 1. Для площадки S двумерной поверхности: N(ε) = S/ε² и D = 2 и т.д..

Рекурсивный алгоритм построения конструктивных фракталов.

Треугольник Серпинского — фрактал, один из двумерных аналогов множества Кантора предложенный польским математиком Серпинским в 1915 году. Также известен как «решётка» или «салфетка» Серпинского.

Построение

Берётся сплошной равносторонний треугольник, на первом шаге из центра удаляется внутренность срединного треугольника. На втором шаге удаляется три срединных треугольника из трёх оставшихся

треугольников и т. д. После бесконечного повторения этой процедуры, от сплошного треугольника остаётся подмножество — треугольник Серпинского.

Построение треугольника Серпинского

Треугольник Серпинского можно также получить по следующему алгоритму:

1. Взять три точки на плоскости, и нарисовать треугольник.

2. Случайно выбрать любую точку внутри треугольника, и продвинуться на половину расстояния от этой точки к любой из трёх вершин треугольника.

3. Отметить текущую позицию.

4. Повторить с шага 2.

Свойства

• Треугольник Серпинского замкнут.

• Треугольник Серпинского имеет топологическую размерность 1.

• имеет промежуточную (т.е. не целую) Хаусдорфову размерность 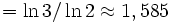. В частности,

  • имеет нулевую меру Лебега.

• Треугольник Серпинского получается из Треугольника Паскаля рассмотрением чётных чисел как точек, принадлежащих треугольнику Серпинского и нечётных - как не принадлежащих.

10