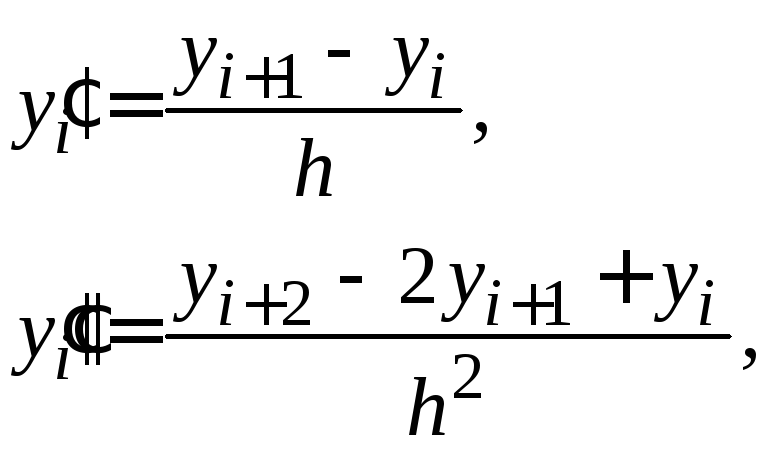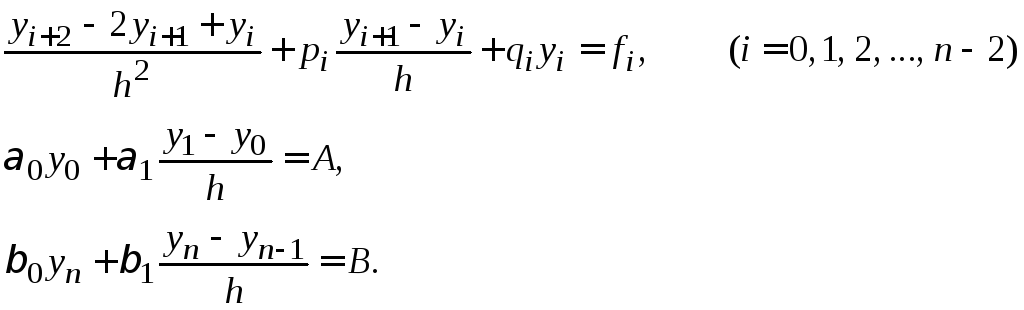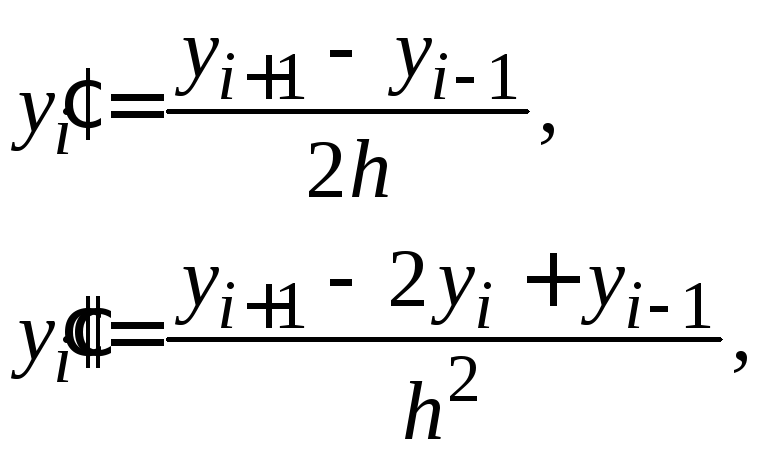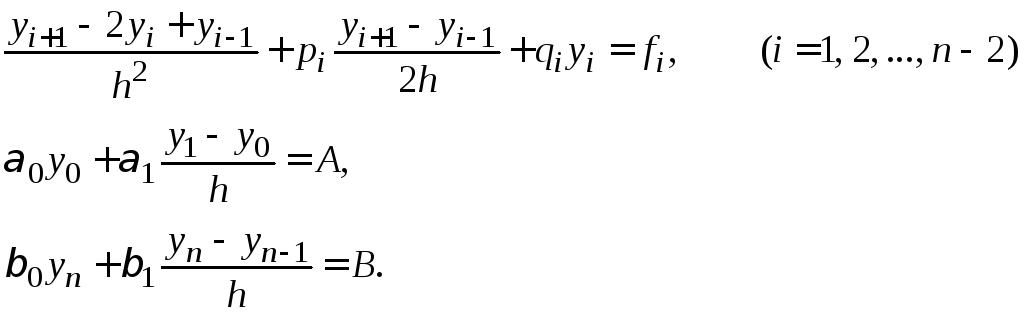- •Математическое моделирование и вычислительный эксперимент.
- •Виды погрешностей.
- •2. Приближенное решение нелинейных уравнений
- •3.Численное решение систем нелинейных уравнений.
- •4.Численные методы решения систем линейных алгебраических уравнений (слау).
- •5. Численное интегрирование. Квадратурные формулы Ньютона–Котеса. Формула трапеций, формула Симпсона. Погрешность квадратурных формул. Интегрирование с помощью степенных рядов. Метод Монте-Карло.
- •6. Численное дифференцирование.
- •7. Интерполирование функций.
- •8. Численное решение задачи Коши для дифференциальных уравнений.
- •9. Краевые задачи для обыкновенных дифференциальных уравнений.
- •13. Комбинаторные объекты и комбинаторные числа
- •14. Рекуррентные соотношения
- •15. Булевы функции. Представление булевых функций полиномами Жегалкина.
- •17. Множества.
- •Операции над множествами
- •Свойства отношений
- •Примеры отношений эквивалентности
- •18. Графы.
- •Эйлеровы графы.
- •5 Красок
- •19. Алгоритмы на графах. Алгоритмы на графах.
- •Задача о кратчайших путях
- •Различные алгоритмы на графах
- •Перебор с возвратами
- •Методы сокращения перебора: эвристики, метод ветвей и границ, динамическое программирование.
- •20. Деревья.
- •21. Проблема разрешимости в алгебре высказываний.
- •24. Понятие о компьютерном математическом моделировании. Этапы и цели. Классификация математических моделей. Моделирование физических процессов.
- •25. Имитационное моделирование.
- •26. Моделирование фрактальных объектов. Моделирование фрактальных объектов.
- •Самоподобные множества с необычными свойствами в математике
- •Рекурсивная процедура получения фрактальных кривых
- •Фракталы как неподвижные точки сжимающих отображений
- •Фракталы в комплексной динамике
- •Стохастические фракталы
- •Применение фракталов
- •Конструктивные, алгебраические и стохастические фракталы.
- •Понятие о фрактальной размерности.
- •Рекурсивный алгоритм построения конструктивных фракталов.
- •Построение
- •Свойства
8. Численное решение задачи Коши для дифференциальных уравнений.
Постановка задачи Коши
Рассмотрим
обыкновенное дифференциальное уравнение
первого порядка:
![]() .
(1.1)
.
(1.1)
Основная
задача, связанная с этим уравнением –
задача Коши состоит в следующем: найти
решение уравнения (1.1) в виде функции
![]() удовлетворяющей начальному условию:
удовлетворяющей начальному условию:![]() .
(1.2)
.
(1.2)
Геометрически
это означает, что требуется найти
интегральную кривую
![]() проходящую
через заданную точку
проходящую
через заданную точку![]() при
выполнения равенства (1.1). Существование
и единственность решения уравнения
(1.1) обеспечивается следующей теоремой.
при
выполнения равенства (1.1). Существование
и единственность решения уравнения
(1.1) обеспечивается следующей теоремой.
Теорема Пикара: Если функция f определена и непрерывна в некоторой области G, определённой неравенствами:
![]() (1.3)
(1.3)
и
удовлетворяет в этой области условию
Липшица по у:
![]() ,
то на некотором отрезке
,
то на некотором отрезке![]() ,
гдеh
– положительное число, существует, и
притом только одно, решение
,
гдеh
– положительное число, существует, и
притом только одно, решение
![]() уравнения (1.1), удовлетворяющее начальному
условию
уравнения (1.1), удовлетворяющее начальному
условию![]() .
.
Здесь М – постоянная (константа Липшица), зависящая в общем случае от а и b.
Если
f(x,
y)
имеет ограниченную в G
производную
![]() ,
то при
,
то при![]() можно принять
можно принять![]() .
.
В классическом анализе разработаны методы нахождения решений дифференциальных уравнений через элементарные (или специальные) функции. На практике эти методы очень часто оказываются либо совсем беспомощными, либо их использование требует трудных вычислений и времени.
Для
решения практических задач созданы
методы приближённого решения
дифференциальных уравнений. Пусть
требуется на отрезке
![]() [х0,
х00+Н]
найти решение уравнения (1.1) при начальном
условии (1.2).
[х0,
х00+Н]
найти решение уравнения (1.1) при начальном
условии (1.2).
Разобьём
отрезок на п
равных частей точками:
![]() ,
где
,
где
![]() .
.
Численное
решение дифференциального уравнения
(1.1) заключается в том, что значение
искомой функции
![]() вычисляется
в каждой точке
вычисляется
в каждой точке
![]()
![]() .
При этом, как правило, для вычисления
значения
.
При этом, как правило, для вычисления
значения![]() используется уже вычисленное значение
используется уже вычисленное значение![]() .
.
Для решения задачи Коши для обыкновенных дифференциальных уравнений существуют различные методы:
1. Аналитические методы, применение которых дает решение дифференциального уравнения в виде аналитического выражения.
2. Графические методы, дающие приближенное решение в виде графиков.
3. Численные методы (табличные), при использовании которых искомая функция получается в виде таблицы.
Ниже рассматриваются относящиеся к указанным группам некоторые методы решения обыкновенных дифференциальных уравнений первого порядка вида (1.1).
Метод последовательных приближений
Рассмотрим
задачу Коши для дифференциального
уравнения первого порядка
![]() с начальным условием
с начальным условием![]() .
.
Метод
последовательных приближений состоит
в том, что решение
![]() ,
получают как предел последовательности
функций
,
получают как предел последовательности
функций![]() ,
которые находятся по рекурсивной формуле
,
которые находятся по рекурсивной формуле
![]() .
(1.4)
.
(1.4)
Если
правая часть
![]() в некотором замкнутом прямоугольнике
в некотором замкнутом прямоугольнике![]() ,
содержащем множество точек
,
содержащем множество точек![]() ,
для которых выполняются условия
,
для которых выполняются условия![]() удовлетворяет условию Липшица по
удовлетворяет условию Липшица по![]() :
:
![]() ,
,
то
независимо от выбора начальной функции
последовательные приближения
![]() сходятся на некотором отрезке
сходятся на некотором отрезке![]() к точному решению задачи Коши.
к точному решению задачи Коши.
Если
![]() непрерывна в области
непрерывна в области![]() ,
то оценка погрешности приближенного
решения
,
то оценка погрешности приближенного
решения
![]() на отрезке
на отрезке
![]() дается неравенством:
дается неравенством:
![]() ,
(1.5)
,
(1.5)
где
![]() ,
а число
,
а число
![]() определяется из условия:
определяется из условия:
![]() .
.
Метод Эйлера
Рассмотрим
дифференциальное уравнение
![]() с начальным условием
с начальным условием![]() .
.
Выбрав
достаточно малый шаг
![]() ,
построим систему равноотстоящих узлов
,
построим систему равноотстоящих узлов![]() ,
(
,
(![]() ).
).
Приближенные
значения
![]() по
методу Эйлера вычисляются последовательно
по формулам:
по
методу Эйлера вычисляются последовательно
по формулам:
![]() (
(![]() )
)
При оценке погрешности обычно используется двойной пересчет.
Если
![]() – вычисленное значение
– вычисленное значение![]() с шагом
с шагом![]() ,
а
,
а![]() – соответствующее узловое значение,
полученное с шагомh,
то для ориентировочной оценки погрешности
последнего значения можно использовать
формулу:
– соответствующее узловое значение,
полученное с шагомh,
то для ориентировочной оценки погрешности
последнего значения можно использовать
формулу:
![]()
Метод Эйлера–Коши
Метод Эйлера–Коши является модификацией метода Эйлера. Вычисления табличных значений решения и оценка погрешности проводятся по следующим формулам.
![]() ,
,
![]() ,
,
![]() ,
,
где
![]() – точное
значение решения в узле
– точное
значение решения в узле![]() ,
,![]() ,
,![]() –
приближенные значения решения в узле
–
приближенные значения решения в узле![]() с шагом
с шагом![]() – соответственно.
– соответственно.
Метод Рунге–Кутта четвертого порядка
Рассмотрим метод Рунге–Кутта четвёртого порядка для нахождения численного решения уравнения (1.1) с начальным условием (1.2).
Пусть
![]() является начальным условием (при
является начальным условием (при![]() ),
либо получено как результат предыдущего
шага. Для получения следующего значения
),
либо получено как результат предыдущего
шага. Для получения следующего значения![]() вначале вычисляются числа:
вначале вычисляются числа:
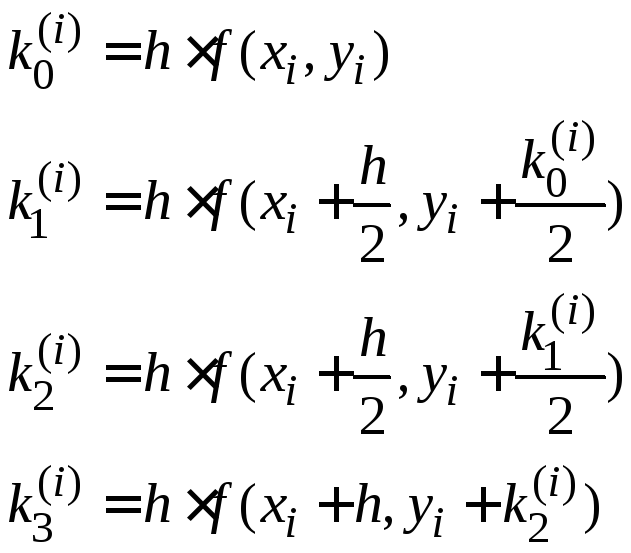 ,
(1.6)
,
(1.6)
где h – шаг интегрирования.
Затем
вычисляют:
![]() .
.
Новое значение функции вычисляется по формуле:
![]() .
(1.7)
.
(1.7)
Метод Рунге–Кутта четвертого порядка является методом повышенной точности. На практике для контроля точности этого метода используется двойной счет пересчет.
Если
![]() –
вычисленное значение
–
вычисленное значение![]() с
шагом
с
шагом![]() ,
а
,
а![]() –
соответствующее узловое значение,
полученное с шагомh,
–
соответствующее узловое значение,
полученное с шагомh,
то
для приближенной оценки погрешности
значения
![]() можно использовать формулу:
можно использовать формулу:
![]()
Многошаговые методы. Метод Адамса. Методы прогноза–коррекции
В
многошаговых методах для вычисления
![]() требуется не одно предыдущее значение
требуется не одно предыдущее значение![]() ,
а несколько. Так, дляk-шагового
метода требуются значения:
,
а несколько. Так, дляk-шагового
метода требуются значения:
![]() .
.
Метод
Адамса является примером многошаговых
методов решения обыкновенных
дифференциальных уравнений. Простейший
случай метода Адамса получается при
![]() и совпадает с рассмотренным ранее
методом Эйлера первого порядка. В
практических расчетах чаще используется
метод Адамса, имеющий четвертый порядок
точности и использующий на каждом шаге
результаты предыдущих четырех значений
приближенного решения. Именно этот
метод называют обычно методом Адамса.
Рассмотрим расчетные формулы для данного
метода.
и совпадает с рассмотренным ранее
методом Эйлера первого порядка. В
практических расчетах чаще используется
метод Адамса, имеющий четвертый порядок
точности и использующий на каждом шаге
результаты предыдущих четырех значений
приближенного решения. Именно этот
метод называют обычно методом Адамса.
Рассмотрим расчетные формулы для данного
метода.
Пусть
вычислены значения
![]() в четырех последовательных узлах
в четырех последовательных узлах
![]() .
Формула для вычисления значения
.
Формула для вычисления значения
![]() по методу Адамса имеет вид:
по методу Адамса имеет вид:
![]() .
(1.8)
.
(1.8)
Первые четыре значения для начала вычисления значений решения по методу Адамса получаются любым другим методом соответствующей точности, например, методом Рунге-Кутта четвертого порядка.
Сравнивая
метод Адамса с методом Рунге-Кутта той
же точности, следует отметить его
экономичность, так как он требует при
вычислении лишь одного значения правой
части на каждом шаге, а метод Рунге–Кутта
– четырех. Но метод Адамса неудобен
тем, что невозможно начать счет только
по известному значению
![]() ,
надо вычислить еще
,
надо вычислить еще![]() каким-либо другим способом (например,
методом Рунге–Кутта), что существенно
усложняет алгоритм. Кроме того, метод
Адамса не позволяет (без усложнения
формул) изменить шагh
в процессе
счета.
каким-либо другим способом (например,
методом Рунге–Кутта), что существенно
усложняет алгоритм. Кроме того, метод
Адамса не позволяет (без усложнения
формул) изменить шагh
в процессе
счета.
Существует еще одно семейство многошаговых методов, которые используют неявные схемы, - методы прогноза и коррекции. Суть этих методов состоит в следующем.
На каждом шаге вводятся два этапа, использующих многошаговые методы:
1)
с помощью явного метода (прогноза) по
известным значениям функции в предыдущих
узлах находятся начальное приближение
![]() в новом узле;
в новом узле;
2)
используя неявный метод (корректор), в
результате итераций находятся приближения
![]()
Один из вариантов метода прогноза и коррекции может быть получен на основе метода Адамса четвертого порядка. Для этого используются следующие расчетные формулы.
На этапе прогноза используется рассмотренная выше формула (1.8), а на этапе коррекции:
![]() (1.9)
(1.9)
Явная
схема (1.8) используется на каждом шаге
один раз, а с помощью неявной схемы (1.9)
строится итерационный процесс вычисления
![]() .
.
Итерации можно прекратить, если две последовательные итерации дают практически одинаковые результаты. На практике, если метод k -шаговый, то итераций должно быть не более k. Дальнейшее увеличение числа итераций порядок точности не увеличивает. Если точность мала, то надо менять шаг, что в многошаговых методах затруднительно.
Постановка краевой задачи для обыкновенного дифференциального уравнения
Пусть дано дифференциальное уравнение второго порядка
|
|
(1.10) |
Двухточечная краевая задача для уравнения (1.10) ставится следующим образом.
Найти
функцию
![]() ,
которая внутри отрезка
,
которая внутри отрезка![]() удовлетворяет
уравнению (110), а на концах отрезка —
краевым условиям
удовлетворяет
уравнению (110), а на концах отрезка —
краевым условиям
|
|
(1.11) |
Рассмотрим случай, когда уравнение (1.10) и граничные условия (1.11) линейны. В этом случае дифференциальное уравнение и краевые условия записываются так:
|
|
(1.12) |
|
|
(1.13) |
где
![]() –
известные непрерывные на отрезке
–
известные непрерывные на отрезке![]() функции,
функции,![]() –
заданные постоянные, причем
–
заданные постоянные, причем![]() и
и![]() .
.
Приближенное решение обыкновенных дифференциальных уравнений методом конечных разностей
Данный метод заключается в следующем.
Разбиваем
отрезок
![]() наn
равных частей с шагом
наn
равных частей с шагом
![]() и получаем точки
и получаем точки![]() ,
в которых требуется найти искомые
значения
,
в которых требуется найти искомые
значения![]() .
.
Введем обозначения:
![]()
Заменим
приближенно в каждом внутреннем узле
производные
![]() конечно-разностными схемами:
конечно-разностными схемами:
|
|
(1.14) |
а на концах отрезка положим:
|
|
(1.15) |
Используя формулы (1.14)–(1.15), приближенно заменим уравнения (1.12)-(1.13) системой уравнений:
|
|
(1.16) |
Получим линейную алгебраическую систему, содержащую n+1 уравнение с n+1 неизвестным. Решив данную систему, получаем таблицу приближенных значений искомой функции.
Более
точные формулы получаются, если заменить
![]() центрально-разностными отношениями:
центрально-разностными отношениями:
|
|
(1.17) |
а на концах отрезка положить:
|
|
(1.18) |
Используя эти формулы, приближенно заменим уравнения (1.12)–(1.13) системой уравнений:
|
|
(1.19) |
Приближенное решение обыкновенных дифференциальных уравнений методом прогонки
При большом n непосредственное решение системы (1.16) становится громоздким. Поэтому были разработаны различные методы решения систем такого вида, например, метод прогонки.
Рассмотрим систему (1.16). Метод прогонки решения системы заключается в следующем.
Запишем уравнения системы (1.14) в виде:
![]() ,
,
где
|
|
(1.23) |
Полученную систему приводим к виду:
|
|
(1.24) |
Числа
![]() последовательно вычисляются по формулам:
последовательно вычисляются по формулам:
при
![]()
|
|
(1.25) |
При
![]()
|
|
(1.26) |
Вычисления производятся в следующем порядке.
Прямой
ход. По
формулам (1.23) вычисляем значения
![]() .
Находим
.
Находим![]() по формулам (1.25). Затем вычисляем
по формулам (1.25). Затем вычисляем![]() по формулам (1.26) для
по формулам (1.26) для![]()
Обратный
ход. Из
уравнения (1.24) при
![]() и последнего уравнения системы (1.16)
получаем:
и последнего уравнения системы (1.16)
получаем:
![]()
Решив
эту систему относительно
![]() ,
будем иметь
,
будем иметь
|
|
(1.27) |
Используя
уже известные числа
![]() ,
находим
,
находим![]() .
Затем вычисляем значения
.
Затем вычисляем значения![]() ,
последовательно применяя рекуррентные
формулы (1.22):
,
последовательно применяя рекуррентные
формулы (1.22):
|
|
(1.28) |
Значение
![]() находим из предпоследнего уравнения
системы (1.16):
находим из предпоследнего уравнения
системы (1.16):
|
|
(1.29) |
Таким образом, все вычисления «прогоняются» два раза.
Вычисления
прямого хода заготавливают вспомогательные
числа
![]() в порядке возрастания индекса
в порядке возрастания индекса![]() .
При этом для вычисления значений
.
При этом для вычисления значений![]() используется краевое условие на левом
конце отрезка интегрирования. Затем на
первом шаге обратного хода происходит
согласование полученных чисел
используется краевое условие на левом
конце отрезка интегрирования. Затем на
первом шаге обратного хода происходит
согласование полученных чисел![]() с краевым условием на правом конце
отрезка интегрирования, после чего
последовательно получаются значения
искомой функции
с краевым условием на правом конце
отрезка интегрирования, после чего
последовательно получаются значения
искомой функции![]() в порядке убывания индекса
в порядке убывания индекса![]() .
.