14. Рекуррентные соотношения

Рек соотнош-я

Последовательность называют возвратной степени k, если для некоторого k и всех n выполняется:

A_(n+k) + pi*a_(n+k-1) + … + pk*an = 0 (*1*).

pi (i=1..k) = const

aj — элемент последовательности.

Такая возвратная последовательность характеризуется следующим многочленом (характеристическим):

P(x) = x^k + p1*x^(k-1) + … + pk.

Для решения (*1*) используем корни многочлена.

Сформулируем следующее утверждения (св-ва возвратной последовательности):

1) если лямбда является корнем характеристического многочлена, то последовательность лямбда^n удовлетворяет (*1*), -~ проверить подстановкой;

2) если лямбда1, лямбда2,…,лямбдаk — простые корни характеристического многочлена, то общее решение (*1*) представимо в виде:

an = c1*(лямбда1)^n + c2*(лямбда2)^n + … + ck*(лямбдаk)^n, где ci = const;

3) Рассмотрим случай, когда корни хар. мн-на — кратные:

лямбда1, лямбда2,…,лямбдаs — корни хар. мн-на соответствующей кратности r1,r2,…,rs.

Тогда общее решение (*1*) примет вид:

an = SUM(i=1..s)( (c_(i,1) + c_(i,2)*n + … + c_(i,r_i)*n^(r_i - 1) * (лямбдаi)^n).

Проверить, что выр-е an в условиях (2) и (3) является решением (*1*) -~ непосредственной подстановкой в (*1*).

--------

Задачи:

Найти общее решение рекуррентного соотношения:

1)a_(n+2) – 4*a(n+1) + 3*an = 0.

k=2

P(x) = x^2-4x+3.

Простое решение:

{x1 = 3

{x2 = 1

Общее:

an = c1*3^n + c2*1^n.

=> an = c1*3^n + c2.

2)

a_(n+3) + 10*a_(n+2) + 32*a_(n+1) + 32*an = 0.

k = 3

P(x) = x^3 + 10*x^2 + 32x + 32.

Простые корни: -4;-4;-2.

Общее решение:

=> an = c1*(-2)^n + (c2+c3*n)*(-4)^n.

3)

an = ? по рекуррентным соотношениям и начальным условиям

a_(n+2) – an = 0;

a0 = 0;

a1 = 2.

k = 2.

P(x) = x^2 + 1.

Простые корни: x1 = 1; x2 = -1.

an = c1*(-1)^n + c2*1^n = c1*(-1)^n + c2.

n = 0:

c1 + c2 = 0.

n = 1:

-c1 + c2 = 2.

{c1 + c2 = 0

{-c1 + c2 = 2

{c2 = 1

{c1 = -1

=>

an = (-1)^(n+1) + 1.

15. Булевы функции. Представление булевых функций полиномами Жегалкина.

В теории дискретных функциональных систем булевой функцией называют функцию типа , где—булево множество, а n — неотрицательное целое число, которое называют арностью или местностью функции. Элементы 1 (единица) и 0 (ноль) стандартно интерпретируют как истину и ложь, хотя в общем случае их смысл может быть любым. Элементы называютбулевыми векторами. В случае n = 0 булева функция превращается в булеву константу.

Основные сведения. Каждая булева функция арности n полностью определяется заданием своих значений на своей области определения, то есть на всех булевых векторах длины n. Число таких векторов равно 2ⁿ. Поскольку на каждом векторе функция может принимать значение либо 0, либо 1, количество всех n-арных булевых функций равно . Практически все булевы функции малых арностей (0, 1 и 2) сложились исторически и имеют конкретные имена. Если значение функции не зависит от одной из переменных(т.е. строго говоря для любых двух булевых векторов, отличающихся лишь в значении этой переменной, значение функции на них совпадает), то эта переменная называетсянесущественной.

Нульарные функции. При n = 0 количество булевых функций сводится к двум, первая из них тождественно равна 0, а вторая 1. Их называют булевыми константами.

• Унарные функции. При n = 1 число булевых функций равно .

• Бинарные функции. При n = 2 число булевых функций равно .

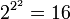Полные системы булевых функций

Суперпозиция и замкнутые классы функций. Результат вычисления булевой функции может быть использован в качестве одного из агрументов другой функции. Результат такой операции суперпозиции можно рассматривать как новую булеву функцию.

Замкнутые множества функций называют также замкнутыми классами. В качестве простейших примеров замкнутых классов булевых функций можно назвать множество {x}, состоящее из одной тождественной функции, или множество {0}, все функции из которого тождественно равны нулю вне зависимости от своих аргументов. Замкнуты также множество функций и множество всех унарных функций. А вотобъединение замкнутых классов может таковым уже не являться. Например, объединив классы {0} и , мы с помощью суперпозициисможем получить константу 1, которая в исходных классах отсутствовала.

Разумеется, множество P₂ всех возможных булевых функций тоже является замкнутым.

Тождественность и двойственность

Две булевы функции тождественны друг другу, если на любых одинаковых наборах аргументов они принимают равные значения. Тождественность функций f и g можно записать, например, так:

Полнота системы, критерий Поста

Система булевых функций называется полной, если можно построить их суперпозицию, тождественную любой другой заранее заданной функции. Говорят ещё, что замыкание данной системы совпадает с множеством P₂. Американский математик Эмиль Пост ввёл в рассмотрение следующие замкнутые классы булевых функций:

• Функции, сохраняющие константу T₀ и T₁;

• Самодвойственные функции S;

• Монотонные функции M;

• Линейные функции L.

Им было доказано, что любой замкнутый класс булевых функций, не совпадающий с P₂, целиком содержится в одном из этих пяти так называемых предполных классов, но при этом ни один из пяти не содержится целиком в объединении четырёх других. Таким образом критерий Поста для полноты системы сводится к выяснению, не содержится ли вся эта система целиком в одном из предполных классов. Если для каждого класса в системе найдётся функция, не входящая в него, то такая система будет полной, и с помощью входящих в неё функций можно будет получить любую другую булеву функцию.

Заметим, что существуют функции, не входящие ни в один из классов Поста. Любая такая функция сама по себе образует полную систему. В качестве примеров можно назвать штрих Шеффера или стрелку Пирса.

Представление булевых функций

Теорема Поста открывает путь к представлению булевых функций, синтаксическим способом, который в ряде случаев оказывается намного удобнее чем таблицами истинности. Отправной точкой здесь служит нахождение некоторой полной системы функций . Тогда каждая булева функция сможет быть представлена некоторымтермом в сигнатуре Σ, который в данном случае называют также формулой. Относительно выбраной системы функций полезно знать ответы на следующие вопросы:

• Как построить по данной функции представляющую её формулу?

• Как проверить, что две разные формулы эквивалентны, то есть задают одну и ту же функцию?

• В частности: существует ли способ приведения произвольной формулы к эквивалентной её канонической форме, такой что, две формулы эквивалентны тогда и только тогда, когда их канонические формы совпадают?

• Как по данной функции построить представляющую её формулу с теми или иными заданными свойствами (например наименьшего размера), и возможно ли это?

• Положительные ответы на эти и другие вопросы существенно увеличивают прикладное значение выбранной системы функций.

Простой конъюнкцией, или конъюнктом, называется конъюнкция некоторого конечного набора переменных, или их отрицаний, причём каждая переменная встречается не более одного раза. Дизъюнктивной нормальной формой или ДНФ называется дизъюнкция простых конъюнкций. Например — является ДНФ.

Совершенной дизъюнктивной нормальной формой, или СДНФ относительно некоторого заданного конечного набора переменных называется такая ДНФ, у которой в каждую конъюнкцию входят все переменные данного набора, причём в одном и том же порядке. Например: .

Легко убедиться, что каждой булевой функции соответствует некоторая ДНФ, и даже СДНФ. Для этого достаточно взять таблицу истинности этой функции и найти все булевы векторы, на которых её значение равно 1. Для каждого такого вектора строится конъюнкция, где. Если взять дизъюнкцию этих конъюнкций, то результатом очевидно будет СДНФ. Поскольку на всех булевых векторах её значения совпадают со значениями исходной функции, она будет СДНФ этой функции. Например, для импликации, результатом будет, что можно упростить до.

Конъюнктивная нормальная форма (КНФ) определяется двойственно к ДНФ. Простой дизъюнкцией или дизъюнктом называется дизъюнкция одной или нескольких переменных или их отрицаний, причём каждая переменная входит в неё не более одного раза. КНФ — это конъюнкция простых дизъюнкций.

Совершенной конъюнктивной нормальной формой (СКНФ), относительно некоторого заданного конечного набора переменных, называется такая КНФ, у которой в каждую дизъюнкцию входят все переменные данного набора, причём в одном и том же порядке. Поскольку (С)КНФ и (С)ДНФ взаимодвойственны, свойства (С)КНФ повторяют все свойства (С)ДНФ, грубо говоря, «с точностью до наоборот».

КНФ может быть преобразована к эквивалентной ей ДНФ, путём раскрытия скобок по правилу:

которое выражает дистрибутивность конъюнкции относительно дизъюнкции. После этого, необходимо в каждой конъюнкции удалить повторяющиеся переменные или их отрицания, а также выбросить из дизъюнкции все конъюнкции, в которых встречается переменная вместе со своим отрицанием. При этом, результатом не обязательно будет СДНФ, даже если исходная КНФ была СКНФ. Точно также, можно всегда перейти от ДНФ к КНФ. Для этого следует использовать правило

выражающее дистрибутивность дизъюнкции относительно конъюнкции. Результат нужно преобразовать способом, описанным выше, заменив слово «конъюнкция» на «дизъюнкция» и наоборот.

Полином Жегалкина это форма представления логической функции с помощью Функции Жегалкина (Исключающее ИЛИ). Для получения полинома Жегалкина следует выполнить следуюющие действия:

1. Получить ДНФ функции

2. Все ИЛИ заменить на Исключающее ИЛИ

3. Во всех термах заменить элементы с отрицанием на конструкцию: («элемент» «исключающее ИЛИ» 1)

4. Раскрыть скобки по правилам алгебры Жегалкина и привести попарно одинаковые термы