Примерный тематический план проведения лабораторных работ

В тематическом плане приведено примерное планирование часов, которые отводятся на каждую лабораторную работу.

В зависимости от используемого программного обеспечения число часов, необходимых для выполнения заданий, может быть уменьшено.

Тематический план проведения лабораторных работ

1.  Приближенное решение обыкновенных дифференциальных уравнений методом последовательных приближений – 4 часа.

2. Приближенное решение обыкновенных дифференциальных уравнений. Методы Эйлера, Эйлера Коши, Рунге-Кутта – 4 часа.

3. Приближенное решение обыкновенных дифференциальных уравнений. Метод Адамса. Методы прогноза-коррекции – 4 часа.

4. Приближенное решение обыкновенных дифференциальных уравнений методом конечных разностей – 2 часа

5. Приближенное решение обыкновенных дифференциальных уравнений методом прогонки – 4 часа.

6. Метод сеток для задачи Дирихле – 4 часа.

7. Итерационный метод решения системы конечно-разностных уравнений (процесс усреднения Либмана) – 4 часа.

8. Решение уравнения Фредгольма второго рода методом конечных сумм – 4 часа.

9. Метод обработки статистических данных – 4 часа.

Глава 1. Приближенные методы решения обыкновенных дифферен-циальных уравнений

1.1. Справочные материалы по приближенным методам решения обыкновенных дифференциальных равнений

1.1.1. Постановка задачи Коши

Рассмотрим обыкновенное дифференциальное уравнение первого порядка:

. (1.1)

Основная задача, связанная с этим уравнением – задача Коши состоит в следующем: найти решение уравнения (1.1) в виде функции удовлетворяющей начальному условию:

. (1.2)

Геометрически это означает, что требуется найти интегральную кривую проходящую через заданную точкупри выполнения равенства (1.1). Существование и единственность решения уравнения (1.1) обеспечивается следующей теоремой.

Теорема Пикара: Если функцияf определена и непрерывна в некоторой областиG, определённой неравенствами:

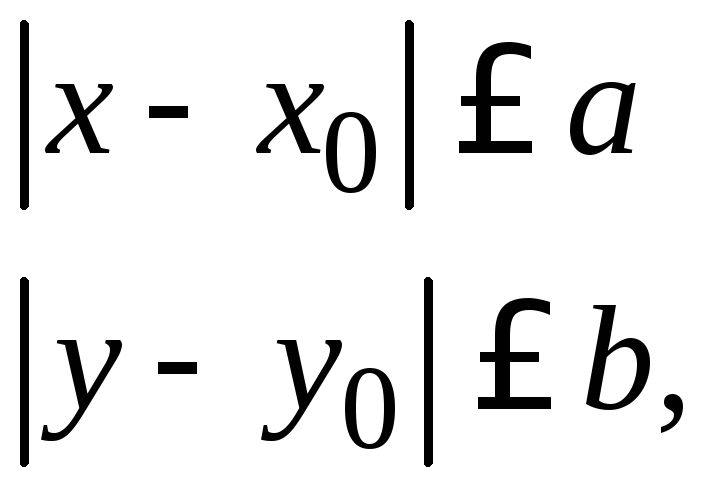(1.3)

и удовлетворяет в этой области условию Липшица по у:, то на некотором отрезке, гдеh– положительное число, существует, и притом только одно, решениеуравнения (1.1), удовлетворяющее начальному условию.

Здесь М– постоянная (константа Липшица), зависящая в общем случае ота иb.

Если f(x, y)имеет ограниченную вGпроизводную, то приможно принять.

В классическом анализе разработаны методы нахождения решений дифференциальных уравнений через элементарные (или специальные) функции. На практике эти методы очень часто оказываются либо совсем беспомощными, либо их использование требует трудных вычислений и времени.

Для решения практических задач созданы методы приближённого решения дифференциальных уравнений.

Пусть требуется на отрезке [х₀, х₀₀+Н] найти решение уравнения (1.1) при начальном условии (1.2).

Разобьём отрезок на п равных частей точками: ,где .

Численное решение дифференциального уравнения (1.1) заключается в том, что значение искомой функции вычисляется в каждой точке. При этом, как правило, для вычисления значенияиспользуется уже вычисленное значение.

Для решения задачи Коши для обыкновенных дифференциальных уравнений существуют различные методы:

1. Аналитические методы, применение которых дает решение дифференциального уравнения в виде аналитического выражения.

2. Графические методы, дающие приближенное решение в виде графиков.

3. Численные методы (табличные), при использовании которых искомая функция получается в виде таблицы.

Ниже рассматриваются относящиеся к указанным группам некоторые методы решения обыкновенных дифференциальных уравнений первого порядка вида (1.1).