5.1 Минимизация двоичных функции

Пусть двоичная функция f представлена в виде ДНФ:

. (5.1)

Определение 5.1. Сложностью представления (5.1) булевой функции f называется число операций «» и «» в записи (5.1).

Замечание 5.2. Операции «отрицания» в определении 5.1 не учитываются.

Определение 5.3. Задача минимизации для функции f заключается в нахождении заданий функции f в виде ДНФ, у которых сложности минимальны. Такие ДНФ называются минимальными (МДНФ).

Определение 5.4. Импликантами двоичной функции f называются элементарные конъюнкции, входящие во всевозможные ДНФ функции f. Импликанта функцииf называется простой, если все элементарные конъюнкции, полученные из неё удалением некоторых переменных, не являются импликантами функции f.

Утверждение 5.5. Пусть . Следующие утверждения эквивалентны:

1.является импликантой функцииf;

2.;

3..

Доказательство. Покажем эквивалентность первых двух утверждений. Если — импликанта и— та ДНФ, в которую входит, например,, то

.

Обратно, если — некоторая ДНФ, то в силу тождестваконъюнкцию можнодописать в качестве (k + 1)-й импликанты в эту ДНФ не нарушая равносильности. Эквивалентность утверждений 2 и 3 следует из тождеств:

, .

Утверждение доказано.

Утверждение 5.6. В минимальной ДНФ функции f () все импликанты являются простыми.

Доказательство. Пусть — минимальная ДНФ функцииf. Предположим, что импликанта непростая. Тогда её можно представить в виде произведениядвух элементарных конъюнкций от разных переменных, одна из которых, например, также является импликантой функцииf. Согласно утверждению 5.5: , или иначе

.

Таким образом, получено противоречие с минимальностью исходной ДНФ. Утверждение доказано.

Из этого утверждения вытекает, что задачу минимизации в классе ДНФ можно решать в два этапа.

1-й этап. Находят все простые импликанты функции f. Дизъюнкция всех простых импликант функции f называется сокращённой ДНФ этой функции.

Замечание 5.7. Сокращённая ДНФ функции f действительно является ДНФ для f, поскольку, повторяя доказательство утверждения 5.6 можно в произвольной ДНФ функции f заменить все импликанты на простые.

2-й этап. Находят все такие ДНФ функции f, состоящие из простых импликант, из которых нельзя удалить ни одной импликанты. Такие ДНФ называются тупиковыми или несократимыми. Подсчитав сложности тупиковых ДНФ, можно выбрать из них ТДНФ с минимальной сложностью, которая и есть МДНФ.

5.2. Геометрическая интерпретация минимизации днф

Зададим двоичную функцию на n-мерном двоичном кубе. Как было отмечено ранее, при таком задании элементарным конъюнкциям ранга k соответствуют такие множества вершин, графы связности которых имеют вид (k – n)-мерных кубов. Поскольку дизъюнкции элементарных конъюнкций соответствует объединение множеств вершин таких подкубов, то каждой ДНФ функции f соответствует некоторое покрытие множества M_f единичных вершин функции f (области истинности) подмножествами, имеющими в качестве графов связности подкубы. Простым импликантам функции f будут соответствовать подкубы максимальных размерностей, покрывающие вершины из M_f.

Соответственно, первая задача (1-й этап) решается перечислением всех максимальных подкубов, содержащихся в графе связности множества M_f. Вторая задача (2-й этап) заключается в нахождении минимальных (по числу подкубов) покрытий множества M_f максимальными подкубами.

Рассмотрим пример. Пусть двоичная функция f (x₁, x₂, x₃, x₄) имеет геометрическое задание, изображённое на рис.5.1.

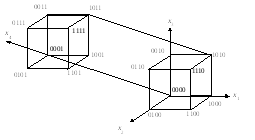
Рис.5.1

Граф связности такой функции имеет вид рис.5.2.

1110

0111

0011

1110

1000

1010

1100

1110

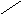
Рис.5.2

Выпишем сокращённую ДНФ, записывая простые импликанты в том же порядке, в каком они изображены в графе связности:

.

Легко видеть, что тупиковыми будут две ДНФ:

, ,

соответствующие покрытиям (рис.5.3).

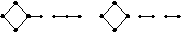
Рис.5.3

Минимальной будет только вторая тупиковая ДНФ.

Л е к ц и я 6