
- •Ф.К. Алиев, и.А. Юров
- •Введение
- •Основные способы задания двоичных функций
- •1.1. Табличный способ задания
- •1.2. Геометрический способ задания
- •1.3. Задание двоичных функций формулами
- •Основные способы задания двоичных функций (продолжение)
- •2.1. Нормальные формы двоичных функций
- •2.2. Многочлен Жегалкина и действительный многочлен двоичной функции
- •2.3. Теорема о разложении в ряд Фурье
- •Полнота и замкнутость. Критерий полноты системы. Функционально полные системы. Замкнутые классы булевых функций
- •3.1. Полнота и замкнутость. Функционально полные системы
- •3.2. Замкнутые классы булевых функций
- •3.3. Критерий полноты системы булевых функций
- •4.1. Псевдобулевы функции
- •4.2. Функции k-значной логики
- •5.1 Минимизация двоичных функции
- •5.2. Геометрическая интерпретация минимизации днф
- •6.1. Метод Квайна — Мак-Класки нахождения сокращённой днф двоичной функции
- •6.2. Метод нахождения тупиковых днф
- •6.3. Метод Петрика нахождения тупиковых днф
- •Алгебраические системы
- •7.1. Алгебраические системы. Булевы алгебры
- •7.2. Изоморфизм алгебраических систем
- •Алгебры высказываний. Предикаты и операции над ними
- •8.1. Основные логические операции и их свойства
- •8.2. Предикаты и операции над ними
- •Исчисление предикатов
- •9.1. Общее понятие о логическом исчислении
- •9.2. Формулы алгебры предикатов
- •9.3. Равносильность формул. Основные отношения равносильности
- •9.4. Использование равносильностей для упрощения формул
- •9.5. Построение исчисления предикатов
- •9.6. Выводимость и доказуемость формул
- •9.7. Семантика исчисления предикатов
- •Понятие о теории моделей
- •Элементы теории алгоритмов
- •11.1. Основные требования к алгоритмам
- •11.2. Машина Тьюринга и функции, вычислимые по Тьюрингу
- •11.3. Машины произвольного доступа и вычислимые функции
- •Частично рекурсивные функции и их вычислимость
- •Вычислимость суперпозиции
- •Вычислимость рекурсии
- •Вычислимость минимизации
- •Нумерация наборов чисел и слов
- •Нормальные алгоритмы
- •Нумерация алгоритмов
- •1. Нумерация машин Тьюринга
- •2. Нумерация мпд-программ
- •Универсальные функции
- •Алгоритмически неразрешимые проблемы
- •16.1. Алгоритмически неразрешимые проблемы
- •16.2. Примечательные алгоритмически неразрешимые проблемы
- •Характеристики сложности вычислений
- •Характеристика сложности вычислительных задач
- •18.1. Классы сложности p и np и их взаимосвязь
- •18.3. Основные np-полные задачи. Сильная np-полнота
- •Список Литературы
6.3. Метод Петрика нахождения тупиковых днф
Рассмотрим табл.6.2, строки которой соответствуют простым импликантам функции f, а столбцы — конъюнкциям совершенной ДНФ (СДНФ). В каждую клетку записываем единицу, если соответствующая простая импликанта поглощает элементарную конъюнкцию и нуль — в противном случае. Такая таблица называется «импликантной таблицей».
Согласно определению, каждая тупиковая ДНФ определяется таким набором строк, что в таблице, образованной этими строками в каждом столбце имеется одна единица, причём из этого набора нельзя удалить ни одной строки так, чтобы при этом ни один столбец не стал нулевым.
Таблица 6.2
|
СДНФ Сокр. ДНФ |
1000 |
1100 |
1010 |
0101 |
0011 |
1110 |
1011 |
0111 | |
|
P1 |
1__0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
|
P2 |
101_ |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
|
P3 |
_001 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
|
P4 |
0_11 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
|
P5 |
01_1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
Пусть в общем случае в таблице имеется N столбцов и m строк. Поставим в соответствие простым импликантам сокращённой ДНФ переменные P1 … Pm. Фиксируем некоторую дизъюнкцию простых импликант. Будем считать, что Pi = 1, если i-я простая импликанта входит в эту дизъюнкцию и Pi = 0, в противном случае. Запишем в виде формалы условие того, что рассматриваемая дизъюнкция является ДНФ функции. Для этого необходимо, чтобы в каждом столбце таблицы была хотя бы одна единица, т.е.
![]() ,
,
где
![]() —
элемент матрицы (таблицы), стоящий вi-й
строке и j-м
столбце,
—
элемент матрицы (таблицы), стоящий вi-й
строке и j-м
столбце,
![]() .
.
Эту формулу можно трактовать как КНФ некоторой двоичной функции от переменных P1 … Pm, которая принимает значение 1 только на тех наборах переменных, которые соответствуют некоторым ДНФ исходной функции, и значение 0 — на наборах, которые соответствуют наборам импликант, не являющихся ДНФ исходной функции.
Заметим,
что функция
![]() монотонна, так как формула 6.2.3 не содержит
переменных с отрицаниями. Поэтому
согласно утверждению 6.3 для нахождения
её сокращённой ДНФ достаточно раскрыть
скобки в формуле 6.2.3, а затем произвести
все поглощения. Наконец, остаётся
заметить, что в силу указанного выше
свойства этой функции, её простые
импликанты и только они будут давать
тупиковые ДНФ исходной функцииf.
монотонна, так как формула 6.2.3 не содержит
переменных с отрицаниями. Поэтому
согласно утверждению 6.3 для нахождения
её сокращённой ДНФ достаточно раскрыть
скобки в формуле 6.2.3, а затем произвести
все поглощения. Наконец, остаётся
заметить, что в силу указанного выше
свойства этой функции, её простые
импликанты и только они будут давать
тупиковые ДНФ исходной функцииf.
Для
табл. 6.2 функция
![]() равна:
равна:
![]()
![]()
![]()
![]() .
.
Отсюда P1P3P5 даёт для f тупиковую форму:
![]() ,
,
а P1P2P4P5 даёт:
![]() .
.
Л е к ц и я 7
Алгебраические системы
7.1. Алгебраические системы. Булевы алгебры
Определение 7.1. Множество M с заданными на нём операциями и отношениями называется алгебраической системой. При этом M называется основным множеством системы, а множество символов, используемых для обозначения определённых на M операций и отношений называется сигнатурой алгебраической системы.
Алгебраическую
систему с основным множеством M
и сигнатурой
![]() ,
состоящий из символов операцийfi
арностей ni
и отношений Rj
арностей mj,
обозначают в виде M(
,
состоящий из символов операцийfi
арностей ni
и отношений Rj
арностей mj,
обозначают в виде M(![]() ),
или подробнееM(
),
или подробнееM(![]() ).
При этом набор натуральных чисел
<n1, …, nk;
m1, …, ml>
называется типом алгебраической системы
M(
).
При этом набор натуральных чисел
<n1, …, nk;
m1, …, ml>
называется типом алгебраической системы
M(![]() ).
Если на алгебраической системе определены
только операции, то она называетсяалгеброй.
Если на алгебраической системе только
отношения, то она называется моделью.
).
Если на алгебраической системе определены
только операции, то она называетсяалгеброй.
Если на алгебраической системе только
отношения, то она называется моделью.
Пример 7.2. N(+, *; =, <) — алгебраическая система.
Пример 7.3. N(+, *) — алгебра.
Пример 7.4. N(+, <) — модель.
Пример 7.5. Алгебрами являются полугруппы, группы, кольца, поля и т.д.
В математической логике особую роль играют так называемые булевы алгебры.
Определение
7.6. Булевой
алгеброй называется множество B
с двумя бинарными операциями «![]() »,
«
»,
«![]() »,
и одной унарной операцией «»
и двумя нуль-арными операциями (т.е.
выделенными элементами) 0, 1, удовлетворяющими
условиям (при любых
»,
и одной унарной операцией «»
и двумя нуль-арными операциями (т.е.
выделенными элементами) 0, 1, удовлетворяющими
условиям (при любых
![]() ):
):
1. ![]() ,
,
2. ![]() ,
,
3. ![]() ,
,
4. ![]() ,
,
5. ![]() ,
,
6. ![]() ,
,
7. ![]() ,
,
8. ![]() ,
,
9. ![]() ,
,
10. ![]() ,
,
11. ![]() ,
,
12. ![]() .
.
Несложно показать, что из условий 1-12 следуют равенства:
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() .
.
Например,
выведем из условий 1-12 равенство
![]() :
:
![]() .
.
Элементы 0 и 1 булевой алгебры B называют её нулём и единицей. Иногда их обозначают в виде 0B и 1B.
Пример
7.7. Пусть
2M —
обозначение множества всех подмножеств
множества M,
![]() —
бинарная операция пересечения множеств,
—
бинарная операция пересечения множеств,![]() —
бинарная операция объединения множеств.
ДляA
—
бинарная операция объединения множеств.
ДляA ![]() M
обозначим A = M\A,
A —
дополнение множества A.
«» —
унарная операция,
M
обозначим A = M\A,
A —
дополнение множества A.
«» —
унарная операция,
![]() иM
– нуль-арные операции, играющие роль 0
и 1. Тогда 2M(
иM
– нуль-арные операции, играющие роль 0
и 1. Тогда 2M(![]() ,
, ![]() ,
, ![]() , M) —
булева алгебра.
, M) —
булева алгебра.
Пример
7.8. Пусть M —
множество всех положительных делителей
числа m,
равного произведению некоторых различных
простых чисел. Определим операции «![]() »,
«
»,
«![]() »
и «»
следующим образом: для любых
»
и «»
следующим образом: для любых
![]() M
положим
M
положим
![]() ,
,![]() ,
,![]() .
Число 1M
играет роль нуль-арной операции 0. Число
m
M
играет роль нуль-арной операции 1. Тогда
M(
.
Число 1M
играет роль нуль-арной операции 0. Число
m
M
играет роль нуль-арной операции 1. Тогда
M(![]() ,
,![]() ,, 1, m) —
булева алгебра.
,, 1, m) —
булева алгебра.
Определение
7.9. Пусть
![]() —
бинарное отношение на наM.
Бинарное отношение
—
бинарное отношение на наM.
Бинарное отношение
![]() на множествеM
называется отношением
частичного порядка
(или просто отношением порядка), если
оно рефлексивно, транзитивно,
антисимметрично. Отношение частичного
порядка
на М
называется отношением линейного порядка,
если для любых x,
x M
либо x
x,
либо x
x.
Отношение порядка обозначается через
«
на множествеM
называется отношением
частичного порядка
(или просто отношением порядка), если
оно рефлексивно, транзитивно,
антисимметрично. Отношение частичного
порядка
на М
называется отношением линейного порядка,
если для любых x,
x M
либо x
x,
либо x
x.
Отношение порядка обозначается через
«![]() ».
Если
».
Если![]() и
и![]() ,
то пишут
,
то пишут![]() .
.
Множество
M
с заданным на нём отношением частичного
или линейного порядка «![]() »
называется, соответственно, частично
или линейно упорядоченным множеством.
»
называется, соответственно, частично
или линейно упорядоченным множеством.
В
некоторых случаях при изучении частично
упорядоченных множеств используются
их геометрические изображения —
диаграммы. При построении диаграмм
частично упорядоченного множества M(![]() )
различные элементы изM
отождествляются с различными точками
плоскости так, что:
)
различные элементы изM
отождествляются с различными точками
плоскости так, что:
точка
![]() лежит левее (или ниже) точки
лежит левее (или ниже) точки![]() ,
если
,
если![]() ;
;
точка
![]() соединяется отрезком с отличной от неё
точкой
соединяется отрезком с отличной от неё
точкой![]() ,
если
,
если![]() и не существует точки
и не существует точки![]() ,
отличной отa,
b,
удовлетворяющей условию
,
отличной отa,
b,
удовлетворяющей условию
![]() (в этом случае говорят, чтоb
непосредственно следует за a
или a
непосредственно предшествует b).
(в этом случае говорят, чтоb
непосредственно следует за a
или a
непосредственно предшествует b).
Пример 7.10. M = 2{1, 2, 3}.
Положим
для любых A, B ![]() M,
M,
![]() .
Тогда диаграмма дляM(
.
Тогда диаграмма дляM(![]() )
представляется рис.7.1.
)
представляется рис.7.1.
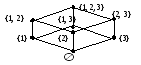
Рис.7.1
Пример
7.11. M = {![]() }.
}.
Положим
a ![]() b
«натуральное число a»
b
«натуральное число a»
![]() «натурального числаb».
Тогда диаграмма для M(
«натурального числаb».
Тогда диаграмма для M(![]() )
имеет вид, показанный на рис.7.2.
)
имеет вид, показанный на рис.7.2.
n n–1 3 2 1




Рис.7.2
Пример 7.12. M = {1, 2, 3, 4, 5, 6}.
Положим
a ![]() b
b ![]() a
| b
для любых a,
b
a
| b
для любых a,
b
![]() M.
Тогда диаграмма для M(
M.
Тогда диаграмма для M(![]() )
имеет вид (рис.7.3).
)
имеет вид (рис.7.3).

Рис.7.3
Интересно отметить связь булевых алгебр с частично упорядоченными множествами.
Пусть
B —
произвольная булева алгебра. Для
произвольных элементов a,
b ![]() B
положим a
B
положим a ![]() b
b ![]() a
a ![]() b = b.
b = b.
Из
условий 6.4.2 следует, соответственно,
что так определённое отношение «![]() »
наB
рефлексивно, антисимметрично и
транзитивно. В итоге имеем частично
упорядоченное множество B(
»
наB
рефлексивно, антисимметрично и
транзитивно. В итоге имеем частично
упорядоченное множество B(![]() ).
Диаграмма дляB(
).
Диаграмма дляB(![]() )
называется диаграммойбулевой
алгебры B.
Таким образом на рис.7.1 изображена
диаграмма булевой алгебры всех надмножеств
множества {1, 2, 3}.
)
называется диаграммойбулевой
алгебры B.
Таким образом на рис.7.1 изображена
диаграмма булевой алгебры всех надмножеств
множества {1, 2, 3}.
