
- •Ф.К. Алиев, и.А. Юров
- •Введение
- •Основные способы задания двоичных функций
- •1.1. Табличный способ задания
- •1.2. Геометрический способ задания
- •1.3. Задание двоичных функций формулами
- •Основные способы задания двоичных функций (продолжение)
- •2.1. Нормальные формы двоичных функций
- •2.2. Многочлен Жегалкина и действительный многочлен двоичной функции
- •2.3. Теорема о разложении в ряд Фурье
- •Полнота и замкнутость. Критерий полноты системы. Функционально полные системы. Замкнутые классы булевых функций
- •3.1. Полнота и замкнутость. Функционально полные системы
- •3.2. Замкнутые классы булевых функций
- •3.3. Критерий полноты системы булевых функций
- •4.1. Псевдобулевы функции
- •4.2. Функции k-значной логики
- •5.1 Минимизация двоичных функции
- •5.2. Геометрическая интерпретация минимизации днф
- •6.1. Метод Квайна — Мак-Класки нахождения сокращённой днф двоичной функции
- •6.2. Метод нахождения тупиковых днф
- •6.3. Метод Петрика нахождения тупиковых днф
- •Алгебраические системы
- •7.1. Алгебраические системы. Булевы алгебры
- •7.2. Изоморфизм алгебраических систем
- •Алгебры высказываний. Предикаты и операции над ними
- •8.1. Основные логические операции и их свойства
- •8.2. Предикаты и операции над ними
- •Исчисление предикатов
- •9.1. Общее понятие о логическом исчислении
- •9.2. Формулы алгебры предикатов
- •9.3. Равносильность формул. Основные отношения равносильности
- •9.4. Использование равносильностей для упрощения формул
- •9.5. Построение исчисления предикатов
- •9.6. Выводимость и доказуемость формул
- •9.7. Семантика исчисления предикатов
- •Понятие о теории моделей
- •Элементы теории алгоритмов
- •11.1. Основные требования к алгоритмам
- •11.2. Машина Тьюринга и функции, вычислимые по Тьюрингу
- •11.3. Машины произвольного доступа и вычислимые функции
- •Частично рекурсивные функции и их вычислимость
- •Вычислимость суперпозиции
- •Вычислимость рекурсии
- •Вычислимость минимизации
- •Нумерация наборов чисел и слов
- •Нормальные алгоритмы
- •Нумерация алгоритмов
- •1. Нумерация машин Тьюринга
- •2. Нумерация мпд-программ
- •Универсальные функции
- •Алгоритмически неразрешимые проблемы
- •16.1. Алгоритмически неразрешимые проблемы
- •16.2. Примечательные алгоритмически неразрешимые проблемы
- •Характеристики сложности вычислений
- •Характеристика сложности вычислительных задач
- •18.1. Классы сложности p и np и их взаимосвязь
- •18.3. Основные np-полные задачи. Сильная np-полнота
- •Список Литературы
Нормальные алгоритмы
В данной лекции дается представление об одном подходе к уточнению понятия алгоритма, предложенном А.А. Марковым и называемом нормальные алгоритмы (в авторской транскрипции — алгорифмы). Данный подход связывает неформальное понятие эффективности с переработкой слов в некотором конечном алфавите в соответствии с определенными правилами. В качестве элементарного преобразования используется подстановка одного слова вместо другого. Множество таких подстановок определяет схему алгоритма. Правила, определяющие порядок применения подстановок, а также правила останова являются общими для всех нормальных алгоритмов. Дадим формальные определения. Пусть А = {a1, …, an} — алфавит. Если P, Q — слова в алфавите А (возможно, пустые), то выражения P Q P Q называются формулами подстановки в алфавите А (предполагается, что знаки , не входят в алфавит А). При этом формула P Q называется простой, а формула P Q — заключительной. Обозначим P ()Q — любую из этих формул. Произвольная конечная последовательность таких формул называется схемой SN нормального алгоритма N. Значит схема нормального алгоритма имеет вид:
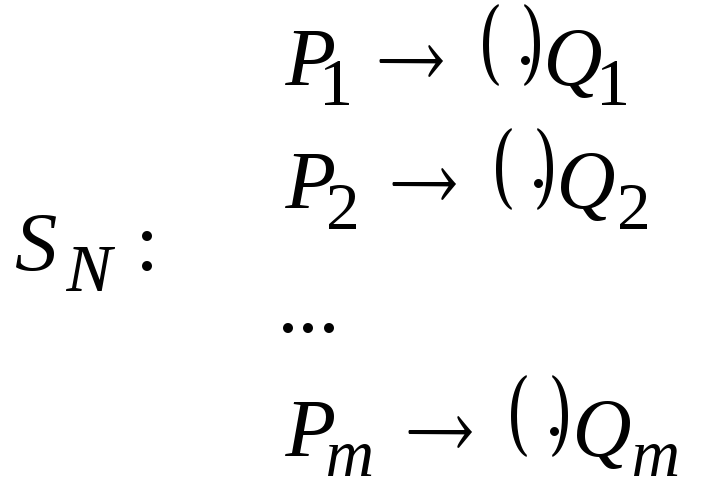
Схема SN определяет следующий алгоритм N, перерабатывающий слова в алфавите А (т.е. вычисляющий словарную функцию на словах в алфавите А). Говорим, что слово Р входит в слово W, если существуют слова V1 и V2 (возможно, пустые) такие, что W = = V1 P V2. Если слово V1 имеет наименьшую длину из всех слов такого вида, то говорят о первом вхождении Р в слово W.
Пусть дано произвольное слово К в алфавите А. Возможны следующие случаи:
1) ни одно из слов P1, …, Pm не входит в слово К. В этом случае говорим, что схема SN не применима к К и пишем SN : --|;
2) среди слов P1, …, Pm существует Pi, входящее в К.
Пусть
t —
минимальное число такое, что Pt
входит в К,
и пусть К = V1
Pt
V2,
где V1
имеет минимальную длину (т.е. берется
первое вхождение Pt
в К).
Тогда определим слово W = V1
Qt
V2.
В этом случае говорим, что схема SN
применима к К
и пишем SN :
К ![]() W
или SN :
К
W
или SN :
К ![]() W
в зависимости
от того, применялась простая формула
или заключительная соответственно.
W
в зависимости
от того, применялась простая формула
или заключительная соответственно.
Теперь
пишем SN
: К |![]() W,
если существует конечная последовательность
слов W0,
W1, … Wk
в алфавите А
такая , что К = W0,
W = Wk
и выполнено
W,
если существует конечная последовательность
слов W0,
W1, … Wk
в алфавите А
такая , что К = W0,
W = Wk
и выполнено
SN : W0 ![]() 1,
SN : W1
1,
SN : W1 ![]() W2,
…, SN : Wk – 1
W2,
…, SN : Wk – 1![]() Wk,
Wk,
либо
SN : Wk – 1 ![]() Wk.
Wk.
В
первом случае пишем также SN :
К |![]() W.
Говорим, что нормальный алгоритм N
со схемой SN
вычисляет словарную функцию Fs : A* A*,
где А* —
множество слов в алфавите А,
если для любых слов P, Q A*
имеем:
W.
Говорим, что нормальный алгоритм N
со схемой SN
вычисляет словарную функцию Fs : A* A*,
где А* —
множество слов в алфавите А,
если для любых слов P, Q A*
имеем:
Fs(P) = Q
Работа
нормального алгоритма может быть описана
так. Если дано слово Р,
то находим в схеме алгоритма SN
первую формулу Pt ()Qt
такую, что Pt
входит в Р,
и производим замену первого вхождения
Pt
словом Qt.
Пусть W1 —
результат этой подстановки. Если
применяемая формула Pt ()Qt —
заключительная, то работа алгоритма
заканчивается, и слово W1
есть результат работы алгоритма. Если
применяемая формула Pt Qt —
простая, то к слову W1
применяем описанную процедуру. Если на
некотором шаге получено слово Wi,
к которому не применима схема алгоритма
SN
(т.е. ни одно из не входит в Pj,
![]() ),
то работа алгоритма заканчивается, и
Wi
есть результат работы алгоритма. Если
описанный процесс не заканчивается,
то, по определению, алгоритм не применим
к слову Р.
),
то работа алгоритма заканчивается, и
Wi
есть результат работы алгоритма. Если
описанный процесс не заканчивается,
то, по определению, алгоритм не применим
к слову Р.
Словарная функция f в алфавите А (т.е. типа f : A* A*) называется вычислимой по Маркову, если существует схема нормального алгоритма SN в алфавите В А, вычисляющая f, т.е. Fs = f. Класс функций, вычислимых по Маркову, обозначим М.
Рассмотрим несколько примеров.
1) А = {a1, a2}.
Схема SN
:
![]() .
Данный алгоритм оставляет пустое слово
^ без изменения и всякое словоР
в алфавите А
переводит в слово Q,
полученное из Р
путем вычеркивания первого вхождения
буквы а1.
Алгоритм N
не применим к словам, не содержащим
вхождений буквы а1.
.
Данный алгоритм оставляет пустое слово
^ без изменения и всякое словоР
в алфавите А
переводит в слово Q,
полученное из Р
путем вычеркивания первого вхождения
буквы а1.
Алгоритм N
не применим к словам, не содержащим
вхождений буквы а1.
2) А = {a1, …, an}.
Схема
SN
:
![]() .
.
Данный алгоритм переводит всякое слово Р в алфавите А в пустое слово.
3) А = {1}.
Схема SN
:
![]() .
Данный алгоритм переводит всякое словоР =
.
Данный алгоритм переводит всякое словоР = ![]() в словоQ =
в словоQ = ![]() .
Если представить натуральное числоn
словом 1n + 1,
то данный алгоритм вычисляет функцию
f(n) = n + 1.
.
Если представить натуральное числоn
словом 1n + 1,
то данный алгоритм вычисляет функцию
f(n) = n + 1.
4) A = {a1, …, an}.
Схема
SN
:
![]() .
Данный
алгоритм вычисляет функцию Fs(P) = P,
для любого слова Р.
Если же взять схему SN
:
.
Данный
алгоритм вычисляет функцию Fs(P) = P,
для любого слова Р.
Если же взять схему SN
:
![]() ,
то данный алгоритм вычисляет нигде не
определенную функцию.
,
то данный алгоритм вычисляет нигде не
определенную функцию.
5) A = {a1, …, an}.
Если
![]() ,
то обращением слова Р
назовем слово
,
то обращением слова Р
назовем слово
![]() .
.
Рассмотрим алфавит В = А {, } и соответственно схему SN (, — новые буквы):
1.
2. a a, для любых a A
3.
4. ^
5. ab b a, для любых a, b A
6. ^ .
Покажем, что данный алгоритм N осуществляет обращение слов в алфавите А.
Пусть
![]() —
слово в алфавите А.
Тогда
—
слово в алфавите А.
Тогда
![]()
![]()
![]()
![]()
![]()
![]() .
.
Теперь, повторяя этот процесс, получим:
![]()
![]()
![]()
![]() .
.
Для нормальных алгоритмов разработана техника программирования, позволяющая осуществлять операции композиции алгоритмов, реализовывать операторы «если Ф, то выполнить F1, иначе F2», «пока Ф, выполнять F1, иначе F2». Следовательно, класс функций М достаточно широк. Много конкретных нормальных алгоритмов и соответствующая техника программирования представлены в книге «Теория алгорифмов»1. В связи с этим Марковым А.А. был выдвинут принцип нормализации, который заключается в том, что все алгоритмы исчерпываются нормальными алгоритмами или, что то же самое — всякий алгоритм нормализуем. Принятие данного принципа позволяет истолковывать утверждения о несуществовании нормальных алгоритмов для решения конкретных задач как утверждения о несуществовании алгоритмов вообще. Данный принцип эквивалентен тезисам Черча и Тьюринга, поскольку справедлива следующая теорема.
Теорема 14.1. Класс функций М, вычислимых по Маркову, совпадает с классом функций Т, вычислимых по Тьюрингу, и, следовательно, с классом частично рекурсивных функций Ч и с классом МПД, вычислимых функций Е.
Доказательство совпадения классов М и Ч проводится по той же схеме, что и приведенное выше доказательство совпадения классов Т и Ч2.
Л е к ц и я 15
