Введение

Данное учебное пособие является основой для преподавания курса «Математическая логика и теория алгоритмов». Этот курс преподается студентам третьего курса факультета «Информационная безопасность» МИФИ в рамках специальности «Комплексное обеспечение информационной безопасности автоматизированных систем» (шифр 075500).

В этом пособии отражены, по мнению авторов, теоретические результаты, лежащие в основе создания устройств криптографической защиты информации и оценки их стойкости. Так, например, один из подходов к анализу и обоснованию стойкости алгоритмов криптографической информации состоит в оценке вычислительной сложности соответствующих преобразований. Кроме того, большое число криптографических алгоритмов строятся на основе преобразований, которые реализованы с помощью булевых функций. Естественным образом возникает необходимость наличия у специалистов в области информационной безопасности навыков использования аппарата булевых функций и теории сложности вычисления для анализа криптографических преобразований. Теоретические основы для возможности реализации этих навыков приведены в данном учебном пособии.

Излагаемый материал представлен в виде 18 лекций. Объем лекций различен. Это, прежде всего, связано с тем, что определенные разделы курса предназначены для самостоятельного изучения. Так, например, весьма обширно представлены результаты, связанные с реализацией вычислительных процедур на таких моделях вычислительных устройств, как машины Тьюринга и МПД-машины. При этом изложение этих результатов, в целом, носит описательный характер и в полной мере доступен для успешной самостоятельной работы студентов. В учебном пособии приведено большое количество результатов, связанных с изучением конкретных вычислительных задач, что также может быть изучено самостоятельно.

Л е к ц и я 1

Основные способы задания двоичных функций

1.1. Табличный способ задания

Определение 1.1. Двоичной функцией от n (n  1) переменных называется функция , аргументы и значения которой выбираются из множеств, т.е.

f: ,

где

, .

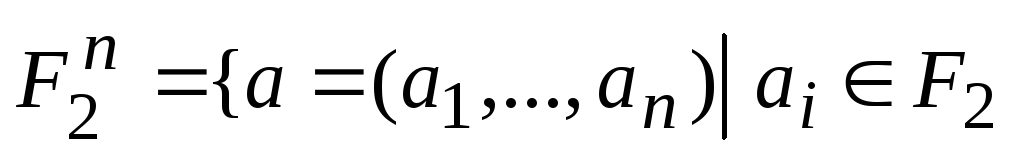Замечание 1.2. Двоичные функции от n переменных также называют булевыми (булевскими) функциями от n переменных или n-местными булевыми функциями.

На множестве определим так называемый лексикографический порядок, т.е. для любого двоичного набораопределим его номер

.

Тогда двоичная функция однозначно может быть задана табл.1.1 (называемой таблицей истинности).

Таблица 1.1

Номер набора	x1 … xn-1 xn	f(x1, ..., xn)
0	0 ... 0 0	f(0, ..., 0,0)
1	0 ... 0 1	f(0, ..., 0,1)
. . .	. . .	. . .
2^n – 2	1 ... 1 0	f(1, ..., 1,0)
2^n – 1	1 ... 1 1	f(1, ..., 1,1)

При указанной договоренности о расположении наборов из функция однозначно определяется набором — столбцом значений. Отсюда непосредственно вытекает справедливость следующего утверждения.

Утверждение 1.3. Число двоичных функций от n переменных равно .

Перечислим все двоичные функции от одной и двух переменных. Имеется четыре функции от одной переменной (табл.1.2).

Таблица 1.2

x1 \ f	f0	f1	f2	f3
0	0	0	1	1
1	0	1	0	1
Условное обозначение	0			1

Функции ине зависят от значения переменнойи называютсяконстантными (,). Функцияназываетсятождественной функцией, а функция называетсяотрицанием.

Функций от двух переменных — шестнадцать (табл.1.3).

Таблица 1.3

,\f	f0	f1	f2	f3	f4	f5	f6	f7
0 0	0	0	0	0	0	0	0	0
0 1	0	0	0	0	1	1	1	1
1 0	0	0	1	1	0	0	1	1
1 1	0	1	0	1	0	1	0	1
Обозначение	0	x1x2		x1		x2	x1x2	x1x2

Продолжение табл.1.3

x1, x2\ f	f8	f9	f10	f11	f12	f13	f14	f15
0 0	1	1	1	1	1	1	1	1
0 1	0	0	0	0	1	1	1	1
1 0	0	0	1	1	0	0	1	1
1 1	0	1	0	1	0	1	0	1
Обозначение	x1x2	x1 ~ x2				x1  x2	x1x2	1

Важнейшими из них являются: — конъюнкция (x₁ x₂, x₁ & x₂, x₁x₂), — сложение по модулю 2 (x₁x₂), — дизъюнкция (x₁x₂), — функция Пирса (x₁x₂), — импликация (x₁x₂), — функция Шеффера (x₁| x₂).

Определение 1.4. Переменная x_i, или i-я переменная двоичной функции f(x₁, ..., x_n) называется существенной переменной функции f (т.е. функция f существенно зависит от x_i), если существует набор (a₁, ..., a_i-1, a_i+1, ..., a_n) , такой, что

f(a₁, ..., a_i-1, 0, a_i+1, ..., a_n)  f(a₁, ..., a_i-1, 1, a_i+1, ..., a_n).

В противном случае переменная x_i называется несущественной (фиктивной) переменной функции f.

Так, среди функций от двух переменных имеется ровно десять функций, существенно зависящих от всех своих переменных.

Число двоичных функций от n переменных растет с увеличением n чрезвычайно быстро. В табл.1.4 приведена зависимость функций от своих переменных при n  8.

Таблица 1.4

n	Число функций от n переменных
1	2
2	16
3	256
4	65536
5	4294967296
6	> 1.8 10^19
7	> 3.4 10^38
8	> 1.1 10^77

С табличным заданием функции непосредственно связан такой ее параметр, как вес.

Определение 1.5. Множество двоичных наборов {(a₁, ..., a_n)  |f(a₁, ..., a_n) = 1}, на которых функция f принимает значение 1, называется областью истинности функции f. Мощность области истинности функции f называется весом функции f и обозначается || f ||.

Очевидно, что 0  || f ||  2ⁿ, причем равенства достигаются лишь для функций-констант 0 и 1. Если || f || = 2^n-1, то функция f называется равновероятной.

Для двоичных функций используются и другие способы задания, приспособленного для рассматриваемой в каждом конкретном случае задачи, которые будут рассмотрены далее.