3.3. Критерий полноты системы булевых функций

Теорема 3.27. Система булевых функций полна тогда и только тогда, когда она содержит хотя бы по одной функции каждого из следующих классов:

, ,,,

(без доказательства).

Пример 3.28. Пусть функция задана табл.3.3.

Таблица 3.3

0	0	0	1
0	0	1	0
0	1	0	0
0	1	1	0
1	0	0	0
1	0	1	0
1	1	0	0
1	1	1	0

Показать, что  — шефферова функция, т.е. — полная система, т.е.. Выразитьиформулами надК.

Решение:

,

но не

.

Чтобы выяснить вопрос о принадлежности классу, представиммногочленом Жегалкина:

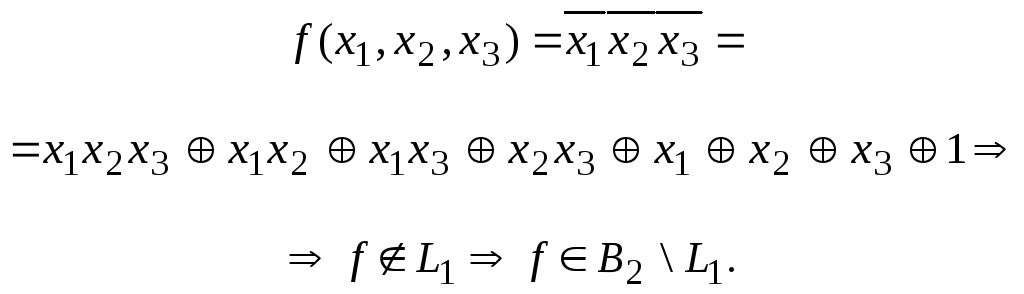
Итак, все условия теоремы 3.27 выполнены. Следовательно — полная система, т.е.— шефферова функция.

Теперь решим вторую часть примера. Так как , то очевидно,.

Л е к ц и я 4

4.1. Псевдобулевы функции

Пусть Р — произвольное поле. Элементы будем рассматривать как нуль и единицу поля.

Определение 4.1. Псевдобулевой функцией от переменных, или-местной псевдобулевой функцией, над полемР при называется любое отображениевР. Нуль-местными псевдобулевыми функциями над Р называются все элементы поля Р.

Множество всех пседобулевых функций от переменных над полемР обозначим через . В частности, прикласссовпадает с классом булевых функций. В других случаях эти классы различны, и если условиться псевдобулеву функцию со значением изсчитать булевой, то. Множество функцийотносительно естественным образом определяемых операций сложения функций и умножения функций на элементы изР образуют линейное пространство над полем Р.

Рассмотрим систему функций:

, (4.1)

где — символ Кронекера, т.е.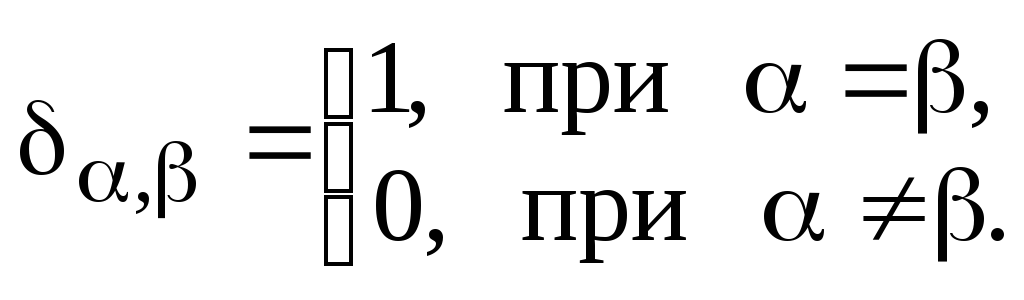

Утверждение 4.2. Система функций (4.1) является базисом пространства .

Доказательство. Очевидно, что система (4.1) — линейно независимая система. Далее пусть — произвольная функция из. Тогда очевидно, что

. (4.2)

Отсюда следует, что (4.1) — базис пространства .

Замечание 4.3. Если , то— булева функция и разложение (4.2) функциисовпадает с разложением, полученным заменой в её СДНФ операциина.

Замечание 4.4. Если , то система функций

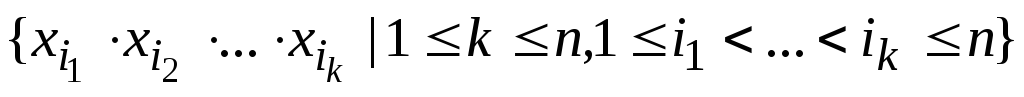(4.3)

является базисом пространства . Это следует из теоремы 2.15 об однозначном представлении булевых функций многочленами Жегалкина. В этом случае представление функции многочленом Жегалкина есть (4.3).

Замечание 4.5. Представление булевых функций через базисы пространства сопряжено со многими трудностями. Вот две из них:

непростым является вопрос об описании базисов пространства ;

если даже имеется система функций, являющаяся базисом пространства, то в общем случае сложным является вопрос о нахождении коэффициентов в разложении булевой функции по указанному базису.

Замечание 4.6. В решении вопроса об описании базисов пространства иногда оказывается полезным переход от пространствак пространствувекторов-столбцов длинынад полемР. Сопоставим каждой функции вектор столбец значенийэтой функции. В итоге получаем отображениепространствав пространство. Нетрудно видеть, чтоесть изоморфизм пространств, а поэтому система функцийявляется базисом пространстватогда и только тогда, когда матрицаявляется невырожденной.