2. Нумерация мпд-программ

Приведем аналогичную конструкцию по нумерации МПД-программ, которая позволит получить нумерацию МПД-вычислимых функций. Сначала определим нумерацию команд. Положим

(Z(n)) = 4(n – 1),

(S(n)) = 4(n – 1) + 1,

(T(m, n)) = 4p(m – 1, n – 1) + 2,

(J(m, n, q)) = 4(m, n, q) + 3,

где p(x, y) = 2^x(2y + 1) – 1, (x, y, z) = p(p(x – 1, y – 1), z – 1).

Ясно, что функция  эффективно вычислима. Для вычисления действуем так:

Находим числа u, v, такие, что x = 4u + v, где . Тогда имеем:

= Z(u + 1), если v = 0;

= S(u + 1), если v = 1;

= T(l(u) + 1, r(u) + 1), если v = 2;

= J(m, n, q), если v = 3, где (m, n, q) = .

Следовательно, функция также эффективно вычислима.

Пусть теперь дана МПД-программа P = I₁. . .I_s. Определим ее номер (Р) = ((I₁), …, (I_s)), где

(x₁, …, x_s) = .

Ясно, что тем самым определена биекция  множества программ в множество натуральных чисел, причем функции  и ^-1 эффективно вычислимы, по программе Р эффективно находится ее номер n = (P), а по номеру n можно эффективно найти программу Р такую, что n = (P). Число (P) называется номером программы Р. Например, если Р = I₁I₂I₃, где I₁ = T(3, 1), I₂ = S(4), I₃ = Z(6), то

(T(3, 1)) = 18, (S(4)) = 13, (Z(6)) = 20.

Следовательно, (P) = 2¹⁸2³²2⁵³ – 1. Пусть теперь дано n = 4127. Поскольку 4127 = 2⁵ + 2¹² – 1, то Р = I₁I₂, где (I₁) = 5, (I₂) = = 18 – 5 – 1. Следовательно, I₁ = S(2), I₂ = T(2, 1).

Разумеется, существуют и другие способы нумерации программ, для нас важна лишь эффективная вычислимость функций  и ^-1.

Таким образом, получаем эффективную нумерацию МПД-программ:

P₀, P₁, P₂, …, P_n, … .

Теперь, имея нумерацию МПД-программ, можно занумеровать МПД-вычислимые функции. Для любого a  N и n  1 определим n-местная функция, вычислимая программой с номером а. Это дает нумерацию n-местных МПД-вычислимых функций ,,, …

Например, если а = 4127, то согласно определению имеем:

, n = 1;

, n > 1.

Поскольку для всякой частично рекурсивной функции существует вычисляющая ее МПД-программаР, то , гдеa = (P). Число а называют номером (индексом) функции .

Приведем одно применение существования нумерации частично рекурсивных функций.

Теорема 15.2. Существует всюду определенная функция, не являющаяся частично рекурсивной.

Доказательство. Построим всюду определенную функцию , отличающуюся от каждой частично рекурсивной функции f₀, f₁, …, f_n, … в перечислении одноместных частично рекурсивных функций. Полагаем

Функция  всюду определена и отличается от f_n при x = n, n  N₀. Действительно, если f_n(n) определено, то (n) = f_n(n) + 1, если f_n(n) не определено, то (n) определено и равно 0. Поскольку  отличается от f_n при всех n  N₀, то  не может находиться в перечислении (10) и, значит, она не может быть частично рекурсивной, что и требовалось доказать.

Замечание. 15.3. Приведенный метод рассуждения есть пример диагональной конструкции Кантора, с помощью которой им была доказана несчетность множества действительных чисел. Данным методом можно установить нерекурсивность большого класса функций.

Например, функция

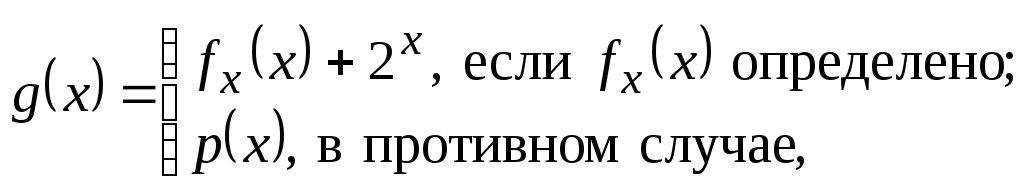
причем p(x) — целочисленный полином является всюду определенной и не частично рекурсивной.