6.1. Метод Квайна — Мак-Класки нахождения сокращённой днф двоичной функции

Пусть функция f задана в виде СДНФ. Метод, предложенный Квайком в 1952 г. заключается в следующем:

1) применим к элементарным конъюнкциям СДНФ операцию «неполного склеивания»: , до тех пор, пока в результате применения этой операции не перестанут появляться новые конъюнкции;

2) в полученной ДНФ выполняем операции поглощения: , пока это возможно.

Теорема 6.1. В результате выполнения пунктов 1, 2 получается сокращённая ДНФ функции f.

Доказательство. Сначала заметим, что из всякой импликанты функции f можно с помощью «операции расклеивания» получить дизъюнкцию импликант длиныn. Поскольку все импликанты длины n входят в СДНФ, то в результате применения операции неполного склеивания в СДНФ на первом этапе (пункт 1) метода будут получены все, в том числе и простые, импликанты функции f.

После применения второго этапа (пункт 2), очевидно, в ДНФ останутся только простые импликанты, т.е. полученная в результате ДНФ будет сокращенной. Теорема доказана.

Мак-Класки в 1956 г. предложил удобную интерпретацию этого метода. Прежде всего заметим, что склеиваться могут только конъюнкции одинакового ранга, отличающиеся по одной переменной. Будем записывать конъюнкции в виде вектора ().Индексом конъюнкции назовём .

Учитывая это замечание, разобьём все импликанты в СДНФ на группы в соответствии со значениями их индексов. Сам метод при этом заключается в заполнении таблицы специального вида (табл.6.1).

Таблица 6.1

Индекс	СДНФ	Шаг 1	Шаг 2	Шаг 3
1	1000*	1_00* 10_0*	1__0	______
2	1100* 1010* 0101* 0011*	11_0* 1_10* 101_ 01_1 _011 0_11	______	______
3	1110* 1011* 0111*	______	______	______

Пример 6.2. Пусть f — функция, геометрическое представление которой дано на рис.5.1. Её СДНФ имеет вид:

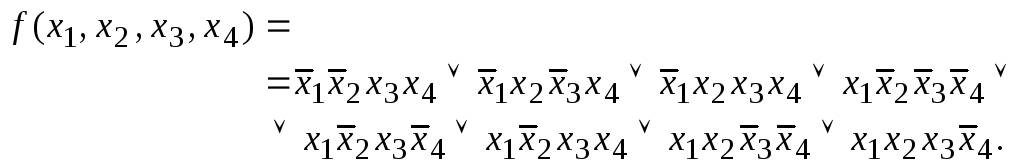
Применяя операцию неполного склеивания к импликантам длины n (СДНФ) производим заполнение колонки табл.6.1. При этом в СДНФ звёздочкой отмечаются использованные импликанты (они будут поглощаться на втором этапе). Затем операция склеивания применяется к конъюнкциям ранга (n – 1) и т.д. Как только заполнение таблицы прекратилось, выбираются все не отмеченные звёздочкой импликанты и из них составляется сокращённая ДНФ. Для рассмотренного примера сокращённой ДНФ будет:

6.2. Метод нахождения тупиковых днф

Для изложения метода нахождения тупиковых ДНФ нам потребуется одно свойство ДНФ монотонных функций.

Утверждение 6.3. Минимальная ДНФ монотонной функции совпадает с её сокращённой ДНФ.

Доказательство. Сначала покажем, что все простые импликанты монотонной функции не содержат переменных с отрицаниями. Действительно, в противном случае наряду с простой импликантой функция имела бы импликанту(в силу её монотонности). Склеивая эти две импликанты, получаем противоречие с простотой импликанты.

Покажем теперь, что все простые импликанты входят в минимальную ДНФ. Пусть — простая импликанта. Тогда на набореимпликантапринимает значение 1. Все остальные импликанты должны быть равны на этом наборе нулю, так как в них обязательно должны входить переменные из множества. Следовательно,импликанта должна входить в минимальную ДНФ, поскольку иначе функцияf на этом наборе будет равна 0. Утверждение доказано.