
- •Ф.К. Алиев, и.А. Юров
- •Введение
- •Основные способы задания двоичных функций
- •1.1. Табличный способ задания
- •1.2. Геометрический способ задания
- •1.3. Задание двоичных функций формулами
- •Основные способы задания двоичных функций (продолжение)
- •2.1. Нормальные формы двоичных функций
- •2.2. Многочлен Жегалкина и действительный многочлен двоичной функции
- •2.3. Теорема о разложении в ряд Фурье
- •Полнота и замкнутость. Критерий полноты системы. Функционально полные системы. Замкнутые классы булевых функций
- •3.1. Полнота и замкнутость. Функционально полные системы
- •3.2. Замкнутые классы булевых функций
- •3.3. Критерий полноты системы булевых функций
- •4.1. Псевдобулевы функции
- •4.2. Функции k-значной логики
- •5.1 Минимизация двоичных функции
- •5.2. Геометрическая интерпретация минимизации днф
- •6.1. Метод Квайна — Мак-Класки нахождения сокращённой днф двоичной функции
- •6.2. Метод нахождения тупиковых днф
- •6.3. Метод Петрика нахождения тупиковых днф
- •Алгебраические системы
- •7.1. Алгебраические системы. Булевы алгебры
- •7.2. Изоморфизм алгебраических систем
- •Алгебры высказываний. Предикаты и операции над ними
- •8.1. Основные логические операции и их свойства
- •8.2. Предикаты и операции над ними
- •Исчисление предикатов
- •9.1. Общее понятие о логическом исчислении
- •9.2. Формулы алгебры предикатов
- •9.3. Равносильность формул. Основные отношения равносильности
- •9.4. Использование равносильностей для упрощения формул
- •9.5. Построение исчисления предикатов
- •9.6. Выводимость и доказуемость формул
- •9.7. Семантика исчисления предикатов
- •Понятие о теории моделей
- •Элементы теории алгоритмов
- •11.1. Основные требования к алгоритмам
- •11.2. Машина Тьюринга и функции, вычислимые по Тьюрингу
- •11.3. Машины произвольного доступа и вычислимые функции
- •Частично рекурсивные функции и их вычислимость
- •Вычислимость суперпозиции
- •Вычислимость рекурсии
- •Вычислимость минимизации
- •Нумерация наборов чисел и слов
- •Нормальные алгоритмы
- •Нумерация алгоритмов
- •1. Нумерация машин Тьюринга
- •2. Нумерация мпд-программ
- •Универсальные функции
- •Алгоритмически неразрешимые проблемы
- •16.1. Алгоритмически неразрешимые проблемы
- •16.2. Примечательные алгоритмически неразрешимые проблемы
- •Характеристики сложности вычислений
- •Характеристика сложности вычислительных задач
- •18.1. Классы сложности p и np и их взаимосвязь
- •18.3. Основные np-полные задачи. Сильная np-полнота
- •Список Литературы
9.7. Семантика исчисления предикатов
Для уяснения смысла аксиом и правил вывода введем понятие интерпретации языка и исчисления α.
Определение 9.25. Под интерпретацией языка исчисления α понимают любое множество М с зафиксированным отображением сигнатуры σ во множество операций и предикатов, определенных на М, при котором символу n-арной операции f из σ соответствует n-арная операция f, определенная на множестве М, а символу n-арного предиката р из σ n-арный предикат р на М. Образ множества σ при отображении обозначим через σ. В частности, образом констант из σ при будут нуль-арные операции на М, т. е. некоторые элементы из М.
Если (М, ) — интерпретация языка α, то, заменив в любой формуле языка α константы, символы операций и символы предикатов их образами при и условившись переменным из Х придавать значения из множества М, мы получим формулу А алгебры предикатов на алгебраической системе М(σ), и можно говорить о выполнимости, истинности или ложности этой формулы на системе М(σ).
Определение 9.26. Формула А исчисления предикатов называется выполнимой, истинной, ложной в интерпретации (М, ), если соответственно выполнима, истинна, ложна формула А на алгебраической системе М(σ).
Определение 9.27. Формула А исчисления предикатов α называется тождественно истинной, если она истинна во всех интерпретациях исчисления α.
Естественно возникает вопрос о соотношении между классами доказуемых и истинных формул исчисления предикатов. Ответ на этот вопрос можно получить из следующих теорем.
Теорема 9.28. Если каждая формула множества формул Т истинна в некоторой интерпретации (М, ) исчисления α и T├─ A, то А — истинна в (М, ).
Доказательство. Для простоты записей условимся считать, что операции и предикаты на М обозначены теми же буквами, что и соответствующие им символы операций из σ. Тогда — тождественное отображение и в записи А индекс можно опускать.
Из определения доказуемой формулы следует, что достаточно доказать два утверждения:
а) все аксиомы истинны;
б) формула, являющаяся непосредственным следствием по любому правилу вывода из истинных формул, является истинной.
Истинность аксиом первых четырех групп аксиом доказывается одним методом. Проиллюстрируем его на аксиоме I1: A (B A).
Заменив в А, В свободные вхождения переменных элементами из М, получим высказывания, имеющие вполне определенные значения £ и ß (каждое из £, ß есть «и» или «л»). Перебирая всевозможные наборы значений «и» и «л» для £, ß мы непосредственной проверкой (пользуясь определением операции ) убедимся в том, что при любых £, ß £ (ß £) и.
Отсюда следует, что аксиома I1 истинна в интерпретации (М, ).
Докажем теперь истинность аксиомы
V1 : x A(x) A(t),
где t — терм, свободный для х в А(х). Пусть х, х1, …, хn суть все переменные, имеющие свободные вхождения в А(х) и xi1, …, xim — все переменные, участвующие в образовании терма t. Так как t свободен для х в А(х), то все вхождения переменных xi1, …, xim в терм t останутся свободными при подстановке t вместо х в формулу А(х). В связи с этим запишем:
A(t) = A(t(xi1, …, xim), х1, …, хn).
Допустим, что формула V1 не истинна в интерпретации (М, ). Это означает, что при некотором наборе значений переменных х1 = a1, …, хn = an, xi1 = ai1, …, xim = aim формула x A(x) принимает значение «и», а формула A(t) — значение «л». Если обозначить через b значение терма t при xi1 = ai1, …, xim = aim, то будем иметь: с одной стороны, A(х0, a1, …, an) является истинным высказыванием при любом значении х0 М, а с другой стороны, высказывание A(b, a1, …, an) — ложно. Полученное противоречие и доказывает наше утверждение.
Аналогично доказывается, что правила вывода позволяют из истинных формул в интерпретации (М, ) получать снова истинные формулы, т.е.:
1) если истинны формулы А и А В, то истинна и формула В;
2) если истинна формула В А(х) и х не имеет свободных вхождений в В, то истинна формула В х А(х);
3) если истинна формула А(х) В и х не имеет свободных вхождений в В, то истинна и формула х А(х) В.
Теорема доказана.
Следствие 9.29. Всякая доказуемая формула исчисления предикатов α является истинной в любой интерпретации (М, ) исчисления α.
Замечание. Теорема и следствие теряют силу, если в аксиомах V1 и V2 не накладывать ограничений на терм t или в правилах -введения и -удаления разрешить свободные вхождения х в В. Приведем соответствующие примеры.
1. Пусть множество натуральных чисел N, A(x) = y (x < y) и t = x + y — терм, не свободный для х в А(х), поскольку свободное вхождение буквы х в А(х) находится в области действия квантора по букве у, входящий в терм t. Нетрудно видеть, что формула x A(x) A(t), или подробнее, x(y(x < y)) y(x + y < y) ложна в арифметике.
2. В той же интерпретации, положим B = (x y), A = (x y + 1). Тогда имеем: формула В А истинна на N, а формула В xА ложна, поскольку, например, при х = 2, у = 3 имеем (2 3) и, x (x 4) л.
Доказанная теорема свидетельствует о том, что логические средства исчисления предикатов выбраны разумно, поскольку с их помощью можно доказать только утверждения, истинные с содержательной точки зрения.
Следствие
9.30. Исчисление
предикатов непротиворечиво, т.е. в нем
не может быть доказуемой никакая формула
А
вместе с ее отрицанием, или никакая
формула вида
![]() .
.
Действительно
формула
![]() является ложной в любой интерпретации,
тогда как доказуемые формулы истинны
в любой интерпретации.
является ложной в любой интерпретации,
тогда как доказуемые формулы истинны
в любой интерпретации.
Теперь естественно возникает вопрос: не слишком ли мало аксиом и правил вывода мы взяли при построении исчисления предикатов? Так, из доказательства предыдущей теоремы видно, что если бы нашлась формула А, не доказуемая в исчислении предикатов, но истинная в любой его интерпретации, то, присоединив А к системам аксиом, мы получили бы более сильное и непротиворечивое логическое исчисление. Однако ниже будет показано, что такой формулы А не существует, а именно имеет место следующая теорема Геделя о полноте исчисления предикатов.
Теорема 9.31. Если формула исчисления предикатов истинна во всех его интерпретациях, то она доказуема в исчислении предикатов.
Для доказательства этой теоремы введем сначала некоторые понятия и докажем одно общее утверждение (см. теорему 9.7.11).
Определение
9.32. Множество
формул Т
исчисления α называется противоречивым,
если существует такая формула А
языка α, что Т├─
![]() .
В противном случаеТ
называется непротиворечивым.
.
В противном случаеТ
называется непротиворечивым.
Определение 9.33. Множество формул Т исчисления α называется выполнимым, если существует интерпретация, в которой все формулы из Т принимают истинное значение хотя бы при одной (общей для всех формул из Т) замене переменных.
Определение
9.34. Множество
формул Т
исчисления α называется полным,
если для каждой замкнутой формулы языка
α имеет место Т├─
А
или Т
├─
![]() .
.
Теорема 9.35. Всякое непротиворечивое множество S замкнутых формул исчисления α выполнимо.
Доказательство. Добавим к множеству символов языка α еще счетное множество констант (символов нуль-арных операций) ß = {b0, b1, b2, …}.
Получим
новый язык α1
в сигнатуре σ1 = σ ß.
Заменяя в аксиомах и правилах вывода
исчисления α формулы языка α1,
мы получим новое логическое исчисление,
которое обозначим той же буквой α1.
Из определения языка α1
видно, что все доказанные факты об
исчислении α (в частности, все доказанные
формулы и дополнительные правила вывода)
сохраняются и в α1.
Так как язык α1
включает в себя α, то S
можно рассматривать как множество
предложений языка α1.
Легко видеть, что S
будет непротиворечивым и в исчислении
α1.
Действительно, если в α1
из S
выводима формула
![]() ,
то, заменив в формулах вывода
,
то, заменив в формулах вывода![]() изS
все константы из ß переменными, не
участвующими в этом выводе, мы получим
вывод в α из S
формулы
изS
все константы из ß переменными, не
участвующими в этом выводе, мы получим
вывод в α из S
формулы
![]() ,
гдеВ
получается из А
указанной заменой констант. Чтобы
убедиться в этом, достаточно заметить,
что указанная замена аксиомы переводит
в аксиомы и сохраняет свойство формулы
быть непосредственным следствием
предыдущих формул. Таким образом, S
непротиворечиво в α1.
,
гдеВ
получается из А
указанной заменой констант. Чтобы
убедиться в этом, достаточно заметить,
что указанная замена аксиомы переводит
в аксиомы и сохраняет свойство формулы
быть непосредственным следствием
предыдущих формул. Таким образом, S
непротиворечиво в α1.
Теперь расширим определенным образом множество S. Для этого занумеруем все замкнутые формулы исчисления α1: А0, А1, А2, …
По формуле А0 и системе S построим множество формул S0, положив:
 где
bi0 —
символ с наименьшим номером из ß, не
встречающийся в А0.
Из определения S0
имеем: S S0
и S0
├─ А0
или S0
├─
где
bi0 —
символ с наименьшим номером из ß, не
встречающийся в А0.
Из определения S0
имеем: S S0
и S0
├─ А0
или S0
├─
![]() .
.
Покажем,
что S0
непротиворечиво. Допустим, что в α1
S0 ├─ ![]() .
В соответствии с определениемS0
рассмотрим три случая.
.
В соответствии с определениемS0
рассмотрим три случая.
1. S
├─ А0.
Тогда S0 = S {![]() }
и из (9.5) имеем:S,
А0 ├─
}
и из (9.5) имеем:S,
А0 ├─![]() .
Отсюда по следствию из теоремы дедукции
получаемS
├─
.
Отсюда по следствию из теоремы дедукции
получаемS
├─
![]() ,
что невозможно в силу непротиворечивостиS.
,
что невозможно в силу непротиворечивостиS.
2. ![]() невыводима изS
и А0
не имеет вида х
В0(х).
Тогда S0 = S {А0}
и мы точно так же, как и в случае «а»,
получим S ├─
невыводима изS
и А0
не имеет вида х
В0(х).
Тогда S0 = S {А0}
и мы точно так же, как и в случае «а»,
получим S ├─ ![]() ,
что противоречит условию.
,
что противоречит условию.
3. ![]() невыводима изS
и А0 = х
В0(х).
Тогда S0 =
= S {А0, B0, (bi0)},
и потому S,
А0,
B0,
(bi0)
├─
невыводима изS
и А0 = х
В0(х).
Тогда S0 =
= S {А0, B0, (bi0)},
и потому S,
А0,
B0,
(bi0)
├─
![]() .
Так как формулаB0
(bi0)
замкнута, то тем же приемом, что и выше,
получим S,
А0
├─
.
Так как формулаB0
(bi0)
замкнута, то тем же приемом, что и выше,
получим S,
А0
├─
![]() .
Так как bi0
не входит в А0
и в формулы из S,
то, повторив весь вывод с заменой bi0
на переменную xJ,
не входящую в участвующие в выводе
формулы, мы получим S,
А0
├─
.
Так как bi0
не входит в А0
и в формулы из S,
то, повторив весь вывод с заменой bi0
на переменную xJ,
не входящую в участвующие в выводе
формулы, мы получим S,
А0
├─
![]() ,
илиS
├─ А0
,
илиS
├─ А0
![]() .
Дополним выводА0
.
Дополним выводА0 ![]() изS
формулами:
изS
формулами:
|
А0 xj |
(правило -введения) |
|
xj |
(аксиома) |
|
А0 |
(правило силлогизма) |
|
А0 x
|
(правило -введения) |
|
x |
(правило -отрицания) |
|
А0 |
(правило силлогизма) |
Поскольку
xB0(x) = А0,
то мы получили вывод из S
формулы А0 ![]() ,
т.е.S,
А0├─
А0.
А так как S,
А0
├─ А0,
то по правилу умножения формул S,
А0├─
А0
,
т.е.S,
А0├─
А0.
А так как S,
А0
├─ А0,
то по правилу умножения формул S,
А0├─
А0![]() .
Отсюда следует:S├─
А0,
и мы снова пришли к противоречию с
условием. Тем самым мы закончили
доказывать непротиворечивость множества
формул S0.
.
Отсюда следует:S├─
А0,
и мы снова пришли к противоречию с
условием. Тем самым мы закончили
доказывать непротиворечивость множества
формул S0.
Далее,
по А1
и S0
мы аналогично построим непротиворечивое
множество S1
такое, что: S0 S1,
S1├─
А1
или S1├─
![]() .
.
Продолжая
этот процесс, мы получим последовательность
непротиворечивых множеств формул
S0 S1 S2 …
таких, что Si├─
Аi
и Si├─![]() .
Следовательно,
.
Следовательно,![]() есть
непротиворечивое и полное множество
формул.
есть
непротиворечивое и полное множество
формул.
Теперь построим интерпретацию исчисления предикатов α, в которой истинны все формулы из α. В качестве основного множества возьмем множество М термов языка α1, в которых нет предметных переменных — это так называемые замкнутые термы языка α1. Определим на М операции f и предикаты р, соответствующие символам операций f и предикатов р из α.
Если а — символ 0-арной операции из σ, то положим а = а. Если f — символ n-арной операции из σ, p — символ n-арного предиката и t1, …, tn — термы из М, то положим f (t1, …, tn) = f(t1, …, tn):
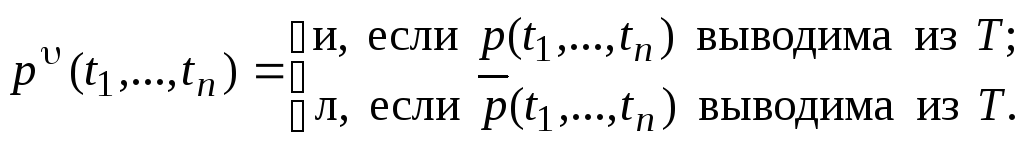
Тем самым определена интерпретация (М, σ) исчисления α1, а потому и α.
Теперь индукцией по рангу формулы А докажем, что для любой замкнутой формулы языка α1:
Т├─ А в α1 А и в (М, σ). (9.7)
Для упрощения записи верхний индекс у формул будем опускать. Если А = р(t1, …, tn) — элементарная формула, то (9.7) верно по определению предиката р.
Пусть А — замкнутая формула ранга r > 0. В зависимости от последней операции в А возможны шесть случаев.
1. А = А1А2. Используя определение конъюнкции, предположение индукции и правила умножения и разделения формул, получим: А и А1 = и, А2 = и Т├─ А1, Т├─ А2 Т├─ А1А2.
2. А = А1 А2.
Если А1 А2 и,
то А1 = и
или А2 = и.
Тогда по предположению индукции Т├─
А1
или Т├─
А2,
а поэтому и Т├─ А1 А2.
Обратно, пусть Т├─
А1 А2.
Если Т├─
А1
или Т├─ А2,
то по предположению индукции А1 и
или А2 и,
а потому и А и.
В противном случае, в силу полноты
системы Т
имеем: Т├─![]() ,Т├─
,Т├─
![]() .
Тогда по правилам умножения формул и
де Моргана получим:Т├─
.
Тогда по правилам умножения формул и
де Моргана получим:Т├─ ![]() ,Т├─
,Т├─ ![]() .
Итак, имеем:Т├─ А1 А2,
Т├─
.
Итак, имеем:Т├─ А1 А2,
Т├─
![]() ,
что невозможно в силу непротиворечивостиТ.
,
что невозможно в силу непротиворечивостиТ.
3. А =А1. Учитывая предположение индукции и полноту системы формул Т, получим: А и А л Т├─ А1 Т├─ А.
4. А = А1 А2. В этом случае, используя предположение индукции и правила введения посылки, контрапозиции и двойного отрицания, получим: А и А1 л или А2 и Т├─ А1, или Т├─ А2 Т├─ А2 А1 или Т├─ А2 А1 Т├─ А.
5. А = хА1(х).
Если А и,
то А1(t) и
при любом t M.
Тогда по предположению индукции Т├─
А1(t)
для всех t M.
Допустим, что T
├─![]() .
Тогда по правилу-отрицания
T
├─
.
Тогда по правилу-отрицания
T
├─
![]() и по построению множестваТ
в Т
существует формула
и по построению множестваТ
в Т
существует формула
![]() при некоторой константеb M.
В итоге мы получили: Т├─
А1(t)
при любом t M
и Т├─
А1(b)
при b M,
что невозможно в силу непротиворечивости
Т.
Следовательно, T
├─ хА1(х).
Обратно, пусть T ├─
хА1(х).
Если хА1(х) и,
то А1(t) л
при некотором t M.
Тогда по предположению индукции Т├─
при некоторой константеb M.
В итоге мы получили: Т├─
А1(t)
при любом t M
и Т├─
А1(b)
при b M,
что невозможно в силу непротиворечивости
Т.
Следовательно, T
├─ хА1(х).
Обратно, пусть T ├─
хА1(х).
Если хА1(х) и,
то А1(t) л
при некотором t M.
Тогда по предположению индукции Т├─
![]() .
Отсюда по аксиомеV2
и по правилу -отрицания
получим T
├─
.
Отсюда по аксиомеV2
и по правилу -отрицания
получим T
├─
![]() иT ├─
иT ├─ ![]() ,
что невозможно в силу непротиворечивостиТ.
,
что невозможно в силу непротиворечивостиТ.
6. А = хА1(х).
Если А и,
то А1(t) и
при некотором t M
и по предположению индукции Т├─
А1(t).
Отсюда, используя аксиому V2,
получим T
├─ хА1(х),
т.е. Т├─
А.
Обратно, если Т├─
А,
то в силу непротиворечивости Т
получим, что
![]() не выводима изТ.
Тогда, по построению Т,
в Т
содержится формула А1(b)
при некотором b M.
По предположению индукции А1(b) и,
а потому и хА1(х) = и.
не выводима изТ.
Тогда, по построению Т,
в Т
содержится формула А1(b)
при некотором b M.
По предположению индукции А1(b) и,
а потому и хА1(х) = и.
Таким образом, все замкнутые формулы языка α, выводимые из Т, истинны в интерпретации (М, ). А так как S T, то и все формулы из S истинны в (М, ), т.е. множество S выполнимо и теорема доказана.
Теперь
можно доказать и теорему Гёделя о полноте
исчисления α. Пусть А —
формула исчисления предикатов α и А и
в любой интерпретации исчисления α.
Если х1, …, хn
суть все переменные, имеющие свободные
вождения в А,
то формула В = х1, …, хnА
также истинна в любой интерпретации α,
а потому формулаВ
ложна в любой интерпретации α. Отсюда
следует, что множество формул
![]() невыполнимо.
невыполнимо.
Тогда
по теореме о выполнимости множество
![]() противоречиво, т.е. существует формулаС
языка α, такая, что
противоречиво, т.е. существует формулаС
языка α, такая, что
![]() ├─
├─![]() .
.
Но тогда по следствию из теоремы дедукции ├─ B. Теперь, применяя n раз аксиому V1 и правило заключения, получим ├─ A, что и доказывает теорему Гёделя.
В качестве других следствий теоремы о выполнимости докажем так называемую теорему о совместной выполнимости и локальную теорему Мальцева.
Теорема 9.36 (о совместной выполнимости). Если замкнутая формула А исчисления α истинна в любой интерпретации α, в которой истинны формулы некоторого Т замкнутых формул, то Т├─ А.
Доказательство.
Из условия видно, что множество формул
![]() Т
U
Т
U ![]() невыполнимо. Значит, по теореме о
выполнимости множество
невыполнимо. Значит, по теореме о
выполнимости множество
![]() противоречиво, т.е.T,
противоречиво, т.е.T, ![]() ├─
├─![]() для некоторой формулыВ.
Отсюда по следствию из теоремы дедукции
Т├─
А.
для некоторой формулыВ.
Отсюда по следствию из теоремы дедукции
Т├─
А.
Теорема Мальцева (9.37). Множество замкнутых формул S исчисления α выполнимо тогда и только тогда, когда выполнимо любое его конечное подмножество.
Доказательство.
Выполнимость конечных подмножеств
выполнимого множества формул очевидна.
Докажем обратное утверждение. Допустим,
что выполнимо любое конечное подмножество
формул множества S,
а само S
невыполнимо. Тогда по теореме о
выполнимости оно противоречиво, т.е.
найдется такая формула А,
что S├─
![]() .
.
Но
тогда
![]() выводима лишь из конечного подмножестваS1 S
формул, участвующих в выводе формулы
выводима лишь из конечного подмножестваS1 S
формул, участвующих в выводе формулы
![]() изS.
Следовательно, нашлось противоречивое
конечное множество формул из S.
Если бы S
было выполнимым, то по теореме 9.28 нашлась
бы интерпретация α, в которой была бы
истинной формула
изS.
Следовательно, нашлось противоречивое
конечное множество формул из S.
Если бы S
было выполнимым, то по теореме 9.28 нашлась
бы интерпретация α, в которой была бы
истинной формула
![]() ,
что невозможно. Полученное противоречие
и доказывает теорему.
,
что невозможно. Полученное противоречие
и доказывает теорему.
Л е к ц и я 10
