LibrEduMethodSectionsEditionsFilesDownload

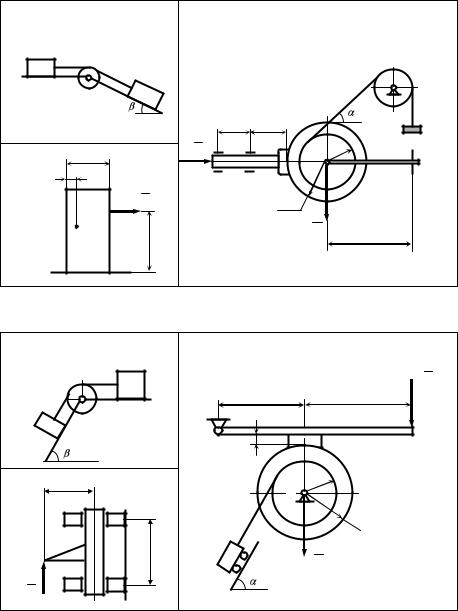
		Рисунки к заданию 4.17
1.		3.
A
		B
			a	b	Q
2.	ℓ	P		O	R
					С
	b
D	Е	A	B
		P		1,5R
	С	h		G	2b
A	B
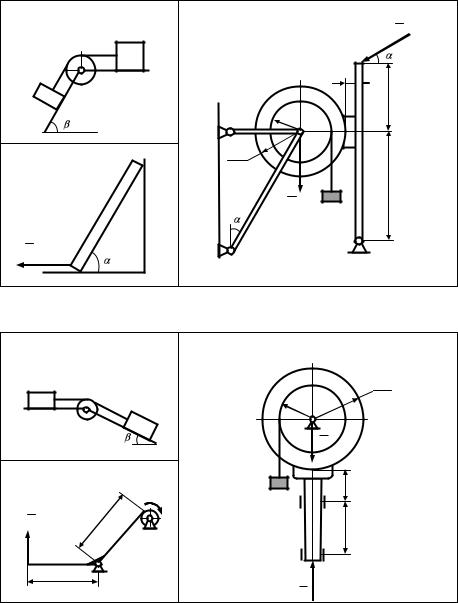
		Рисунки к заданию 4.18
1.		3.
		A
					P
			a		b
B
		A	е		B
2.	a			R
				O
	A
					1,4R
		Q
		h
C				G
P	B
	B
					121

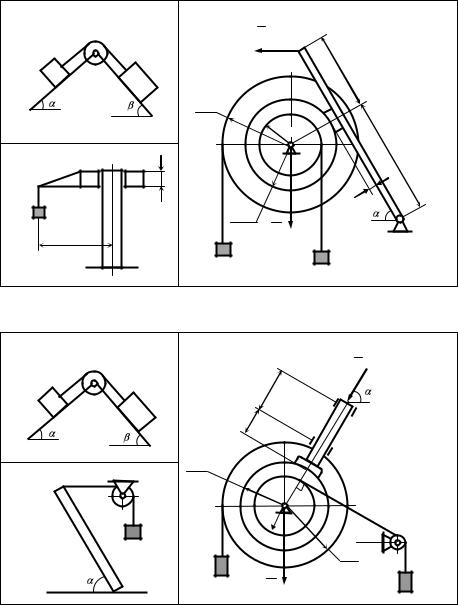
			Рисунки к заданию 4.19
1.			3.
		A			P
					B
B					е
					b
			C	R
2.			1,5R	O
		B
					a
				G	Q
P	A				A
			D
			Рисунки к заданию 4.20
1.			3.
A					1,8R
			B	R
				O
				G
2.			Q
					b
			M	B
		B
P	b
					a
A		O		A
	a
				P
					122

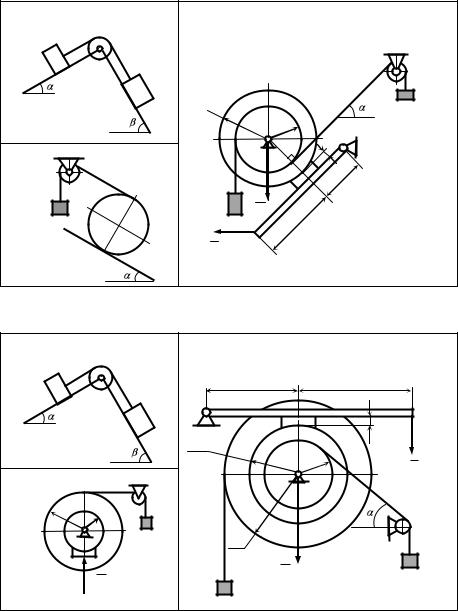
		Рисунки к заданию 4.21
1.		3.
		P	B
	B	A		a
		2R
			R O
2.				b
	A
	B	a		e
P		1,5R
	b		G	A
		Q		Q
		Рисунки к заданию 4.22
1.		3.
				P
	B	b
		A
		a		B
		1,2R		A
2.
	B		O
			R
		P
				2,5R
		Q
	A		G	Q
				123

Рисунки к заданию 4.23
1.	3.
A
B
	1,6R						Q
		O	R
2.					e	A
						a
P	Q	G	b
	P	B
Рисунки к заданию 4.24
1.	3.
A
		a				b
B	A						B
						e
	1,4R
			O	R			P
2.
R
r
P		2R
Q			G
	Q						Q
							124

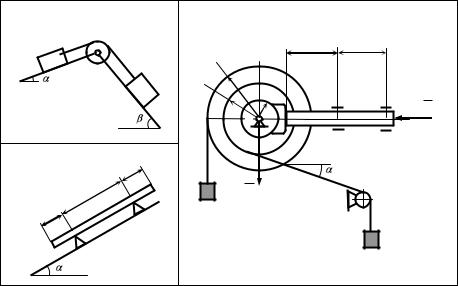
Рисунки к заданию 4.25
1.	3.
A	a	b
	2,5R
B	2R
	R
		P
	O
2.	B	A
b
a	G
b	Q
B
		Q
A

125

5РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ

Систему сил называют произвольной пространственной, если ли-

нии действия всех сил расположены произвольно в пространстве, т.е. не лежат в одной плоскости, не параллельны и не пересекаются в одной точке.

Для рассмотрения пространственных систем сил вводятся понятия векторного момента силы относительно центра, момента силы относительно оси.

mo ( F )

	h
А r	О

F

В

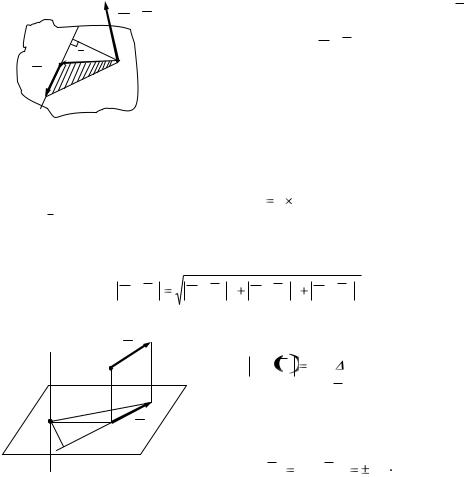
Рисунок 5.1

Векторным моментом силы F

относительно центра О называется, приложен-

ный в центре О вектор mo ( F ) , модуль кото-рого

равен произведению модуля F силы на еѐ плечо h, который направлен перпендикулярно плоскости, проходящей через центр О и силу в ту сторону, откуда видно стремление силы повернуть тело вокруг центра О против хода часовой стрелки.

Векторный момент силы относительно центра можно представить в виде векторного произведения (рисунок 5.1):

m	o ( F )			r	F ,			(5.1)

где r − радиус-вектор, проведѐнный из моментной точки О в точку приложения силы.

Модуль векторного момента (как и любого вектора) определяется через его проекции на координатные оси:

	mo ( F )		mo ( F ) 2	mo ( F ) 2		mo ( F ) 2 .		(5.2)
			x		y		z
Величина векторного момента силы относительно точки численно
		В	равна удвоенной площади треугольника ОАВ
	F		(2.2), т.е.:
z
	А			mO F		2 пл. OAB .
		В1	Моментом силы F				относительно оси
			называют		алгебраический момент проекции
O		FП	этой силы на плоскость П, перпендикулярную
h	А1		оси, относительно точки				пересечения	оси с
П			этой плоскостью (рисунок 5.2):
Рисунок 5.2				mz ( F )		mO ( FП )	FП h ,	(5.3)

126

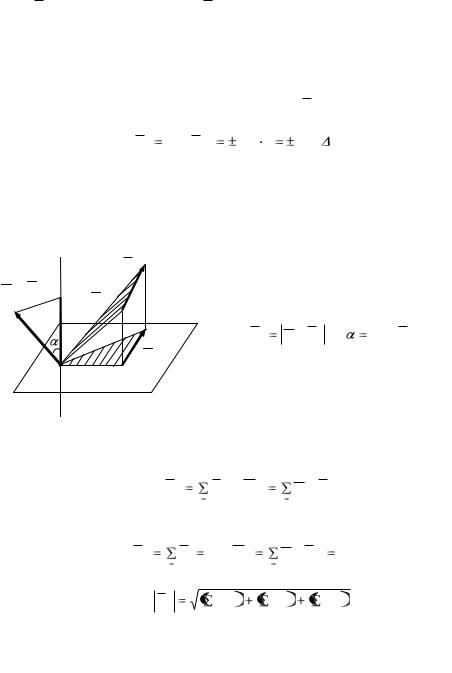
где FП − вектор проекции силы

F на плоскость П, перпендикулярную оси

Оz, а точка О − точка пересечения оси Оz с плоскостью П.

Момент силы относительно оси считается положительным, если сила

стремится поворачивать тело вокруг оси против хода часовой стрелки, если

смотреть с положительного направления оси.

Момент силы относительно оси можно выразить через площадь тре-

угольника ОА1В1, построенного на проекции силы FП и точке пересечения О

оси с плоскостью (рисунок 5.3):

mz ( F ) mo ( FП )

FП

h

2пл. OA1 B1 .

(5.4)

Из формулы (5.4) можно получить следующие свойства момента силы отно-

сительно оси:

1. Момент силы относительно оси равен нулю, если сила параллельна

оси.

2. Момент силы относительно оси равен нулю, если линия действия силы

пересекает эту ось.

z

F

Связь между моментом силы относи-

В

тельно оси и векторными моментами си-

mО ( F )

лы относительно точек, лежащих на этой

mz ( F )

оси (рисунок 5.3), определяется выраже-

А

нием:

В1

mz ( F )

mo ( F ) cos

moz ( F ),

(5.5)

O

FП

т.е. момент силы относительно оси равен

А1

проекции на эту ось векторного момента

П

силы относительно точки, лежащей на

оси.

Рисунок 5.3

Любая произвольная система сил при

приведении еѐ к произвольному центру

(см. стр. 35), приводится к одной силе, равной главному вектору, и паре сил,

момент которой равен главному моменту:

R*

n F ,

M*

n m

о

( F ) .

(5.6)

O

k

O

k

k

1

k 1

Для равновесия произвольной системы сил, необходимо и достаточ-

но, чтобы главный вектор и главный момент одновременно равнялись нулю:

R*

n F

0,

M*

n

m

о

( F )

0 .

(5.7)

O

k

O

k

k 1

k 1

Модуль главного вектора определяется:

R*

X

2

Y

2

Z

2 .

(5.8)

О

k

k

k

127

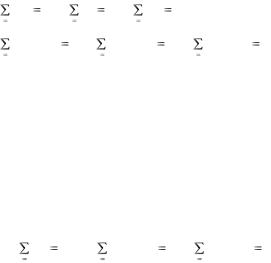
Учитывая выражения (5.2, 5.5, 5.7, 5.8) записываются аналитические условия равновесия произвольной пространственной системы сил:

n X k

0,

n Yk

0,

n Zk 0,

k

1

k 1

k 1

(5.9)

n mx (

n m

n

Fk ) 0,

у ( Fk ) 0,

mz ( Fk ) 0.

k

1

k 1

k

1

Для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций всех сил, приложенных к твердому телу, на оси декартовой системы координат, и алгебраические суммы моментов всех сил, относительно этих же осей, одновременно равнялись нулю.

Для равновесия пространственной системы параллельных сил необ-

ходимо и достаточно, чтобы алгебраическая сумма проекций всех сил на

одну из координатных осей, параллельную силам, и алгебраическая сумма моментов этих сил относительно двух других осей, одновременно равнялись нулю.

Например,

n		0 , то n mx (			n m у (
	Zk		Fk ) 0,			Fk ) 0 .		(5.10)
k	1	k 1			k 1

Задачи на равновесие тел, к которым приложена произвольная пространственная система сил, рекомендуется решать в следующей последовательности.

1.Уяснить содержание задачи и рисунок конструкции. Записать исходные данные и подлежащие определению величины.

2.Выделить тело, равновесие которого следует рассмотреть.

3.Показать на рисунке все активные силы, действующие на тело.

4.Определить типы связей и показать их реакции.

5.Убедиться в статической определимости задачи.

6.Составить уравнения равновесия полученной системы сил и решить их относительно величин, подлежащих определению.

7.Составить проверочное уравнение моментов активных и реактив-

ных сил.

Примечание – Во всех вариантах трением в шарнирных связях и блоках пренебречь.

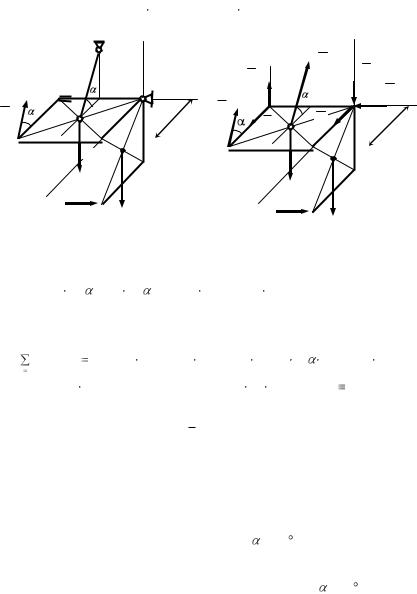
Пример 1. Жесткая конструкция, состоящая из двух одинаковых квадратных плит (АВВ1А1) и (ВВ1DD1) закреплена в точке В сферическим шарниром, в точке А цилиндрическим шарниром и удерживается в равнове-

128

сии стержнем СЕ. К конструкции приложены активные силы F1 , F2 , силы

тяжести плит Q1 , Q2 (рисунок 5.4).

Дано: F1 = F2 = 2 кН, Q1 = Q2 = 4 кН, = 60 , F1 Bу, СЕ Ву, F2 Ву.

Определить реакции связей.

Решение.

Рассматривается равновесие жесткой конструкции АВDD1В1А1. Кон-

струкция нагружена силами F1 ,F2 ,Q1 ,Q2 . На конструкцию наложены связи: в

точке А цилиндрический шарнир – реакции X A ,YA , в точке В сферический

шарнир – реакции X B ,YB ,ZB , в точке С стержневая связь – реакция RC на-

правлена по стержню (рисунок 5.5).

На конструкцию действует произвольная пространственная система сил. Составляется шесть уравнений равновесия. Неизвестных величин тоже шесть, т.е. задача статически определимая

n

X k

0,

X A

X B

F1

cos

RC

cos

0,

k

1

n

Yk

0,

YB

F2

0,

k

1

n

Zk

0,

Z A

ZB

RC

sin

Q1

Q2

F1

sin

0,

k

1

n

mх ( Fk

)

0,

F2 a + Q1 0,5a – RC sin

0,5a – ZA a – F1 sin ·a = 0,

k

1

n

mу ( Fk

)

0,

− RC sin

0,5a − F1 sin

a + Q1 0,5a + Q2 0,5a = 0,

k

1

n

mz ( Fk

)

0,

XA a – F1 cos

a – RC cos

0,5a + F2 a = 0.

k

1

Из второго уравнения определяется YB = F2 = 2 кН.

Из пятого уравнения определяется RC:

RC

Q1 0,5

Q2 0,5 F1

sin

0,5 4

0,5 4

2 0,866

5, 238 кН.

0,5 sin

0,5 0,866

Из четвертого уравнения определяется ZA:

ZA = F2 + Q1 0,5 – RC 0,5sin

− F1sin

=

= 2 + 4 0,5 –5,238 0,5·0,866−2 0,866 = 0.

Из шестого уравнения определяется ХА:

ХА = F1 cos

+ RC 0,5 cos – F2 = 2 0,5 + 5,238 0,5 0,5 – 2 = 0,31 кН.

Из третьего уравнения определяется ZB:

ZB = ZA + RC sin – Q1 – Q2 + F1 sin

=

129

	= 0,536 + 5,238 0,866 – 4– 4 + 2 0,866 = − 1,732 кН.
			z			z
		Е
					RC
						Z B
				Z A
А			В	y		В	YB	y
				А
F	С		a	F1	X B
1				X A		a
					С

А1

В1

y1

Q1

D

А1

Q1

В

1

D

х

х

Q2

F2

D1

Q2

F2

D1

Рисунок 5.4

Рисунок 5.5

Из первого уравнения определяется ХВ:

ХВ = F1 cos + RC cos – XA = 2 0,5 + 5,238 0,5 – 0,31 = 3,309 кН.

Можно составить несколько проверочных уравнений, т.е. записать суммы моментов всех сил относительно других осей.

Например, запишем сумму моментов относительно оси B1y1

n
	my ( Fk ) 0 , − Q1 0,5·a − Q2 0,5·a − ZB a + RC sin 0,5·a + ZA a =
k	1	1
		= − 4 0,5 − 4·0,5 − (−1,732) + 5,238 0,5 0,866 = 0, 0			0.
	Ответ: ХА = 0,31 кН, ХВ = 3,309 кН, ZA = 0, YB = 2 кН,				ZB = − 1,732 кН,
				RC = 5,238 кН.

Знак минус составляющей ZB означает, что еѐ реальное направление будет противоположным показанному на рисунке 5.5.

Пример 2. На барабан простейшей подъемной машины намотан канат на конце которого закреплен груз D, весом Р = 16 кН. К шкиву К, ременной передачи, приложена пара сил с моментом М, удерживающая вал АВ в равновесии. Определить реакции подшипников А и В и натяжения Т1 и Т2 ветвей ремня (Т1 = 2 Т2), R = 0,3 м, r = 0,15 м, = 30 . Вес вала со шкивом и барабаном Q = 6 кН (рисунок 5.6).

Дано: Р = 16 кН, М, Т1 = 2 Т2, R = 0,3 м, r = 0,15 м, = 30 , Q = 6 кН.

Определить реакции подшипников А и В и натяжения Т1 и Т2 ветвей

ремня.

130