Министерство образования и науки Российской Федерации Федеральное государственное автономное образовательное учреждение высшего профессионального образования «Российский государственный профессионально-педагогический университет»

Машиностроительный институт

Кафедра высшей математики

Методические указания для выполнения контрольной работы

по дисциплине

«Математическое программирование»

(ГОС-2000)

для студентов всех форм обучения

специальности 080101.65 Экономическая теория (060100)

Екатеринбург

2012

Методические указания для выполнения контрольной работы по дисциплине «Математическое программирование». Екатеринбург, ФГАОУ ВПО «Российский государственный профессионально-педагогический университет», 2012. 27 с.

Составители: канд. физ.-мат. наук, доцент А.С. Просвиров,

канд. физ.-мат. наук, доцент А.В. Шитиков

Одобрены на заседании кафедры высшей математики Машиностроительного института РГППУ. Протокол от 28 февраля 2012 г. № 7.

Заведующий кафедрой высшей математики Е.А. Перминов

Рекомендованы к печати методической комиссией Машиностроительного института РГППУ. Протокол от 14 марта 2012 г. № 7.

Председатель методической

комиссии МаИ А.В. Песков

© ФГАОУ ВПО «Российский государственный профессионально-педагогический университет», 2012

© Просвиров А.С., Шитиков А.В.

Введение

Математическое программирование (МП) представляет собой математическую дисциплину, занимающуюся изучением экстремальных задач и разработкой методов их решения. В общем виде математическая постановка экстремальной задачи состоит в определении наибольшего или наименьшего значения целевой функции f (х₁, х₂, … х_п) при ограничениях

где f, q_i, q_j – заданные функции; b_i ,b_j- некоторые действительные числа.

Задачи МП делятся на задачи линейного (Л.П.) и нелинейного программирования. Если все функции f и q_i линейные, то соответствующая задача является задачей Л.П. Если же хотя бы одна из них нелинейная, то данная задача – задача нелинейного программирования. Наиболее изученным разделом МП являются задачи Л.П. Среди задач нелинейного программирования наиболее глубоко изучены задачи выпуклого программирования.

Курс МП предусматривает знакомство с основными задачами МП и методами их решения.

§ 1. Экстремум функции одной переменной

Этот материал изучался в курсе математического анализа [1 ]. Здесь мы напомним лишь некоторые основные положения.

Определение 1.1. Точка х₀ называется точкой локального максимума (минимума) функции ƒ(х), если для любого х≠х₀ в некоторой окрестности точки x₀ выполняется неравенство ƒ₍х₎< ƒ(x₀) (ƒ₍х₎> ƒ(x₀).

Теорема 1.1. ( Необходимое условие существования локального экстремума).

Если х₀ - точка локального экстремума функции ƒ₍х₎, то производная ƒ^'(x₀)=0 или ƒ^'(x₀) не существует.

Определение 1.2. Точка x₀ из области определения функции ƒ(х), называется критической точкой, если в ней производная равна нулю (ƒ'(x₀)=0) или не существует.

По теореме 1.1. экстремум может достигаться только в критической точке. Но критическая точка вовсе не обязательно является точкой экстремума.

Достаточные условия существования локального экстремума дают следующие теоремы.

Теорема 1.2. (Первый достаточный признак). Пусть функция ƒ(х) дифференцируема в некоторой окрестности (х₀ – σ, х₀ + σ ) критической точки х₀ , за исключением, быть может, самой этой точки. Тогда, если при переходе через точку х₀ слева направо производная ƒ'(х) меняет знак с плюса на минус, то х₀ – точка локального максимума, а если с минуса на плюс, то х₀ - точка локального минимума.

Теорема 1.3. (Второй достаточный признак). Пусть функция ƒ(х) дважды дифференцируема в критической точке х₀ и в некоторой ее окрестности. Если ƒ^″(x₀)<0, то х₀ - точка локального максимума функции ƒ(х). Если ƒ^″(x)>0, то х₀ – точка локального минимума. Если же ƒ^″(x₀)=0, то требуется дополнительное исследование.

Замечание 1.1. Наличие локального максимума или минимума в некоторой точке промежутка Х вовсе не гарантирует, что в этой точке функция f(x) принимает наибольшее (наименьшее) значение на этом промежутке (или, как говорят, имеет глобальный максимум (минимум)). Но если внутри промежутка X непрерывная функция f(x) имеет единственную точку локального экстремума, то она будет и точкой одноименного глобального экстремума функции на этом промежутке.

Схема исследования функции у = f(x) на локальные экстремумы.

1. Найти область определения функции f(x).

2. Найти производную у^'= f ^' (x).

3. Найти критические точки функции.

4. Исследовать знаки производной в ее области определения (или на заданном промежутке). Для этого рекомендуется использовать известный из школы метод интервалов.

5. Сделать вывод о наличии точек максимумов и минимумов. Найти значения функции в этих точках.

Задание 1. Найти экстремумы функции у = .

1. Так как дискриминант ( квадратного трехчлена в знаменателе отрицателен, то знаменатель нигде не обращается в ноль. Поэтому у_(х) определена и непрерывна на всей числовой оси. ().

2. Найдем производную

у' =[(12-8х+4х²)^-1]' = (–12-8х+4х²)^-2(–8+8х)= .

3. Данная функция имеет только одну критическую точку х_о=1. Точек, где производная не существует, нет (знаменатель положителен при любых х(-R)).

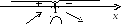4. Знакиf ^'(х):

Поведение f(x):

Экстремумы:

5. Так как при переходе через точку х_о=1 производная меняет знак с "+" на "–", то х_о=1– точка локального максимума. Так как это единственная точка локального экстремума, то в этой точке достигается не только локальный, но и глобальный максимум (наибольшее значение) на всей числовой оси.