§ 3 Условный экстремум. Метод множителей лагранжа

Определение 3.1. Функция ƒ(P)=ƒ(x₁,…,x_n) имеет условный максимум (условный минимум) в точке P₀ (х₁º,…, хº_n), если существует такая окрестность точки P₀, для всех точек P которой (Р ≠ P₀), удовлетворяющих уравнениям связи

φ_κ(Р)=φ_κ(х₁,…,х_п)= 0, κ= 1,2,..,m; m<n

выполняется неравенство ƒ (Р_о) >ƒ (P) ( соответственно ƒ (Р_о) <ƒ (P)).

Задача нахождения условного экстремума сводится к исследованию на обычный экстремум функции Лангранжа

L φ_κ (x_1,…,х_п),

где λ_κ (k=1,2,…,m) называются множителями Лангранжа. Необходимые условия условного экстремума выражаются системой (n + m) уравнений

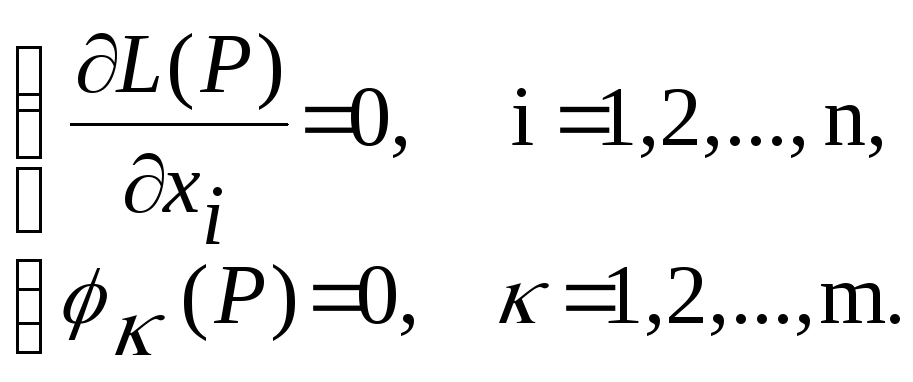
Решая эту систему, получим некоторые наборы чисел

х₁,…, х_n, λ₁,…,λ_m, где х₁,…х_n – координаты точки, в которой возможен условный экстремум.

В частном случае функции z = ƒ (x, у) от двух переменных при одном уравнении связи φ (х,у) = 0 функция Лангранжа имеет вид

L (х,у,λ) = ƒ (х,у) + λ·φ (х,у).

Система состоит из трех уравнений:

φ (х,у)=0.

Пусть Ρ₀(х₀,у₀), λ₀– любое из решений этой системы. Здесь достаточное условие существования в точке Р₀ условного экстремума можно сформулировать так. Обозначим ∆ (L) определитель

.

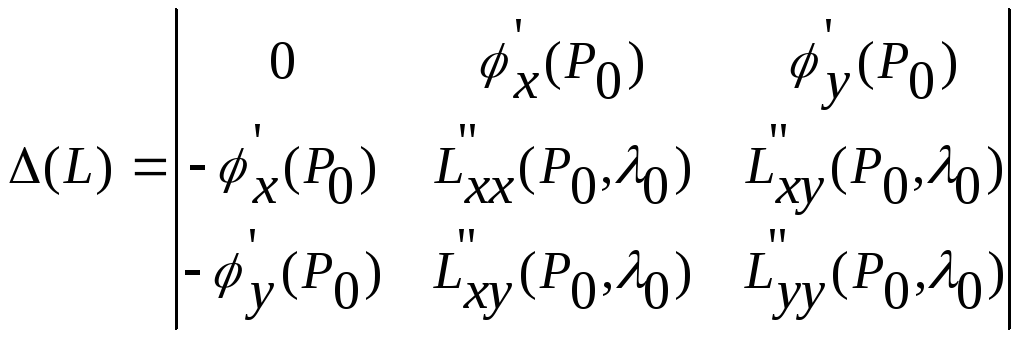Тогда: если ∆<0, то функция z=ƒ(х,у) имеет в точке Р₀(х₀,у₀) условный максимум; если ∆>0 – то условный минимум.

Задача 3.1. На развитие двух предприятий, входящих в производственное объединение., выделено 2 млн.руб. Если первому предприятию дадут х₁ млн.руб., то прибыль, полученная от этого предприятия будет равна 2млн. руб; если х₂ млн.руб. дадут второму, то прибыль от него будет равна 6млн.руб.

Как следует распределить средства между предприятиями, чтобы суммарная прибыль была максимальной? Решить задачу методом множителей Лагранжа.

Р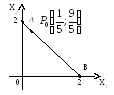ешение.

Задача состоит в отыскивании точки глобального максимума функции

у=2+6при ограничении: х₁+х₂=2,

Множество допустимых решений задачи является отрезок [A, B] (cм. рис.3.1)

Точку возможного максимума найдем методом множителей Лагранжа. Функция Лагранжа имеет вид:

L(х₁,х₂,λ)= 2

Для отыскания точек возможных экстремумов составим систему

Найдем ее решения. Из уравнений (1) и (2) получаем

–.

Подставляя найденное соотношение x₂=9x₁ в уравнение (3), получим x₁+9x₁–2=0, откуда x_{1 =} , а поэтому x₂ = 9x₁ =, наконец .

Итак, система имеет одно решение

Исследуем найденную точку на локальный условный экстремум с помощью определителя

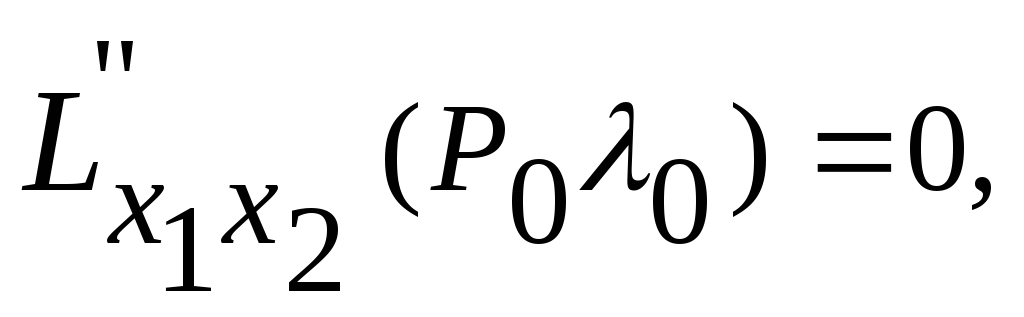
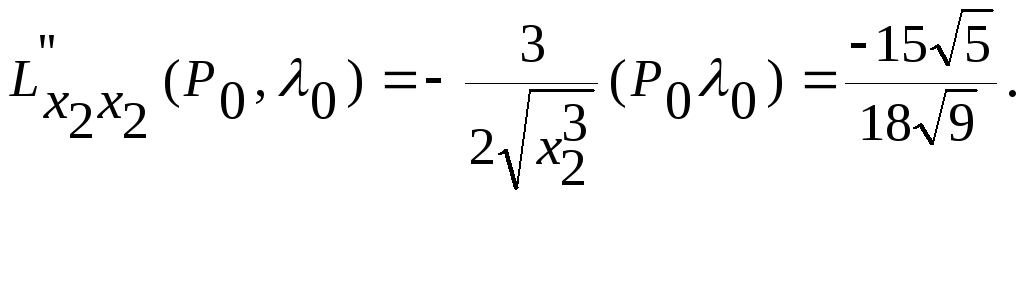
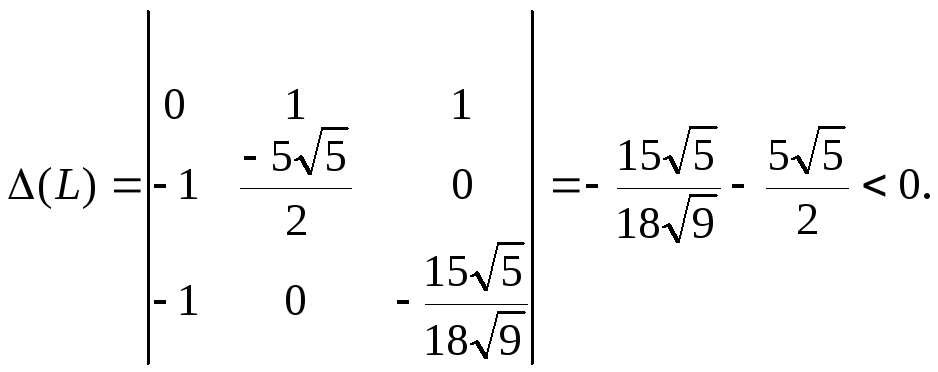
Так как – то – точка локального условного максимума.

Чтобы показать, что в этой же точке достигается и глобальный максимум, перейдем к задаче на отыскание безусловного максимума функции одной переменной. С помощью условия связи x₁+x₂=2 запишем целевую функцию в виде

. Требуется найти точку, где достигается наибольшее значение (глобальный максимум) функции одной переменной f(x₁). Область возможного изменения оставшейся переменной – отрезок . Как известно из математического анализа, непрерывная функция на замкнутом отрезке обязательно достигает своего наибольшего и наименьшего значений либо в критических точках внутри отрезка, либо на его границах.

Ищем критические точки внутри отрезка

. Из условия f '(x₁)=0 находим стационарную точку:== х₁= 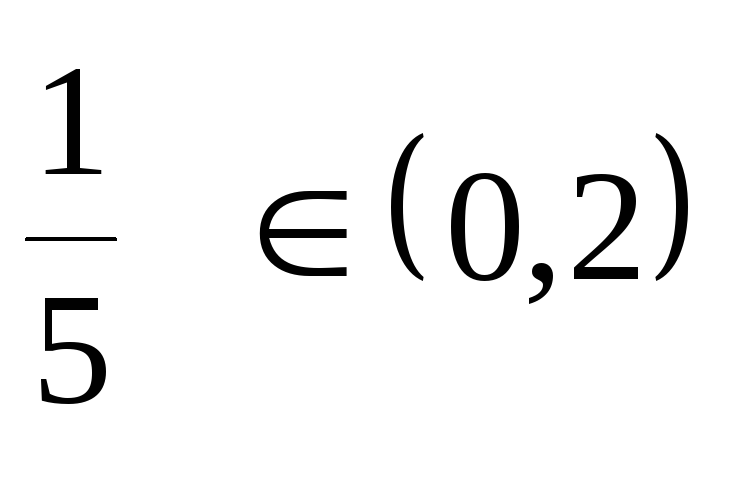. Точек, где производная не существует, внутри отрезка нет.

Находим значения целевой функции на границах отрезка и в стационарной точке .

,

Так как > >,то наибольшее значение достигается в точке .

Итак, глобальный максимум достигается при млн. руб., млн. руб. при этом у = 4 млн. руб.