§ 4 Постановка задачи линейного программирования. Графический метод решения.

Общую задачу линейного программирования (ЗЛП) можно записать так:

(4.1)

при ограничениях

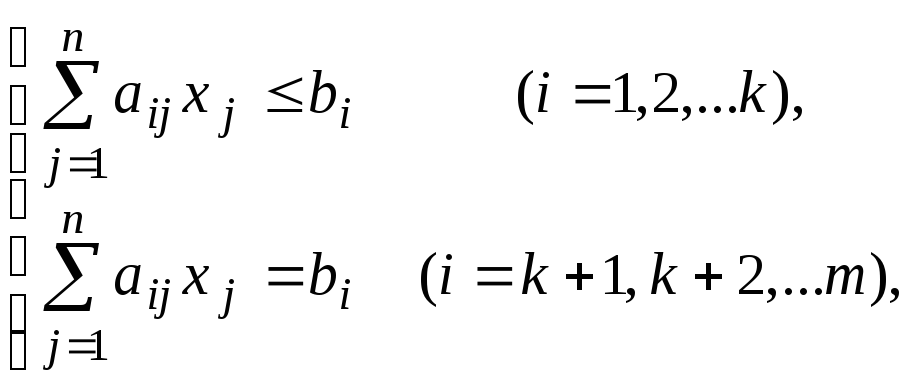(4.2)

x_j ≥ 0 (ј = 1,2,…n ) (4.3)

Здесь линейная функция f (4.1) называется целевой функцией, а (4.2) и (4.3) – системой ограничений. Неотрицательное решение (x₁,x₂,…x_n) системы (4.2) называется допустимым решением (планом) ЗЛП. Допустимое решение, при котором целевая функция f принимает максимальное (или минимальное) значение, называется оптимальным решением. Требуется найти оптимальное решение ЗЛП.

Если в систему ограничений (4.2) входят только неравенства, то ЗЛП называется стандартной (или симметричной), если же система ограничений (4.2) состоит из одних уравнений, то ЗЛП называется канонической (или основной). Любая ЗЛП может быть записана как в стандартной, так и в канонической форме. Например, с помощью введения дополнительной (балансовой) переменной x₃ ≥ 0 неравенство a₁₁х₁ + α₁₂ x₂ ≤ b₁ можно заменить уравнением α₁₁х₁ + α₁₂ x₂+x₃ = b₁, а неравенству α₁₁х₁ + α₁₂ x₂ ≥ b₁соответствует уравнение α₁₁х₁ + α₁₂ x₂ – х₃ = b₁

Задачу минимизации целевой функции часто бывает целесообразно свести к задаче максимизации. Делается это так: если требуется найти минимум функции f = c₁ x₁+…c_n x_n, то это будет равносильно отысканию максимума функции f₁= –f =

–c₁x₁–…–c_n x_n с последующей заменой знака на противоположный у найденного значения max f, поскольку min f = –max (-f).

Геометрическая интерпретация злп.

Рассмотрим задачу Л.П с двумя переменными f = c₁ x₁+c₂ x₂→ max (min), при ограничениях

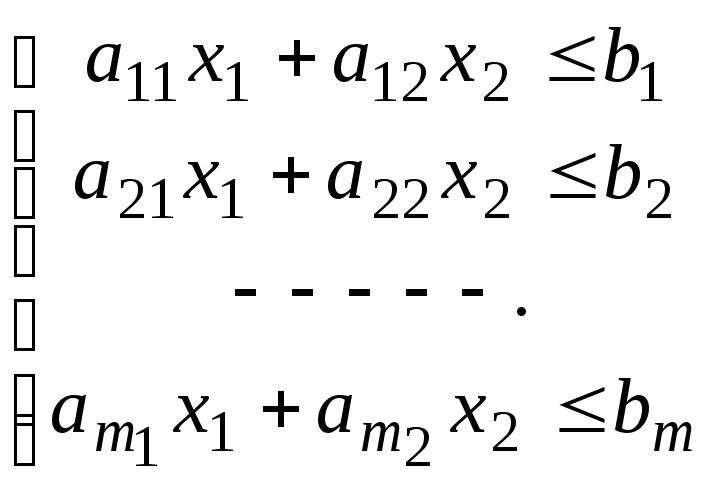(4.4)

Система ограничений (4.4) геометрически представляет собой выпуклый многоугольник (или выпуклую многоугольную область) как пересечение полуплоскостей – геометрических образов неравенств системы. Множество точек постоянного значения целевой функции f = c₁x₁+ c₂x₂=h (h=const) – прямая, перпендикулярная вектору При перемещении этой прямой в направлении вектора значение h целевой функции в точках прямой растет, в противоположном направлении – убывает. На этих утверждениях основан графический метод решения ЗЛП.

Алгоритм графического методы решения ЗЛП.

1). В системе координат построить прямые по уравнениям, соответствующим каждому неравенству системы (4.4).

2). Найти полуплоскости решения каждого неравенства системы, ограниченные построенными прямыми (обозначить стрелками).

3). Найти многоугольник (многоугольную область) решений системы ограничений как пересечение полуплоскостей .

4). Построить вектор по коэффициентам целевой функции

f = c₁x₁+ c₂x_2.

5). Перпендикулярно вектору провести одну из прямых постоянного значения целевой функции, например, проходящую через начало координат.

6). Перемещая эту прямую параллельно самой себе в направлении вектора

,, найти точку входа (в ней достигается min f) в многоугольник допустимых решений и точку выхода (max f) из многоугольника.

7). Найти координаты точки входа (если решается задача на минимум ) или точки выхода (при решении задачи на максимум) и вычислить значение f в найденной точке.

Замечание. В случае, если одно из ребер многоугольника допустимых решений ортогонально вектору , то во всех точках этого ребра достигается максимальное (или минимальное) значение целевой функции, т.е. ЗЛП может иметь бесконечное множество решений. Если же область допустимых решений не ограничена, то ЗЛП может не иметь решения.

Задача 4.1. Решить графическим методом.

Для изготовления двух видов продукции Р₁ и Р₂ используют четыре вида ресурсов S₁, S₂, S₃ и S_4.. Запасы ресурсов, затрачиваемых на изготовление единицы продукции, приведены в таблице (цифры условные).

Таблица 4.1

Вид ресурса	Запас ресурса (усл. ед.)	Число единиц ресурсов, затрачиваемых на изготовление единицы продукции
		Р1	Р2
S1	18	1	3
S2	16	2	1
S3	5	–	1
S4	21	3	–

Прибыль, получаемая от единицы продукции Р₁ и Р₂ – соответственно 2 и 3 руб.

Нужно составить такой план производства продукции, при котором прибыль от ее реализации будет максимальной.

Покажем, что этот пример является задачей линейного программирования. Обозначим x_1,x₂ – количество единиц продукции соответственно Р₁ и Р₂ , запланированных к производству.

Для изготовления (см. табл. 4.1) потребуется (1·x₁+ 3x₂) единиц ресурса S₁, (2x₁+ 1·x₂) единиц ресурса S₂ , (1·x₂) единиц ресурса S₃ и 3x₁ единиц ресурса S₄. Так как потребление ресурсов S₁, S₂, S₃, S₄ не должно превышать их запасов, соответственно 18,16,5 и 21 единиц, то связь между потреблением ресурсов и их запасами выражается системой неравенств:

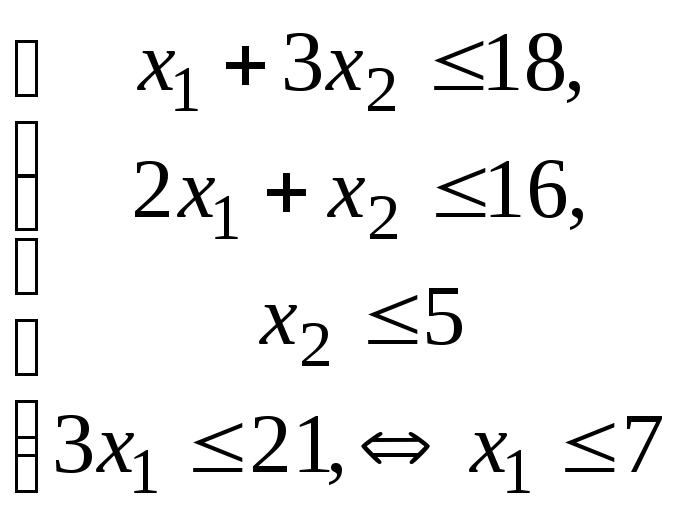(4.5)

Далее, по смыслу задачи

. (4.6)

Суммарная прибыль f cоставит 2х₁ руб. от реализации продукции Р₁ и 3х₂ руб. – от реализации продукции Р₂, т.е.

ƒ(x₁,x₂)=2x₁+3х₂→max. (4.7)

Таким образом, получили математическую модель задачи: найти план выпуска продукции Х = (х₁,х₂), удовлетворяющий системам линейных неравенств (4.5), (4.6), при котором линейная целевая функция (4.7) принимает максимальное значение, т.е. данная задача является задачей ЛП.