
- •Методические указания для выполнения контрольной работы
- •«Математическое программирование»
- •Введение
- •§ 1. Экстремум функции одной переменной
- •§ 2 Локальные и глобальные экстремумы функции нескольких переменных.
- •§ 3 Условный экстремум. Метод множителей лагранжа
- •§ 4 Постановка задачи линейного программирования. Графический метод решения.
- •Геометрическая интерпретация злп.
- •Графический метод решения.
- •§ 5 Симплекс-метод решения задач линейного программирования
- •§ 6 Транспортная задача
- •Литература
- •Методические указания для контрольной работы
§ 2 Локальные и глобальные экстремумы функции нескольких переменных.
При изложении этого материала предполагается знание студентами раздела курса математического анализа, касающегося функций нескольких переменных, а также сведений из курса линейной алгебры (матрицы и определители). Напомним некоторые определения и теоремы.
Определение 2.1. Всякий упорядоченный набор n действительных чисел называется точкой п-мерного арифметического пространства Rn, а сами числа х1, х2, … хn называются координатами этой точки Р=Р(х1,х2 … хn).
Определение
2.2. Пусть
![]() – произвольное множество точек n-мерного
арифметического пространства. Если
каждой точке Р(х1,
х2
…хn)
– произвольное множество точек n-мерного
арифметического пространства. Если
каждой точке Р(х1,
х2
…хn)![]() поставлено в соответствие действительное
число f
(Р)=f
(x1,
x2…xn),
то говорят, что, на множестве D
задана
числовая функция
f
от n
переменных. Множество D
называется областью определения функции
f(Р).
поставлено в соответствие действительное
число f
(Р)=f
(x1,
x2…xn),
то говорят, что, на множестве D
задана
числовая функция
f
от n
переменных. Множество D
называется областью определения функции
f(Р).
Определение
2.3. Пусть
P(x,
у) произвольная
точка из области определения функции
двух переменных Z
= f(x,у).
Предел
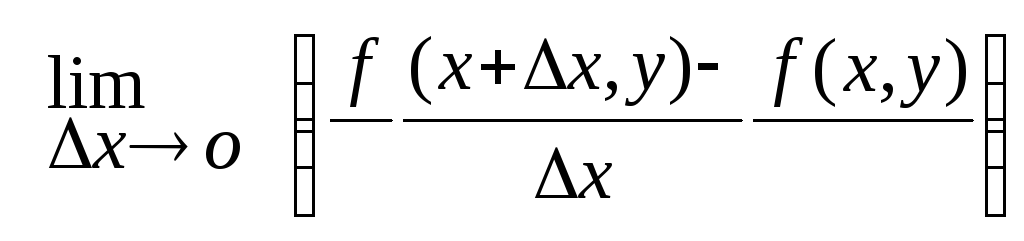 называется частной производной данной
функции по переменной х
в точке P(x,
у) и обозначается
называется частной производной данной
функции по переменной х
в точке P(x,
у) и обозначается
![]()
![]() или Zx',
или f
'
, или
или Zx',
или f
'
, или![]() .
.
Аналогично
Z′у
=![]() =
=![]() .
.
![]()
![]() называется
частной производной по у
в точке P(x,
у).
называется
частной производной по у
в точке P(x,
у).
Для функций с большим числом переменных понятие частных производных вводится аналогично.
Из этих определений следует, что вычисление частной производной функции нескольких переменных производится так же, как и для функции одной переменной. При этом все переменные, кроме той, по которой производится дифференцирование, считаются константами.
Определение 2.4. Частными производными второго порядка функции
Z = f(x,у) называются частные производные от ее частных производных первого порядка и обозначаются так
![]()
![]()
![]()
Смешанные
производные
![]() и
и
![]() ,
равны между
собой, если они непрерывны (что обычно
выполняется).
,
равны между
собой, если они непрерывны (что обычно
выполняется).
Определение 2.5. Точка Р0 называется точкой локального минимума (максимума) функции ƒ(Р), если для любой точки P ≠Po из некоторой окрестности точки Р0 выполняется неравенство ∆ ƒ(Pо)= ƒ(P)– ƒ(Pо)>0(∆ ƒ(Pо)<0).
Теорема 2.1. (необходимое условие экстремума).
Если дифференцируемая функция ƒ(P) достигает экстремума в точке
P0=Р
(x1º,x2º…xnº),
то в этой
точке
![]() для всех i
=1,2,…n.
для всех i
=1,2,…n.
Точки,
где все![]() =0
называется стационарными. Таким образом,
экстремум может достигаться либо в
стационарных точках, либо в таких, где
ƒ(P)
недифференцируема.
=0
называется стационарными. Таким образом,
экстремум может достигаться либо в
стационарных точках, либо в таких, где
ƒ(P)
недифференцируема.
Для решения вопроса о том, является ли стационарная точка P0 точкой экстремума, нужно рассмотреть знак приращения функции в этой точке.
∆ƒ(Ро)=ƒ(Р)–
ƒ(Ро)
≈ d ƒ(Ро)+
![]() d²
ƒ(Ро)
d²
ƒ(Ро)
Последнее равенство выполняется тем точнее, чем меньше приращения независимых переменных ∆ xi ≡ dxi = xi–xºi.
Здесь d ƒ(Ро) – первый дифференциал функции ƒ(Р) в точке Р0.
d
ƒ(Ро)=
![]() .
В стационарной
точке d ƒ(Pо)
= 0.
.
В стационарной
точке d ƒ(Pо)
= 0.
d2
ƒ(Ро)
=
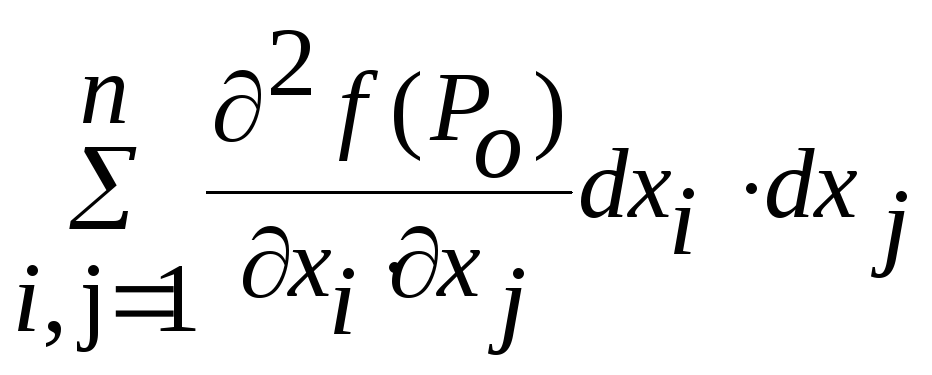
второй дифференциал функции ƒ(Р) в этой точке.
Теорема 2.2. (Достаточное условие экстремума).
Пусть P0 стационарная точка функции ƒ(Р), причем эта функция дважды дифференцируема в некоторой окрестности точки Р0 и все ее вторые частные производные непрерывны в этой точке. Тогда:
1) если второй дифференциал d² ƒ(Ро)>0 (d² ƒ(Ро)<0) для любых наборов dхi (не равных нулю одновременно), то Р0 – точка локального минимума (максимума). В этом случае матрица, составленная из вторых производных функции
f
(x1,
x2…xn)
в этой точке – матрица Гессе Hf
=
![]()
называется положительно (отрицательно) определенной;
2) если d² ƒ(Ро)>0 для одних наборов dxi и d² ƒ(Ро) )<0 для других наборов dxi , то в P0 нет экстремума. Матрица Гессе называется неопределенной.
3) если d² ƒ(Ро)>0 для одних наборов dxi и d² ƒ=0 для других наборов dxi (но dxi ≠ 0 одновременно), то матрица Гессе называется положительно полуопределенной. Аналогично, если d² ƒ≤ 0 то Hf, называется отрицательно полуопределенной. И в том и другом случае для решения вопроса о существования локального экстремума в точке Ро требуется дополнительное исследование.
Теорема 2.3. (Критерий Сильвестра). Для того, чтобы матрица Гессе
Hf (Ро) была положительно определена, необходимо и достаточно, чтобы все n ее угловые миноры были положительны, то есть
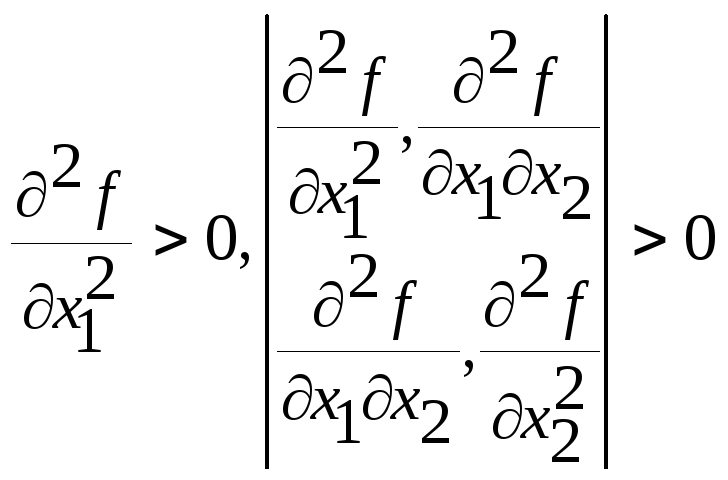 …
и т.д.
…
и т.д.
В
случае отрицательной определенности
матрицы Hf
знаки ее
угловых миноров чередуются, начиная со
знака "минус" для минора I-го
порядка:
![]() .
.
Определение 2.6. Главным минором квадратной матрицы А называется определитель любой матрицы, полученной из А вычеркиванием части ее строк и столбцов с одинаковыми номерами. Всего главных миноров для матрицы n-ого порядка будет (2n–1)штук.
Теорема 2.4. (Критерий Сильвестра). Для того, чтобы матрица Гессе была положительно полуопределена, необходимо и достаточно, чтобы все ее главные миноры были неотрицательны (но хотя бы один из угловых миноров должен быть равен нулю). Для того, чтобы матрица Гессе Hf была отрицательно полуопределена в точке Р, необходимо и достаточно, чтобы (–Hf) была положительно полуопределена.
В частном случае функции двух переменных достаточные условия экстремума можно сформулировать следующим образом.
Теорема 2.5. Пусть Рo (xo, уо) стационарная точка функции z = f(x,у), причем эта функция дважды дифференцируема в некоторой окрестности точки Рo и все ее частные производные второго порядка непрерывны в Рo.
Введем обозначения:
A=
![]() B=
B=![]() C=
C=
![]() ,
,![]() .
.
Тогда:
1)если D>0, A>0 – Pо – точка минимума,
D>0, A<0 – Pо – точка максимума,
2) если D < 0 – экстремума в точке Pо нет;
3) если D = 0, то требуется дополнительное исследование.
В приложениях (в частности, экономических) наибольший интерес представляют не локальные, а глобальные экстремумы функции.
Определение
2.7. Пусть
функция f
(Р)=f
(x1,x2…xn)
определена на множество![]() Rn.
Говорят, что в точке
Rn.
Говорят, что в точке![]() функция f
достигает глобального
минимума
(принимает наименьшее значение) на
множестве Х,
если для
всех точек
функция f
достигает глобального
минимума
(принимает наименьшее значение) на
множестве Х,
если для
всех точек![]() выполняется неравенство
выполняется неравенство![]() аналогично, f
достигает
глобального максимума
(принимает наибольшее значение) на
множестве Х,
если для всех точек
аналогично, f
достигает
глобального максимума
(принимает наибольшее значение) на
множестве Х,
если для всех точек![]() имеет место
имеет место
![]()
![]()
Задача отыскания наибольшего и наименьшего значений непрерывной функции на замкнутом множестве в случае функций одной и двух переменных рассматривалась в курсе математического анализа [ 1 ].
Особый интерес представляют выпуклые (и вогнутые) функции. Оказывается, что для них локальный экстремум является и глобальным.
Определение 2.8. Множество называется выпуклым, если вместе с любыми двумя своими точками оно полностью содержит и отрезок, их соединяющий.
С ледующие
рисунки иллюстрируют различие между
выпуклым и не выпуклым множеством точек
плоскости. Рис. 2.2.
ледующие
рисунки иллюстрируют различие между
выпуклым и не выпуклым множеством точек
плоскости. Рис. 2.2.
Определение
2.9. Функция
f(Р), определенная
на выпуклом множестве
![]() Rn
называется выпуклой (вогнутой), если
любой отрезок [AB],
соединяющий
две точки ее графика лежит " не ниже"
(" не выше") соответствующих точек
графика.
Rn
называется выпуклой (вогнутой), если
любой отрезок [AB],
соединяющий
две точки ее графика лежит " не ниже"
(" не выше") соответствующих точек
графика.
Иллюстрация для случая функции одной переменной представлена на следующем рис.2.3.
Т еорема
2.6. Пусть
f(Р) дважды
непрерывно дифференцируема на открытом
выпуклом множестве
еорема
2.6. Пусть
f(Р) дважды
непрерывно дифференцируема на открытом
выпуклом множестве![]() Rn.
Тогда для выпуклости f
на Х
необходимо и достаточно, чтобы ее матрица
Гессе была положительно или полуположительно
определена в каждой точке
Rn.
Тогда для выпуклости f
на Х
необходимо и достаточно, чтобы ее матрица
Гессе была положительно или полуположительно
определена в каждой точке
![]() .
.
Для доказательства вогнутости f(Р) достаточно доказать выпуклость функции (– f(Р)).
Задача 2.1. Найти минимум функции у=(х1–7)2 + (х2–6)4. Является ли данная функция выпуклой?
Решение. Найдем частные производные 1-го порядка и составим систему уравнений
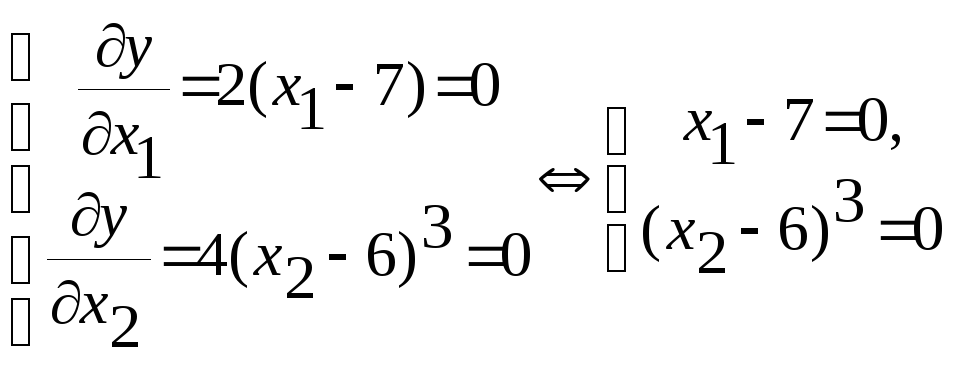
Решая ее, найдем критическую (стационарную) точку Р0 (7,6). Найдем далее частные производные 2-го порядка:
![]() Найдем
значение D=АС-В2
в стационарной точке Р0.
А =
Найдем
значение D=АС-В2
в стационарной точке Р0.
А =
![]()
D=
АС–В2=2·0–0²=0.
Согласно п. 3 теоремы 2.5, требуется
дополнительное исследование. Для этого
найдем полное приращение функции у
(х1,х2)
в стационарной точке
![]() ∆у (Р0)
= ∆у (7,6)=(7+∆ х1–7)2
+ (6+∆ х2-6)4
– ((7-7)2
+ (6-6)4)=∆
х1²
+ ∆х24>0
для любых ∆х1,
∆х2
не равных одновременно нулю. Следовательно,
Р0 (7,6)
– точка локального минимума, Уmin
= 0
∆у (Р0)
= ∆у (7,6)=(7+∆ х1–7)2
+ (6+∆ х2-6)4
– ((7-7)2
+ (6-6)4)=∆
х1²
+ ∆х24>0
для любых ∆х1,
∆х2
не равных одновременно нулю. Следовательно,
Р0 (7,6)
– точка локального минимума, Уmin
= 0
![]()
Проверим функцию на выпуклость. Прежде всего, отметим, что функция у определена на всей координатной плоскости R2 (открытом выпуклом множестве). Ее матрица Гессе в произвольной точке (х1,х2) имеет вид
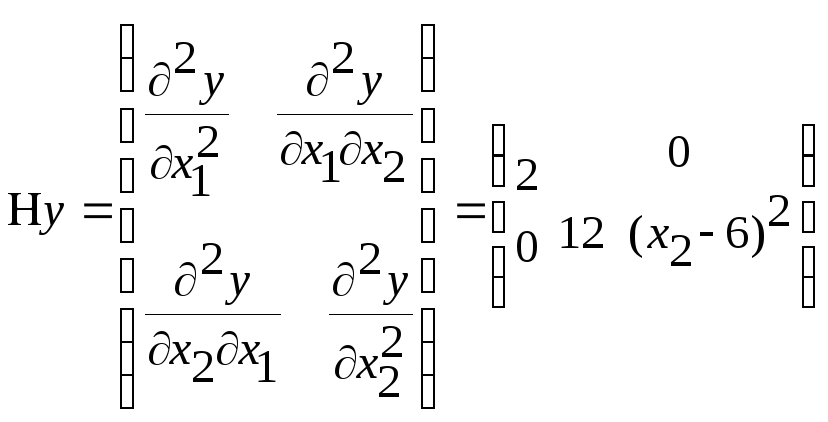 .
.
Матрица
Hу
положительно полуопределена, поскольку
знаки всех ее главных миноров в любой
точке (х1,х2)
![]() R2
неотрицательны: ∆1=2>0,
∆2
=12 (х2—6)2 ≥0,
∆3
=
R2
неотрицательны: ∆1=2>0,
∆2
=12 (х2—6)2 ≥0,
∆3
=
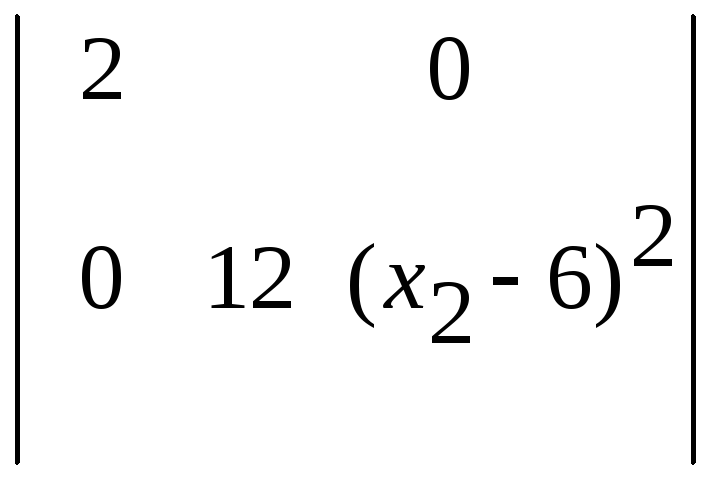 = 24 (х2—6)2
≥ 0.
= 24 (х2—6)2
≥ 0.
Следовательно, функция у будет выпуклой на всем пространстве R2,а потому в точке Р0 (7,6) она достигает глобального минимума.
Задача
2.2. Найти
минимум функции у=(х1–х2)2
+х![]() .
Является ли данная функция выпуклой?
.
Является ли данная функция выпуклой?
Решение. Найдем частные производные 1-го порядка и составим систему уравнений
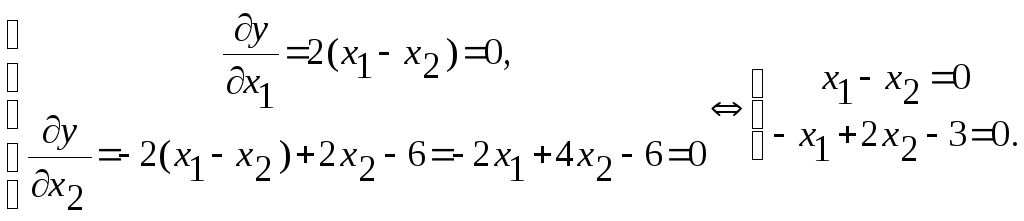
Решая ее, найдем критическую (стационарную) точку Р0 (3,3). Найдем далее частные производные 2-го порядка:
![]()
D = АС–В2=2∙4–(–2)²=4 .
Так как D>0 и А > 0, то Р0 (3,3) – точка локального минимума:
У
min
= (х1–х2)2
+ х![]() –6х2
–6х2
![]()
Проверим
функцию на выпуклость. Прежде всего,
отметим, что функция у
определена на всей координатной плоскости
R2
(открытом выпуклом множестве). Ее матрица
Гессе в любой точке (х1
х2)![]() имеет один и тот же вид.
имеет один и тот же вид.
Ну
=

Матрица
Ну
положительно определена на координатной
плоскости R2,
так как ее угловые миноры положительны:![]()
![]() Следовательно, функция у
будет
выпуклой на всем пространстве R2,
а потому в точке Р0
(3,3) она достигает глобального минимума.
Следовательно, функция у
будет
выпуклой на всем пространстве R2,
а потому в точке Р0
(3,3) она достигает глобального минимума.
