Arkhiv_ZIP_-_WinRAR / Chast_6_FNP

Теорема. Если функция

f ( x, y)

определена в некоторой окрестности точки

( x0 , y0 ) D , в которой существуют непрерывные производные

′

′

,

′′

′′

то

f x ,

f y

f xy ,

f yx ,

смешанные

производные

не

зависят от

порядка дифференцирования,

т.е.

′′

( x0 , y0 ) =

′′

( x0 , y0 ) .

f xy

f yx

ПРИМЕР

z = x y ,

x > 0 .

∂z

= y x y −1 ;

∂x

∂2 z

= yx y −1 ln x + x y −1 ;

∂x∂y

∂z

= x y ln x ;

∂y

∂2 z

= yx y −1 ln x + x y −1 ,

значит

∂ 2 z

=

∂ 2 z

.

∂y∂x

∂x∂y ∂y∂x

ПРИМЕР

z = y ln x .

∂z

y

∂z

∂ 2 z

∂

y

y

∂ 2 z

∂

(ln x) = 0 ,

∂2 z

∂2 z

1

=

;

= ln x ,

=

= −

,

=

=

=

.

2

x 2

∂y 2

∂x x ∂y

∂x

∂x

x

∂y

∂y∂x ∂x∂y x

ПРИМЕР

Вычислим

производную

восьмого

порядка

∂8 z

функции

∂y3∂x5

z = x 2 + x + x3 + 2x 4 + x 7 y 9 + y10 .

Последовательно вычисляем:

∂z

= x 7 9 y 8 + 10 y 9 ;

∂y

∂ 2 z

= 9 8x 7 y 7 + 10 9 y8 ;

∂y 2

∂3 z

= 9 8 7 x7 y 6

+ 10 9 8 y 7 ;

∂y 3

∂4 z

= 9 8 7 7 x6 y6 ;

∂y3∂x

∂5 z

= 9 8 7 7

6x5 y6 ;

∂y3∂x2

∂6 z

= 9 8 7 7

6 5x4 y6 ;

∂y3∂x3

∂7 z

= 9 8 7 7

6 5 4x3 y6 ;

∂y3∂x4

∂8 z

= 9 8 7 7 6 5 4 3x2 y6 =

7 9!

x2 y6 .

∂y3∂x5

2

1.8. Дифференциалы высших порядков

Пусть z = f ( x, y) , ( x, y) D .

11

В предположении о существовании непрерывных частных производных второго порядка вычислим дифференциал d 2 z второго порядка функции z как дифференциал первого порядка от дифференциала функции dz при условии, что

dz	является функцией только x	и y . При вычислении дифференциала от dz			dx
и	dy считаются постоянными,	при вычислении дифференциала от	∂z	и	∂z
			∂x		∂y

приращения x и y берутся равными dx и dy .

	∂z		∂z
d 2 z = d (dz) = d		dx +
	∂x		∂y

		∂z			∂z
dy	= d		dx + d			dy =
		∂x
					∂y

= ∂ ∂z dx +

∂x ∂x

∂		∂z				∂		∂z
			dy dx +
∂y		∂x				∂x		∂y

	∂		∂z
dx +				dy dy =
	∂y		∂y

=

∂ 2 z

dx 2 +

∂ 2 z

dxdy +

∂ 2 z

dy 2 +

∂ 2 z

dydx =

∂x 2

∂x∂y

∂y 2

∂y∂x

=

∂ 2 z

dx 2 + 2

∂ 2 z

dxdy +

∂ 2 z

dy 2

, где dx 2

= (dx) 2

, dy 2 = (dy)2 .

∂x 2

∂x∂y

∂y 2

Итак,

d 2 z =

∂ 2 z

dx 2 + 2

∂ 2 z

dxdy +

∂ 2 z

dy 2 .

2

2

∂x

∂x∂y

∂y

Использование

символа d =

∂

dx +

∂

dy

позволяет записать

d 2 z как

∂x

∂y

∂

∂

2

результат действия этого оператора на z

в виде:

d

2 z =

dx +

dy

z

.

∂x

∂y

Аналогично: d 3 z = d (d 2 z) = d (d (dz ))

∂

∂

3

=

dx +

dy

z ,

∂x

∂y

n

n−1

∂

∂

n

d

z =d (d

z)=

dx +

dy z .

∂x

∂y

Сама функция при этом может рассматриваться как дифференциал нулевого порядка, z =d 0 z .

ПРИМЕР

Найдем d 2 z , если z = sin xy .

d 2 z =

∂ 2

z

(dx) 2 + 2

∂ 2 z

dxdy +

∂ 2

z

(dy) 2

,

∂z

= cos xy y ,

∂z

= cos xy x ,

∂x

2

∂y

2

∂x∂y

∂x

∂y

∂ 2 z

= − sin xy y

2

,

∂2 z

= −sinxy x2 ,

∂ 2 z

= − sin xy xy + cos xy ,

∂x 2

∂x∂y

∂y2

d 2 z = − y 2sinxydx2 + 2( cosxy − xysinxy )dxdy − x2sinxydy 2 .

12

1.9. Формула Тейлора

Пусть функция

f (M )= f (x, y) дифференцируема n +1 раз в некоторой

окрестности точки M 0 (x0 , y0 ). Тогда для любой точки

M (x, y) из

этой

окрестности справедлива формула Тейлора:

n

1

f (M )=∑

d k f (M 0 , x, y)+Rn (M1 , x, y)=

k=0

k !

= f (M 0 )+

1

df (M 0 , x, y)+

1

d 2 f (M 0 , x, y)+...

1!

2!

...+

1

d n (M 0 , x, y)+Rn (M1 , x, y).

n!

Здесь x = x −x0 ,

y = y −y0 ,

Rn (М1 , x, y)=

1

d n+1 f (М1 ; x, y) M1

–

точка, лежащая на прямой,

n +1 !

(

)

соединяющей точки M ( x, y ) и M 0 ( x, y ) , а d n z =

∂

x +

∂

n

y z .

∂x

∂y

Если уравнение прямой, соединяющей точки M ( x, y )

и M 0 ( x, y ) ,

задано

параметрически,

то

координаты

точки

M1 ( x1, y1 )

имеют

вид:

x1 = x0 + ( x − x0 )θ, y1 = y0 + ( y − y0 )θ, 0 < θ < 1.

n

1

Сумма однотипных слагаемых ∑

d k f (M

0 , x, y) представляет собой

k=0

k !

многочлен Тейлора

n –го порядка, а

последнее

слагаемое

Rn (M1 , x, y) –

называется остаточным членом в форме Лагранжа. Эта форма часто используется при оценке величины остаточного члена в процессе приближенных вычислений.

Если функция f (M )= f (x, y) дифференцируема n раз в некоторой окрестности точки M 0 (x0 , y0 ), то для любой точки M (x, y) из этой

окрестности справедлива формула Тейлора с остаточным членом в форме Пеано:

Rn (M1 , x, y)=o(ρn ), где ρ=( x − x0 )2 + ( y − y0 )2 . В этой форме записи подчеркивается, что при бесконечно малых x и y остаточный член – бесконечно малая более высокого порядка по сравнению с остальными слагаемыми.

ПРИМЕР

Запишем формулу Тейлора для функции z = e xy в окрестности точки P(1,1)

до членов 1-го порядка включительно:

13

f ( x, y) = f ( x , y

) +

∂f ( x0 , y0 )

( x − x ) +

∂f ( x0 , y0 )

( y − y

) + R

( M , x, y)

0

0

∂x

0

∂y

0

2

1

Вычисляя частные производные f ( x, y ) = e xy

в точке (1,1), получаем:

exy = e +

1

e ( x − 1) + ( y − 1) +

1!

1

e ( x − 1)

2

2

(

)

(

)

+

+ 4( x − 1)( y

− 1) + ( y − 1)

e

2!

или

1

(

).

exy = e +

e

( x −1) + ( y - 1) + o

( x −1)2 + ( y −1)2

1!

1.10. Производная сложной функции

Пусть функции u = u( x, y) ,

υ = υ( x, y) определены в области ( x, y) D , а на

множестве их значений определена функция

z = F (u,υ) . Рассмотрим сложную

функцию z = F [u( x, y),υ ( x, y)] .

Пусть функции F (u,υ) , u( x, y) , υ ( x, y)

в своих областях определения имеют

непрерывные частные производные по всем своим аргументам.

Вычислим

∂z

и

∂z

.

Дадим x

приращение

x

при постоянном

y , тогда u

∂x

∂y

примет значение

u +

x u , а υ примет значение υ +

xυ .

Полное приращение функции z

принимает вид:

z =

∂F

u +

∂F

υ + α

u + β

υ , где α, β – бесконечно малые функции при

x

x

∂u

∂υ

x

x

xu → 0 ,

xυ → 0 .

z

=

∂F

xu

+

∂F

xυ

+ α

xu

+ β

xυ

;

x ∂u x ∂υ

x

x

x

Устремим

x

к

нулю,

при этом

x u → 0 и xυ → 0

в силу непрерывности

u и υ .

Так как

lim

z

=

∂z

,

lim

x u

=

∂u

,

lim

xυ

=

∂υ

,

lim α = lim α= lim β = lim β = 0 ,

x→0

x ∂x

x→0

x

∂x

x→0

x

∂x

xu →0

x→0

x v→0

x→0

то

∂z

=

∂F

∂u

+

∂F

∂υ

.

∂x

∂u

∂x

∂υ

∂x

Аналогично:

∂z

=

∂F

∂u

+

∂F

∂υ

.

∂y

∂u

∂y

∂υ

∂y

ПРИМЕР

z = ln(u 2 + υ ), u = e x+ y 2 , υ = x 2 + y .

Вычислим

∂z

и

∂z

.

∂x

∂y

∂z

=

2u

,

∂z

=

1

;

∂u u 2 + υ ∂υ u 2 + υ

∂u

= e x+ y 2 ,

∂u

= 2 ye x+ y 2 ;

∂x

∂y

14

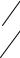
∂υ

= 2x ,

∂υ

= 1 ;

∂x

∂y

∂z

=

2u

e x + y 2 +

1

2 x =

2

(u e x + y 2 + x);

u 2 + υ

∂x u 2 + υ

u 2 + υ

∂z

=

2u

2 ye x+ y 2

+

1

=

1

(4uye x+ y 2

+ 1).

∂y u 2 + υ

u

2 + υ u 2 + υ

Полная производная

Пусть z = F ( x, y) , где y = f ( x) .

dz

=

∂F

∂x

+

∂F

∂y

,

dx

∂x ∂x

∂y ∂x

т.е.

dz

=

∂F

+

∂F

dy

.

dx

∂x ∂y dx

Если z = F ( x, y) , где x = x(t ) ,

y = y(t) , то

dz

=

∂F

dx

+

∂F

dy

.

dt ∂x dt ∂y dt

1.11. Инвариантность формы полного первого дифференциала

Пусть z = F (u,υ) , где u = u( x, y) ,

υ = υ ( x, y) .

′

′

Покажем, что форма первого дифференциала не меняется и dz = zu du + zυ dυ .

Действительно,

+ z′υ ′ )dx + (z

′ )dy =

dz = z′ dx + z′ dy = (z′ u′

′ u′

+ z′υ

x

y

u

x

υ

x

u

y

υ

y

′

′

′

′

′

′

′

′

= zu (ux dx

+ u y dy )+ zυ

(υ x dx +

υ y dy ) = zu

du + zυ dυ .

1.12. Производная от функции, заданной неявно

Уравнение F ( x, y) = 0 неявно задает функцию одной переменной y = y( x) . Теорема. Если F ( x, y) и ее частные производные Fx′( x, y) и Fy′( x, y)

определены

и

непрерывны

в

некоторой области,

содержащей

точку

( x, y) ,

0 и

′

≠ 0 , то

′

Fx′( x, y)

.

F ( x, y) =

= −

Fy ( x, y)

yx

Fy′( x, y)

Доказательство:

Пусть F ( x, y) = 0 .

Дадим x приращение

x , тогда y примет значение y +

y .

По

условию

F ( x + x, y + y) = 0 ,

следовательно,

полное

приращение

F = F ( x + x, y + y) − F ( x, y) = 0 , значит по определению F :

∂F

x +

∂F

y + α

x + β

y = 0 ,

где α, β

–

бесконечно малые функции

при

∂x

∂y

x, y → 0 .

∂F

∂F y

y

y

∂F

+ α

Тогда

. Отсюда

∂x

+

+ α+ β

= 0

= −

.

∂x

∂y

x

x

x

∂F

∂y

+ β

При x → 0 : α, β → 0 ;

∂F

≠ 0 по условию, и

∂y

15

∂F

dy

= −

∂x

= −

Fx′( x, y)

( ) .

dx

∂F

Fy′( x, y)

∂y

Рассмотрим

уравнение

F ( x, y, z) = 0 ,

где

F ( x, y, z)

имеет непрерывные

частные производные,

причём

∂F

≠ 0 . Оно неявно определяет функцию двух

∂z

переменных z( x, y) . Найдем

∂z

и

∂z

.

∂x

∂y

При отыскании

∂z

считаем y

постоянным, поэтому применима формула

∂x

( ) , если зависимой переменной считать x , а функцией –

z :

∂F

∂F

′

∂x

.

Аналогично:

′

∂y

.

= −

zx = −

∂F

z y

∂F

∂z

∂z

ПРИМЕР

Если x 2 + y 2 + z 2 − R 2

= 0 , то

∂z

= −

2x

= −

x

;

∂z

= −

2 y

= −

y

.

∂x

2z

z

∂y

2z

z

1.13. Локальные экстремумы функции двух переменных

ОПРЕДЕЛЕНИЕ. Функция			z = f ( x, y) имеет локальный максимум в точке
M 0 ( x0 , y0 ) ,	если	существует	некоторая	z
окрестность точки		M 0 ( x0 , y0 ) , такая, что для
всех точек	( x, y)	из этой	окрестности

выполняется неравенство f ( x0 , y0 ) > f ( x, y) .

y

x	M 0 ( x0 , y0 )

zmax = f ( x0 , y0 )

ОПРЕДЕЛЕНИЕ. Функция z = f ( x, y) имеет локальный минимум в точке

M 0 ( x0 , y0 ) , если существует некоторая

z

окрестность точки M 0 ( x0 , y0 ) , такая, что для всех точек ( x, y) из этой окрестности выполняется неравенство f ( x0 , y0 ) < f ( x, y) .

y

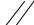M 0 ( x0 , y0 )

x

zmin = f ( x0 , y0 )

16

M 0 ( x0 , y0 )

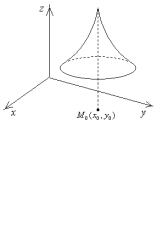
Теорема. (Необходимые условия экстремума).

Пусть есть точка экстремума функции дифференцируемой функции z = f ( x, y) . Тогда ее частные производные первого порядка в этой точке

равны нулю.

Доказательство:

	Пусть z = f ( x, y) имеет максимальное значение f ( x0 , y0 ) .
	Зафиксируем	y = y0 , получим	функцию одной переменной z1 = f ( x, y0 ) ,
	которая имеет максимум при x = x0 .
	Из теории экстремума функции одной переменной			dz1				= f x′( x0 , y0 ) = 0 .
				dx			x= x0
	Аналогично:	f y′ = ( x0 , y0 ) = 0 .
	В случае минимума доказательство аналогично.
	Таким образом, необходимые		условия экстремума в точке M 0 ( x0 , y0 )
	дифференцируемой функции f ( x, y)		имеют вид:

f x′( x0 , y0 ) = 0f y′( x0 , y0 ) = 0 .

Замечание. Функция может иметь экстремум в точке, в которой одна или обе частные производные не существуют. Например, функция z = x + y имеет минимум в точке (0, 0) и обе частные производные в этой точке не существуют,

а функция z =	x	+ y2 в точке (0, 0) имеет минимум, но	в этой точке не
существует только одна частная производная по х.
Точки, в которых частные производные первого
порядка некоторой функции равны нулю или не
существуют, называются критическими.
Геометрический смысл заключается в том, что в точке
M 0 , лежащей выше (ниже) всех соседних, поверхность
z = f ( x, y) либо имеет горизонтальную касательную
плоскость, либо не имеет касательной плоскости.
Теорема. (Достаточные условия экстремума).
Пусть в некоторой области, содержащей точку M 0 ( x0 , y0 ) ,			функция z = f ( x, y)

имеет непрерывные частные производные до третьего порядка включительно.

Пусть точка M 0 ( x0 , y0 )

является критической точкой f ( x, y) , т.е.

∂f ( x0 , y0 )

= 0

,

∂f ( x0 , y0 )

= 0 .

∂x

∂y

Введем обозначения

∂ 2 f ( x

, y

)

A ,

∂ 2 f ( x

, y

)

= B ,

∂ 2

f ( x

, y

)

= C .

0

0

=

0

0

0

0

∂x 2

∂x∂y

∂y 2

Составим дискриминант

B

= AC − B 2 .

=

A

B

C

Тогда:

17

1). Если > 0 , то функция имеет экстремум в точке ( x0 , y0 ) , причем это максимум при A < 0 и минимум при A > 0 .

2). Если < 0 , – экстремума нет.

3). Если = 0 , – требуется дополнительное исследование.

Доказательство:

По формуле Тейлора второго порядка

f (M ) = f (M 0 ) + df (M 0 ) + 1 d 2 f (M 0 ) + R2 (M ) .

2!

В критической точке f ′( x0 , y0 ) = f y′( x0 , y0 ) = 0 ,

df ( x0 , y0 ) = f x′( x0 , y0 )dx + f y′( x0 , y0 )dy = 0 ,

f ( x, y) − f ( x0 , y0 ) = f ( x0 , y0 ) , и формула Тейлора принимает вид:

f ( x0 , y0 ) = 1 d 2 f ( x0 , y0 ) + R2 ( x, y) .

2

Остаточный член R2 ( x, y ) является бесконечно малой более высокого

порядка,

чем d 2 f ( x , y

0

) , поэтому знак

f ( x

, y )

совпадает

со знаком

0

0

0

d 2 f ( x , y

) в окрестности точки ( x

, y

0

) .

0

0

0

Исследуем знак d 2 f ( x0 , y0 ) :

d 2

∂2 f ( x , y )

dx2

∂2 f ( x , y

)

∂

2 f ( x , y )

dy2

f ( x , y

) =

0 0

+ 2

0

0

dxdy + +

0 0

=

∂x2

∂y2

0 0

∂x∂y

dx

2

dx

= Adx2 + 2Bdxdy + Cdy2

= = dy 2 A

+ 2B

+ C .

dy

dy

Выражение в квадратных скобках является квадратным трехчленом с

дискриминантом D = 4B 2 − 4 AC = −4 .
1. Если > 0 ,		то D < 0	и знак квадратного трехчлена совпадает со знаком
старшего	коэффициента		A ,	значит,	знак d 2 f ( x0 , y0 ) и, следовательно, знак
f ( x0 , y0 )	совпадает со знаком A , то есть
а) если A < 0 ,		f ( x0 , y0 ) < 0		и ( x0 , y0 )	– точка максимума;
б) если A > 0 ,		f ( x0 , y0 ) > 0		и ( x0 , y0 )	– точка минимума.

2.Если < 0 , то D > 0 и знак квадратного трехчлена меняется в окрестности точки ( x0 , y0 ) и функция f ( x0 , y0 ) не имеет экстремума в точке ( x0 , y0 ) .

3.Если = 0 , то D = 0 и достаточный признак не дает ответа, нужно

выяснить сохраняется ли	знак разности	f ( x0 , y0 ) = f ( x, y) − f ( x0 , y0 )
непосредственно.
Схема исследования f ( x, y)	на экстремум:

1)определите критические точки;

2)проанализируйте выполнение достаточных условий;

3)вычислите zэкстр. .

ПРИМЕР

Исследуем на экстремум функцию z = x 2 − xy + y 2 + 3x − 2 y +1 .

18

1)

∂z

= 2x − y + 3 ,

∂z

= − x + 2 y − 2 .

∂x

∂y

2 x − y + 3 = 0,

− x + 2 y − 2 = 0,

откуда x0

= −

4

;

y0

=

1

.

3

3

2) A =

∂ 2 z

=

2 ,

B =

∂ 2 z

= −1 , C =

∂ 2 z

= 2 ,

∂x 2

∂x∂y

∂y 2

4 1

4 1

4 1

−

;

−

;

−

;

3 3

3 3

3 3

2

2

4

1

= AC − B

= 2 2

− (−1)

= 3 .

Итак,

> 0

,

A >

0 , значит −

;

–

точка

3

3

минимума, zmin

= −

4

.

3

ПРИМЕР Исследуем на экстремум функцию

z = x 2 y 2 + x 2 + y 2 + xy + 1 .

22

∂z = 2 xy 2 + x + y = 0,

1). ∂∂xz 2

= 2 yx

+ y + x = 0

∂x

x0 = y0 = 0 ;

z(0,0) = 1 .

∂ 2 z

2). A =

= 2 y 2 + 1

= 1;

∂x

2

(0,0)

(0,0 )

B =

∂ 2 z

= 4 xy + 1

= 1 ;

∂x∂y

(0,0)

(0,0)

∂ 2 z

C =

= 2x 2 + 1

= 1;

∂y

2

(0,0 )

(0,0)

= AC − B2 =

1 1

= 0 .

1

1

Достаточный признак ответа не дает. Исследуем значения z( x, y) .

z( x, y) = x 2 y 2 +

x 2

+

y 2

+ xy + 1 = ( xy)2 +

1

( x + y)2 + 1 , значит z( x, y) > 1 , если x ≠ 0 ,

2

2

2

y ≠ 0 .

Получили, что z( x, y) > z(0,0) , значит (0,0) – точка минимума, z(0, 0) = 1 .

1.14.Условный экстремум. Метод множителей Лагранжа

1.14.1.Метод исключения переменной

Найдем экстремум функции z = z (x, y), если переменные x и y связаны

условием ϕ( x, y ) = 0 .

19

Разрешая это уравнение относительно одной из переменных (х или у) и подставляя это выражение в исходную функцию, приходим к задаче поиска экстремума функции одной переменной. При этом, если уравнение ϕ( x, y ) = 0 разрешимо не однозначно – имеет несколько решений, то исследуем все решения.

ПРИМЕР. Исследуем на экстремум функцию z = x 2 + y 2 при условии x + y = 1 .

Условие связи

позволяет

исключить из

функции

z

z( x, y)

переменную y = 1 − x ,

что сводит

задачу

к

исследованию функции одной переменной

z = 2x 2 − 2 x + 1 .

dz

= 4x − 2 = 0 в точке x0

=

1

, при этом

=

1

. Так

y

y0

0

dx

2

2

x

2 z

как

d

= 4 > 0 ,

то эта точка является точкой минимума.

dx2

Таким образом,

z( x, y) достигает минимума на прямой x + y = 1 в точке

1

,

1

,

2

2

1

1

1

при этом zmin

,

=

.

2

2

2

1.14.2. Метод Лагранжа

Если из уравнения связи ϕ( x, y ) = 0 нельзя выразить одну переменную как явную функцию другой, то критические точки можно найти методом

множителей Лагранжа.
Заметим, что уравнение		z = z (x, y) определяет некоторую поверхность в
пространстве,	уравнение	ϕ( x, y ) = 0	определяет	цилиндрическую

поверхность, образующие которой параллельны оси Oz , а пересечение этих поверхностей определяет некоторую пространственную кривую. Нас интересуют точки этой кривой с экстремальными значениями координаты z .

Будем предполагать, что функции z( x, y ) и ϕ( x, y) имеют непрерывные частные производные по всем аргументам в окрестности предполагаемой критической точки до второго порядка включительно и уравнение связи ϕ( x, y ) = 0 неявно задает функцию y = y( x) . При этом z( x, y) = z( x, y( x)) и

необходимое условие экстремума принимает вид:

dz = ∂z + ∂z dy = 0 . dx ∂x ∂y dx

Так как для всех точек пространственной кривой выполняется условие ϕ( x, y ) = 0 , то при смещении вдоль кривой

d ϕ = ∂ϕ + ∂ϕ dy = 0 . dx ∂x ∂y dx

20