Arkhiv_ZIP_-_WinRAR / Chast_6_FNP

Это дает нам для нахождения координат критических точек систему уравнений

∂z

+

∂z dy

= 0,

∂x

∂y dx

∂ϕ

+

∂ϕ dy

= 0,

∂x

∂y dx

ϕ( x, y) = 0.

Исключим из системы производную неявно заданной функции dy , для dx

чего:

1) умножим второе уравнение на неопределенный множитель λ и сложим его с первым:

	∂z	+ λ	∂ϕ	+	dy		∂z	+ λ	∂ϕ		= 0 .
	∂x						∂y
			∂x dx						∂y

2) выберем коэффициент λ таким, чтобы	∂z	+ λ	∂ϕ	= 0 .
	∂y
			∂y

После преобразований получаем систему, равносильную исходной и задающую необходимые условия экстремума:

		∂z	+ λ			∂ϕ		= 0,
		∂y				∂y
		∂z	+ λ			∂ϕ		= 0,
		∂x
						∂x
	ϕ( x, y) = 0.
Если ввести функцию Лагранжа: L( x, y, λ ) = z( x, y) + λϕ ( x, y) , то задача
нахождения условного экстремума z( x, y)								сводится к исследованию на
обычный экстремум функции Лагранжа L( x, y, λ )											и необходимые условия
экстремума принимают вид:
	(x, y ,λ)=0,
Lx′				zx′(x, y)+λϕx′(x, y)=0,
	(x, y ,λ)=0,						(x, y)+λϕ′y (x, y)=0,
Ly′				z′y
	(x, y, λ)=0,
Lλ′				ϕ(x, y)=0,
откуда находятся критические точки						P		x	, y	0 )	и соответствующие значения
				0 ( 0

множителя Лагранжа λ0 .

Достаточные условия в методе Лагранжа формулируются следующим образом. Рассмотрим функцию

21

0

ϕ'

P , λ

ϕ'

P , λ

x

( 0

0 )

y ( 0

0 )

=−

'

P , λ

''

''

λ

ϕ

x (

L P , λ

L P ,

0 0 )

xx

( 0 0 )

xy

( 0 0 )

,

'

P , λ

''

''

λ

ϕ

y (

L P , λ

L

P ,

0 0 )

xy

( 0 0 )

yy

( 0 0 )

где P

x , y

0 )

, λ

0

– произвольное решение системы.

0

(

0

Тогда:

если

>0 , то в точке P

x

, y

– минимум,

0

( 0

0 )

если

<0 , то – максимум,

если

=0 , то в точке P

x

, y

0 )

экстремума нет.

0

( 0

ПРИМЕР

Исследуем на экстремум функцию z = x 2 + y 2 − 3xy при условии x + y + 1 = 0 .

L( x, y) = x 2 + y 2 − 3xy + λ( x + y + 1) .

′

= 2x − 3 y + λ ,

′

= 2 y − 3x + λ .

Lx

Ly

2 x − 3 y + λ = 0,

2λ = x + y,

2 y − 3x + λ = 0,

− y = 0,

x

1

1

1

x

= −

; y

= −

, λ =−

.

0

2

0

2

0

2

+ y + 1

= 0

+ y + 1 = 0

x

x

0

1

1

1 −3

1 2

=−

1 2 −3

=

−

=5 +5 =10.

1

−3

2

1

2

1

−3

В точке (−

1

,−

1

)

>0 , т.е. в этой точке – минимум z(x , y).

2

2

ПРИМЕР

Исследуем

на

экстремум

функцию

z = 6 − 4x − 3 y при условии, что

x 2 + y 2 −1 = 0 .

L( x, y) = 6 − 4 x − 3 y + λ( x 2 + y 2 −1)

∂L

= −4 + 2λx ;

∂L

= −3 + 2λy .

∂x

∂y

Необходимые условия экстремума:

2

x =

2λx − 4 = 0,

,

λ

3

5

2λy − 3

= 0,

y =

,

откуда λ = ±

.

x 2 + y 2

2 λ

2

= 1

2

+ y

2

=1,

x

Критические точки:

5

4

3

λ1

=

: M1 ( x1 , y1 ) = M1

;

;

2

5

5

5

4

3

λ2

= −

:

M 2 ( x2 , y2 ) = M

2

−

;−

.

2

5

5

Проверим выполнение достаточных условий:

22

∂ 2 L

= 2λ ;

∂ 2 L

= 2λ ;

∂ 2 L

= 0 ,

∂x 2

∂y 2

∂x∂y

d 2 L = 2λ (dx 2 + dy 2 )

d 2 L(M

1

) = 5(dx 2 + dy 2 ) > 0 ,

d 2 L(M

2

) = −5(dx 2 + dy 2 ) < 0 , значит

4

3

M1

;

– точка минимума, z(M1 ) = 1 ,

5

5

4

3

M 2

−

;−

– точка максимума, z(M 2 ) = 11.

5

5

1.15. Наибольшее и наименьшее значения функции в замкнутой области Теорема. Пусть функция непрерывна в замкнутой области D и дифференцируема во внутренних точках этой области. Наибольшее и наименьшее значение функции (глобальный экстремум) достигается либо в

критических точках функции внутри области, либо на границах области.

Для нахождения наибольшего и наименьшего значения функции		z( x, y) в
замкнутой, ограниченной области D следует:
1)	найти критические точки внутри D , вычислить в них z( x0 , y0 ) ;
2)	найти наибольшее и наименьшее значения функции	z( x, y)

на границе; 3) сравнить найденные значения и выбрать среди них наибольшее и наименьшее.

ПРИМЕР

Найдем наибольшее и наименьшее значения функции

z = 2x3 − 6xy + 3 y 2 в

области, ограниченной осью Oy , прямой y = 2 и параболой y =

x 2

.

2

∂z

= 6x 2 − 6 y = 0,

y

M1 (0,0) , M 2 (1,1) .

2

1. ∂x

M

∂z = −6x + 6 y = 0

2

∂y

M

1

0

2

x

Точка M 2 (1,1) – внутренняя точка области,

z1 (1,1) = −1 .

2. Рассмотрим поведение функции на границе области.

y [0,2],

2.1. x = 0,

2

- возрастающая функция,

z = 3 y

z2 (0,0) = 0 ;

z3 (0,2) = 12 .

23

x [0,2],

2.2.y = 2,

	3	− 12 x + 12,
z = 2 x

dz = 6x2 − 12 = 0 ; x = 2 [0, 2] . dx

Найдем значения

z4 (2 ,2) = 12 − 82 ; z5 (2,2) = 4 .x 2

,

2

2.3.z = 3 x 4 − x 3 ,

4

x [0,2],y =

dz	= 3x3 − 3x2 = 0 → x = 0 , x						= 1.
						2
dx					1
		1		1
z6 = 1,			= −		.
		2		4

3. Сравнивая полученные значения z , находим

,

zнаим = z(1,1) = −1 , zнаиб = z(0, 2) = 12 .

1.16.Геометрические приложения функций двух переменных

1.16.1.Уравнение касательной к пространственной кривой

1. Если линия задается параметрическим уравнением r = r (t ) , то уравнение

V

M 0 ( x0 , y0

, z0 ) записывается как уравнение

касательной к кривой r (t) в точке

V

прямой, проходящей через точку M 0

параллельно вектору

dr

.

dt

M

0

Направляющий

вектор касательной

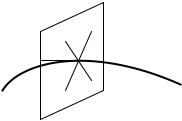
{x − x0 , y − y0 , z − z0 } и вектор

V

dx

dy

dz

dr

параллельны. Условие параллельности заключается в том,

=

,

,

dt

M

dt

dt

dt M

0

0

что компоненты этих векторов пропорциональны, эти равенства и представляют уравнение касательной:

x −

x0

=

y −

y0

=

z −

z0

*).

dx

dy

dz

dt

M

0

dt

M

0

dt

M

0

2. Пусть кривая в пространстве задана как линия пересечения двух поверхностей:

24

Φ1 ( x, y, z) = 0, L : Φ 2 ( x, y, z) = 0,

где x = x(t ) , y = y(t) , z = z(t ) .

Итак,

Φ1 [x(t), y(t), z(t)] = 0,
Φ	2	[x(t ), y(t), z(t )] = 0.

Продифференцируем эти уравнения:

∂Φ1

dx

+

∂Φ1

dy

+

∂Φ1

dz

= 0,

dt

∂y

dt

∂z

dt

∂x

∂Φ

2

dx

∂Φ

2

dy

∂Φ

2

dz

+

+

= 0.

∂y

∂z

dt

dt

dt

∂x

Получим систему двух уравнений с тремя неизвестными Найдем решение системы:

∂Φ1

dx

+

∂Φ1

dy

= −

∂Φ1

dz

,

∂y

∂z

dt

dt

dt

∂x

∂Φ

2

dx

∂Φ

2

dy

∂Φ

2

dz

+

= −

.

∂y

∂z

dt

dt

dt

∂x

dx , dy , dz . dt dt dt

По формулам Крамера:

dx

=

1

,

dt

dy

=

2

,

dt

∂Φ1

∂Φ1

где

=

∂x

∂y

,

∂Φ

2

∂Φ

2

∂x

∂y

∂Φ1

∂Φ1

∂Φ1

∂Φ1

1 = −

dz

∂z

∂y

=

dz

∂y

∂z

,

dt

∂Φ 2

∂Φ 2

dt

∂Φ 2

∂Φ 2

∂z

∂y

∂y

∂z

∂Φ1

∂Φ1

∂Φ1

∂Φ1

= −

dz

∂x

∂z

=

dz

∂z

∂x

.

2

dt

∂Φ 2

∂Φ

dt

∂Φ 2

∂Φ

2

2

∂x

∂z

∂z

∂x

25

Итак,

∂Φ1

∂Φ1

∂Φ1

∂Φ1

∂y

∂z

∂z

∂x

∂Φ 2

∂Φ 2

∂Φ

2

∂Φ

2

dx

∂y

∂z

dz

dy

dz

∂z

∂x

=

;

=

.

dt

∂Φ1

∂Φ1

dt

dt

∂Φ1

∂Φ1

dt

∂x

∂y

∂x

∂y

∂Φ 2

∂Φ 2

∂Φ 2

∂Φ 2

∂x

∂y

∂x

∂y

Решение может быть записано в виде:

dx

dy

dz

dt

=

dt

=

dt

.

∂Φ1

∂Φ1

∂Φ1

∂Φ1

∂Φ1

∂Φ1

∂y

∂z

∂z

∂x

∂x

∂y

∂Φ

2

∂Φ

2

∂Φ 2

∂Φ 2

∂Φ

2

∂Φ

2

∂z

∂x

∂y

∂z

∂x

∂y

Подставляя выражения для

dx

,

dy

,

dz

в уравнение касательной *), получим

dt

dt

dt

его в виде:

x − x0

=

y − y0

=

z − z0

, если хотя бы один из определителей

Φ′

Φ′

Φ′

Φ′

Φ′

Φ′

1 y

1z

1z

1x

1x

1 y

Φ′

Φ′

Φ′

Φ′

Φ′

Φ′

2 y

2 z

M

0

2 z

2 x

M 0

2 x

2 y

M

0

не равен нулю. Если все определители равны нулю, то точка называется особой точкой кривой.

1.16.2. Нормальная плоскость и ее уравнение

Плоскость, перпендикулярная к касательной к кривой в точке ( x0 , y0 , z0 ) ,

называется нормальной плоскостью.

Уравнение плоскости, которая перпендикулярна

касательной к кривой, имеет вид уравнения

плоскости, проходящей через точку ( x0 , y0 , z0 ) , с

нормальным вектором

dr

:

dt

M

0

а) в случае параметрического задания:

dx

( x − x0 ) +

dy

( y − y0 ) +

dz

( z − z0 ) = 0 ;

dt

M

dt

M

dt

M

0

0

0

26

б) если кривая задана пересечением двух поверхностей:

Φ′

Φ′

Φ′

Φ′

1 y

1z

( x − x0 ) +

1z

1x

( y − y0 ) +

Φ′

Φ′

Φ′

Φ′

2 y

2 z

M

0

2 z

2 x

M

0

Φ′

Φ′

+

1x

1 y

( z − z

0 )

= 0 .

Φ′

Φ′

2 x

2 y

M

0

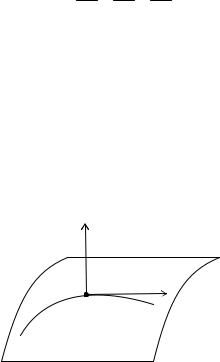
1.16.3. Касательная плоскость и нормаль к поверхности

Пусть поверхность задана уравнением F ( x, y, z) = 0 ) .

ОПРЕДЕЛЕНИЕ. Точка M ( x, y, z) называется обыкновенной, если все три

частные производные ∂F , ∂F , ∂F существуют, непрерывны и хотя бы одна из

∂x ∂y ∂z

них отлична от нуля.

ОПРЕДЕЛЕНИЕ. Точка M ( x, y, z) называется особой точкой поверхности, если все три частные производные равны нулю или хотя бы одна из них не

существует.

ОПРЕДЕЛЕНИЕ. Прямая линия называется касательной к поверхности в точке M ( x, y, z) , если она является касательной к какой-либо кривой, лежащей на поверхности и проходящей через точку M .

R n

R a

M

L

Теорема. Все касательные прямые к данной поверхности в ее обыкновенной точке M лежат в одной плоскости.

Рассмотрим на поверхности произвольную линию L , проходящую через обыкновенную точку M 0 ( x0 , y0 , z0 ) :

x = x(t),

L : y = y(t), )z = z(t).

Касательная к этой кривой будет касательной и к поверхности. Уравнения касательной в точке M 0 ( x0 , y0 , z0 ) имеют вид:

x −

x0

=

y −

y0

=

z −

z0

.

dx

dy

dz

dt

M

0

dt

M

0

dt

M

0

27

Подставим уравнения L ) в уравнение поверхности ) :

F [x(t), y(t), z(t)] = 0 .

Продифференцируем полученное тождество по t , получим, что

∂F dx + ∂F dy + ∂F dz = 0 . ∂x dt ∂y dt ∂z dt

Рассмотрим вектор касательной к кривой L :

V

V

dr

=

dx

dy

dz

и вектор

V

∂F

∂F

∂F

a

=

,

,

n

=

,

,

.

dt dt

dt dt

∂x ∂y

∂z

Скалярное произведение этих векторов имеет вид:

V V

∂F dx

∂F dy

∂F dz

.

(n a) =

+

+

∂x dt

∂y dt

∂z

dt

Выше показано, что это выражение равно нулю, значит, вектор n перпендикулярен вектору a в точке M 0 ( x0 , y0 , z0 ) . Так как кривая L произвольна

и касательная к ней, проходящая через точку M 0 , перпендикулярна вектору n ,

построенному в точке M 0 , то касательные к любой кривой, проходящей через точку M 0 , лежат в одной плоскости. Эта плоскость проходит через точку M 0 и

V ∂F ∂F ∂F

перпендикулярна вектору n . Вектор n = ∂x , ∂y , ∂z называется вектором нормали к поверхности F ( x, y, z) = 0 .

ОПРЕДЕЛЕНИЕ. Плоскость, в которой расположены все касательные прямые к линиям на поверхности, проходящим через данную точку, называется

касательной плоскостью к поверхности.

Уравнение

касательной

плоскости к поверхности F ( x, y, z) = 0 в точке

M 0 ( x0 , y0 , z0 ) имеет вид:

∂F

( x − x ) +

∂F

( y − y ) +

∂F

( z − z

) = 0 .

∂x

0

∂y

0

∂z

0

M 0

M

0

M 0

Если поверхность задана явно: z = f ( x, y) , то z − f ( x, y) = 0 ,

∂F

= −

∂f

,

∂F

= −

∂f

,

∂F

= 1 , и уравнение касательной принимает вид:

∂x

∂x

∂y

∂y

∂z

z − z

=

∂f

( x − x ) +

∂f

( y − y ) .

0

∂x

0

∂y

0

M 0

M

0

ОПРЕДЕЛЕНИЕ. Прямая, проведенная через точку M ( x, y, z) поверхности перпендикулярно касательной плоскости, называется нормалью к поверхности.

Уравнения нормали имеют вид:

28

x −

x0

=

y −

y0

=

z −

z0

,

∂F

∂F

∂F

∂x

∂z

M

0

∂y

M 0

M

0

x − x0

=

y − y0

=

z − z0

.

−

∂f

−

∂f

1

∂x

M

0

M 0

∂y

1.16.4. Примеры геометрических приложений функций нескольких переменных

ПРИМЕР Напишем уравнение касательной и уравнение нормальной плоскости к

винтовой линии:

x = a cos t,y = a sin t,z = amt.

dx

= −a sin t ,

dy

= a cos t ,

dz

= am .

dt

dt

dt

Уравнения касательной:

x − a cos t

=

y − a sin t

=

z − amt

.

− a sin t

a cos t

am

Уравнение нормальной плоскости:

− a sin t( x − a cos t ) + a cos t ( y − a sin t) + am( z − amt) = 0 .

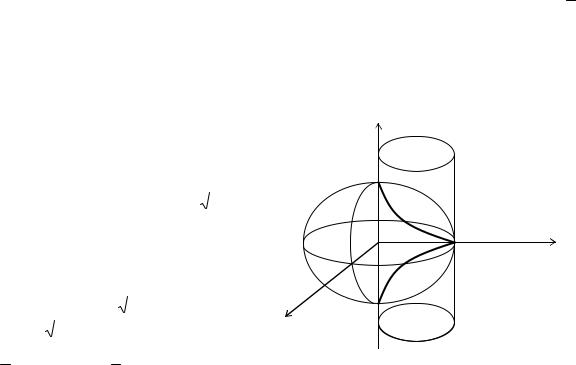
ПРИМЕР Найдем уравнения касательной и уравнение нормальной плоскости к линии

пересечения сферы x 2 + y 2 + z 2 = 4r 2 и цилиндра x 2 + y 2 = 2ry в точке M 0 (r, r, r 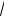2 ) .

Здесь Φ ( x, y ,z ) = x2 + y2 + z 2 − 4r 2 , Φ

2

( x, y, z) = x 2

+ y 2

− 2ry .

1

∂Φ1

= 2x ,

∂Φ1

= 2 y ,

∂Φ1

= 2z ;

∂x

∂y

∂z

∂Φ 2 = 2x ,

∂Φ 2 = 2 y − 2r , ∂Φ 2 = 0 .

z

∂x

∂y

∂z

Значения производных в точке M :

∂Φ1

∂Φ1

∂Φ1

= 2r ,

= 2r ,

= 2r 2 ;

∂x

∂y

∂z

∂Φ 2 = 2r ,

∂Φ 2 = 0 ,

∂Φ 2 = 0 .

O

2 r

y

∂x

∂y

∂z

Уравнения касательной:

x − r

=

y − r

=

z − r 2

.

x

0

2

−1

Уравнение нормальной плоскости:

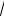2 ( y − r ) − ( z − r 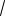2 ) = 0 .

29

ПРИМЕР Напишем уравнение касательной плоскости и уравнение нормали к

поверхности шара x 2 + y 2 + z 2 = 14 в точке P(1,2,3) .

F ( x, y, z) = x 2 + y 2 + z 2 −14 = 0 .

∂F = 2 x ; ∂F = 2 y ; ∂F = 2 z .

	∂x		∂y			∂z
В точке P(1,2,3) :
	∂F	= 2 ;	∂F	= 4 ;	∂F		= 6 .
	∂x		∂y			∂z

Уравнение касательной плоскости:

2( x − 1) + 4( y − 2) + 6( z − 3) = 0 ↔ x + 2 y + 3z − 14 = 0 .

Уравнения нормали:

x −1 = y − 2 = z − 3 ↔ x −1 = y − 2 = z − 3 .

2 4 6 1 2 3

30