Arkhiv_ZIP_-_WinRAR / Chast_6_FNP

2. ПРАКТИЧЕСКИЕ ЗАНЯТИЯ

Область определения. Предел. Непрерывность ФНП

№ п/п	Задание			Ответ
	Найдите	область	определения	функции

z 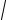y x .

РЕШЕНИЕ

Областью определения функции z y x

является множество точек, определяемое неравенством y x 0 , y x :

№1

- надграфик прямой y x , включающий границу.

Найдите	область	определения функции
z ln x2 y
РЕШЕНИЕ
Областью	определения	функции z ln x2 y

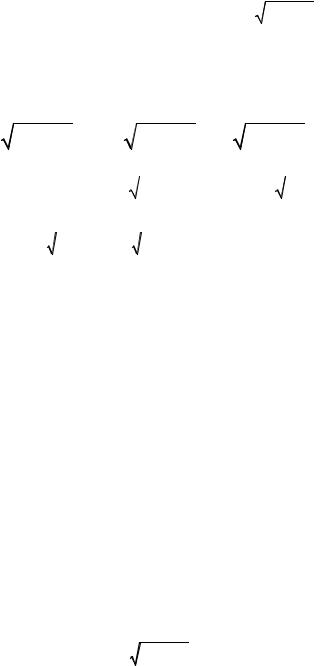
является открытое множество y > −x2 ,

№2

31

которое представляет собой точки плоскости,

лежащие строго выше параболы y = −x2 .

Вычислите предел функции z

2x2 y2

при

x2 y2

x →0, y →0 .

РЕШЕНИЕ

№3

Преобразуем

функцию

к

виду

2x2 y2

x

y

0

2x

y

.

x2 y2

x2 y2

x2 y2

Так как 1

x

1 и 1

y

1,то

x2 y2

x2 y2

x

y

lim

2x

y

0 .

2

2

2

2

x 0

x

y

x

y

y 0

Вычислите предел функции

z

2x2 y2

при

x2 y2

x →0, y →0 .

РЕШЕНИЕ

стремится

к

точке

Пусть

точка

M (x, y)

№4

M 0 (0,0) . Рассмотрим изменение x и y

вдоль

предела

прямой y = kx .

нет

Получим, что lim z lim

2x2

y2

2 k2 .

x 0

x 0

x2 y2

1 k2

y 0

Результат имеет различные значения в

зависимости от

выбранного k , т.е. зависит от

пути приближения к точке (0,0) , и поэтому

функция не имеет предела в точке (0,0).

Исследуйте

на

непрерывность

функцию

z 0,0 0,

z x, y

2x

2

y

2

.

x, y

, x

2

2

0 .

z

y

x

2

y

2

№5

непрерывна

РЕШЕНИЕ

Функция z x, y

имеет в точке (0,0) значение

нуль и предел, равный нулю, значит, непрерывна

на всей плоскости.

Исследуйте

на

непрерывность

функцию

№6

z 0,0 0,

(0,0) - точка

z x, y

2x

2

y

2

2

2

.

разрыва

x, y

, x

0 .

z

y

x

2

y

2

32

РЕШЕНИЕ

Функция z x, y имеет в точке (0,0) значение

нуль, но предел в этой точке не существует, значит, функция разрывна

в точке (0,0).

Частные производные первого порядка. Дифференциал ФНП

Найдите

частные

производные

функции

z x4 cos y y3

по

каждой

из

независимых z 4x3 cos y ;

№7

переменных.

x

РЕШЕНИЕ

z x4 cos y y3 .

z

4

sin y 3y

2

z 4x3 cos y ;

z

x4 sin y 3y2 .

y x

x

y

Найдите

частные

производные

функции

z = xy ln(x + y)

по

каждой

из

независимых

переменных.

∂ z

= y ln(x + y) + xy

1

,

№8

РЕШЕНИЕ

∂ x

x + y

∂ z

= x ln(x + y) + xy

1

.

∂ z

1

,

∂ y

x + y

= y ln(x + y) + xy

∂ x

x + y

∂ z

= x ln(x + y) + xy

1

.

∂ y

x + y

Найдите производные сложной функции z = veu ,

где

u = x + y, v = x cos y + y sin x

по

каждой из

независимых переменных.

РЕШЕНИЕ

∂z

u

u

(cos y + y cos x),

№9

∂x

= ve

+e

∂ z

= veu 1+ eu (−xsin y +sin x)

∂ z

∂ z

∂u +

∂ z

∂v

∂ y

=

= veu 1 + eu (cos y + y cos x).

∂ x

∂v

∂ x

∂u

∂ x

∂∂ zy = ∂∂uz ∂∂uy + ∂∂vz ∂∂vy = veu 1 + eu (− x sin y + sin x).

Найдите

производную

1

сложной

функции

d z

1

z = sin x ln y , где x = t, y =

.

= cos x ln y

+

d t

2

№10

t

t

РЕШЕНИЕ

+sin x

1

1

−

y

d z

∂ z

d x

∂ z

d y

1

1

1

2t

t

=

+

= cos x ln y

+ sin x

−

.

d t

∂ x

d t

∂ y

d t

y

2

t

2t t

33

Найдите

производную

сложной

функцииz sin u2

u

,

u = ex+y2

, υ = x2 + y .

РЕШЕНИЕ

Вычислим

∂z

и

∂z

.

∂x

∂y

z 2u cos

u2

u

,

z

cos u2

u

;

u

u

∂z = 2cos(u2 +v)

∂u

x+y2

∂u

x+y2

;

∂x

№11

∂x

= e

, ∂y =

2ye

(u ex+y2 + x),

∂υ

∂υ

∂z

2

= 2x ,

=1;

∂y = cos(u

+υ)

∂x

∂y

z 2u cos

u2 u

ex y2 cos

u2 u

2x

(4uyex+y2

+1)

x

x ;

2cos u2 u u ex y2

z 2u cos u2 u 2yex y2 cos u2 u

y

cos u2 u 4uyex y2 1 .

Вычислите производную неявной

функции

x2 y2 z2 ln z .

РЕШЕНИЕ

F(x, y, z) = 0 : ∂z

= −

Fx′

; ∂z

= −

Fy′

;

∂z

= −

2xz

,

∂x

2z2 −1

№12

Fz′

Fz′

∂x

∂y

∂z

= −

2yz

x2 y2 z2 ln z 0 ;

∂y

2z2 −1

z

2x

2xz

; z

2y

2yz

.

x

2z2 1

1

2z2 1

1

y

2z z

2z z

Вычислите

производную

неявной

функции

arctg xy = ln x2 + y2 .

РЕШЕНИЕ

Обозначим F(x, y) = arctg xy −ln 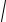x2 + y2 .

№13

∂ F

∂ y

=

x + y

dy

∂ x

x − y

∂ x

Тогда

= −

;

dx

∂ F

∂ y

∂ F

=

1

− y

−

1

1

2x =

∂ x

y 2

x2 + y2

x2

1

x2

2

+ y2

+

x

34

=

− y

−

x

=

− y − x

;

x2 + y2

x2 + y2

x2 + y2

∂ F

=

1

1 −

1

−

1

2 y =

∂ y

y 2

1 +

x

x

2 + y2

2

x2

+ y2

x

=

x

−

y

=

x − y

,

x2 + y2

x2 + y2

x2 + y2

−y − x

d y

= −

x2

+ y2

=

x + y

.

d x

x

− y

x

− y

x2 + y2

Вычислите производную неявной функции

x2 − 2 y2 + z2 − 4x + 2z −5 = 0 .

РЕШЕНИЕ

Обозначим F(x, y, z) = x2 −2y2 + z2 −4x + 2z −5 .

Тогда

№14

∂ z

∂ F

∂ z

∂ F

∂ z

= −

x − 2

;

∂ z

=

2 y

= −

∂ x

;

= −

∂ y

.

∂ x

z +1

∂ y

z +1

∂ x

∂ F

∂ y

∂ F

∂ z

∂ z

∂ F

= 2x − 4;

∂ F

= −4 y;

∂ F

= 2z + 2 .

∂ x

∂ y

∂ z

∂ z

= −

2x − 4

= −

x − 2

;

∂ z

= −

− 4 y

=

2 y

.

∂ x

2z + 2

z +1

∂ y

2z + 2

z +1

Найдите дифференциал функции z 2x2 y2.

РЕШЕНИЕ

№15

dz = ∂z dx + ∂z dy ,

∂x

∂y

dz 4xdx 2ydy

z 4x ,

z 2y ,

x

y

dz 4xdx 2ydy .

Вычислите приближенное значение (1,02)3,01 .

РЕШЕНИЕ

Функция имеет вид: z = x y . Из приближенного равенства

№16

z(x0

+∆x, y0 +∆y) ≈ z(x0 , y0 ) +

∂z

∆x +

∂z

) ∆y

1,06

∂x

( x0 ,y0 )

∂y

( x ,y

при

0

0

x0 1,

y0 3 ,

x 0,02 ,

y 0,01

получаем

z(x0 , y0 ) 1,

35

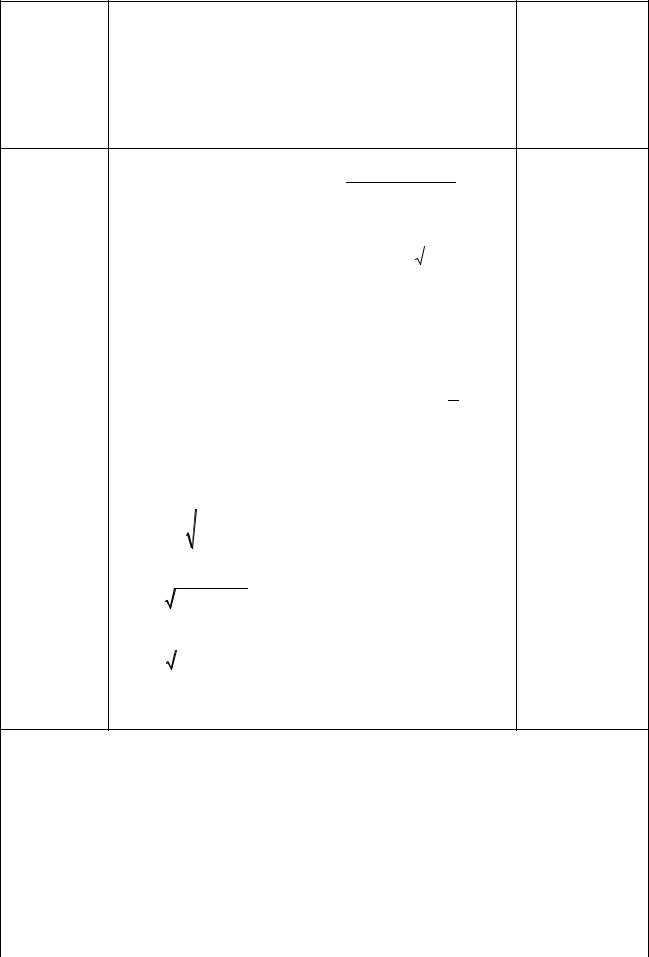
	∂z	= yxy−1 ,	z				3 1 3 ;
	∂x		x		(1,3)
	∂z	= x y ln x , z					1 ln1 0 ,
	∂y
			y				(1,3)

получаем

(1,02)3,01 1 3 0,02 1,06 .

Вычислите приближенно, заменяя приращение функции дифференциалом 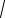sin2 1.55 +8e0.015 .

РЕШЕНИЕ

Введем	функцию								z(x, y) =		.
										sin2 x +8ey
Приближенное					значение					функции
z(x, y) ≈ z(x0 , y0 ) + dz(x0 , y0 ) =
= z(x0 , y0 ) +	∂ z			dx +	∂ z				dy .
	∂ x				∂ y
			(x	, y )				(x	, y )
	0			0	0				0

Вкачестве точки (x0 , y0 ) выберем точку π,0 .

2

№17

Тогда

dx = ∆x = x − x0 =1.55 −

π

,

3.02

2

dy = ∆y = y − y0 = 0.015 .

π

2

π

0

,

z

,0

=

sin

+8e

= 3

2

2

∂ z

=

2sin x cos x

= 0 ;

∂ x

2

sin

2

x +8e

y

π

,0

2

∂ z

=

8ey

=

4 ;

∂ y

2

sin

2

x +

8e

y

π

3

,0

2

z(1.55, 0.015) ≈ 3 +0

−1.55

π

4

0.015 ≈ 3.02 .

+

+

2

3

Частные производные и дифференциалы высших порядков.

Формула Тейлора

Вычислите производные второго порядка

2

z 6xy2 4y ,

функции z x3 y2 2x2 y 6 .

РЕШЕНИЕ

x2

2 z

3

,

№18

z 3x2 y2 4xy ; 2 z 6xy2

4y

y2

2x

x

x2

∂2 z

= 6x2 y + 4x .

∂2 z

2

y + 4x ;

=

6x

∂x∂y

∂y∂x

36

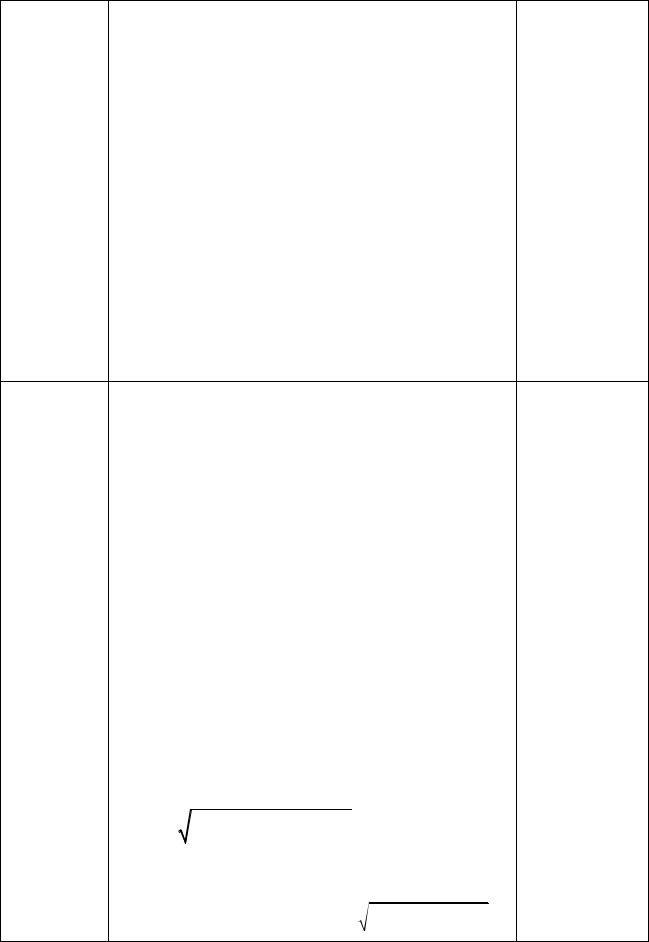
z

2x3 y 2x3 ; 2 z

2x3

y

y2

∂2 z

= 6x2 y

+ 4x .

∂x∂y

Вычислите

производные

второго порядка

функции z y2 ln x , x > 0 .

РЕШЕНИЕ

zx

y2

; zy

2y ln x ,

z′′xx = −

y2 ,

x

x

2

y2 ′

№19

′′

y2

z′′yy = 2ln x ,

=

= −

2y

zxx

2 ,

z′′

= z′′

=

.

x x

x

y2 ′

xy

yx

x

2ln x ,

2y

,

zyy 2y ln x y

z′′xy =

=

x

x y

z′′yx = (2y ln x)′x =

2y

, z′′yx = z′′xy

x

Найдите d 2 z , если z x3 y2 . РЕШЕНИЕ

d

2

z

∂2 z

2

∂2 z

∂2 z

2

=

(dx)

+

2

dxdy +

(dy)

,

∂x

2

∂x∂y

∂y

2

d

2

z

2

dx

2

+

z

= 6xy

№20

3x2 y2 ,

z

2y x3 ,

2 z

6x y2 ,

+12yx2dxdy +

x

y

x2

+2x3dy2 .

2 z

2x

3

,

2 z

6y

x

2

,

y

2

x y

d 2 z = 6xy2dx2 +12yx2dxdy + 2x3dy2 .

Запишите

формулу

Тейлора

для

функции

z = xy2

в окрестности точки

P(1,1)

до членов

первого порядка включительно. РЕШЕНИЕ Формула Тейлора с точностью до членов первого порядка:

№21	f (x, y) = f (x0 , y0 ) +dz					M0	+o(ρ),
где ρ =	(x − x )2 +(y − y	0	)2	.
	0
Вычисляя частные производные							f (x, y) xy2 в
точке (1,1), получаем:

xy2 =1+11! (x −1)+ 2(y -1) +o 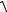(x −1)2 +(y −1)2 .

37

Геометрические приложения. Экстремумы ФНП. Наибольшее и наименьшее значения функции в замкнутой области

Для

данной

поверхности

x2 + y2 + z2

=169

составьте уравнение касательной плоскости и

нормали в точке M (3,4,12) .

РЕШЕНИЕ

Перепишем

уравнение

поверхности

в

виде

F(x, y) = x2 + y2

+ z2

−169 = 0 .

Тогда уравнение

касательной плоскости будет иметь вид

∂ F

(x − x0 ) +

∂ F

( y − y0 ) + ∂ F

(z − z0 ) = 0 ,

∂ x

M

∂ y

M

∂ z

M

где M (x0 , y0 , z0 ) .

№22

Отсюда 2x

M (x

− x0 ) + 2 y

M ( y − y0 ) + 2z

M (z − z0 ) ,

3x + 4 y +12z −169 = 0

x − 3

=

y − 4

=

z −12

6(x − 3) +8( y − 4) + 24(z −12) = 0 ,

3

4

12

6x + 4 y +12z −169 = 0 ,

3x + 4 y +12z −169 = 0 .

Уравнение нормали имеет вид:

x − x0

=

y − y0

=

z − z0

.

∂ F

∂ F

∂ F

∂ x

M

∂ y

M

∂ z

M

Отсюда

x − 3

=

y − 4

=

z −12

,

6

8

24

x − 3

=

y − 4

=

z −12

.

3

4

12

Исследуйте

на

экстремум

функцию

z = xy −

1

.

2(x + y)

РЕШЕНИЕ

1) Найдем стационарные точки:

№23

∂ z

= y +

1

= 0,

Экстремума

нет

∂ x

2(x + y)

2

1

∂ z

= x +

= 0,

2

∂ y

2(x + y)

x = y x +

1

= 0 x3 = − 1

x = −

1 x = y = −

1 .

8x2

8

2

2

Таким

образом,

функция

имеет

одну

38

критическую точку		−	1	;−	1
	P		2		2	.

2) Найдем вторые производные

A =

∂2 z

= −

1

B =

∂2 z

=1−

1

= 2 ,

=1,

∂ x2

(x + y)3

∂x∂y

(x + y)3

P

P

∂2 z

C =

= −

1

=1 .

∂ y2

(x + y)3

P

Строим из коэффициентов А, В, С определитель второго порядка

∆ =		A B		=		1	2		= −3 < 0
		B C				2	1

экстремума в точке P нет.

Исследуйте на максимум и минимум функцию

z = e2 x (x + y2 − 2 y).

РЕШЕНИЕ

1) Найдем точки, в которых может быть экстремум, используя необходимое условие экстремума:

∂ z

= e

2 x

(2x +

2 y

2

− 4 y +

1)= 0,

∂ x

∂ z

= e2 x (2 y − 2)= 0.

∂ y

Из второго уравнения y =1 2x −1 = 0 x =

1 .

№24

2

1

e

Следовательно,

функция

имеет

одну

zmin

,1

= −

2

2

критическую точку

1

P

2

,1 .

2) Выясним, существует ли экстремум в этой

точке. Для этого вычислим вторые производные:

A =

∂2 z

= e2 x (4x + 4 y2 −8y + 4)

= 2e ,

∂ x2

P

B =

∂2 z

= e2x (4y −4)

=

0 ,

∂x ∂y

P

C =

∂2 z

= e2x 2

= 2e .

∂y2

P

Вычислим определитель второго порядка

39

∆ =

2e

0

= 4e

2

> 0

в точке

1

z

0

2e

P

2

,1 функция

имеет экстремум.

Так как A > 0 , этот экстремум – минимум.

1

e

.

zmin

,1 = −

2

2

Исследуйте на экстремум функцию

z y4 4y2

y2 4x 4y , x 0 .

x

РЕШЕНИЕ

z

2y

2

4 0,

x

1).

x

z

3

4y

8y

x 2y 4 0

y

2 ;

z(4, 2) 4 .

x0

4, y0

2). A

2 z

y2

1 ;

x2

№25

(4, 2)

x x

(4, 2)

2

zmin (4,−2) = −4

2 z

B

4

y

4 ;

x y

(4, 2)

x 4, 2

C 2 z2

12y2 8

34 ;

x

2

y

(4, 2)

(4, 2)

1

34 −42 =1 > 0.

∆ = AC − B2 =

2

1 0 – минимум.

Экстремум есть, A

2

(4, 2)

– точка минимума, zmin (4,−2) = −4 .

Найдите условные экстремумы функции z = −2xy

при условии − x + 2 y =1 .

РЕШЕНИЕ

Обозначим

ϕ(x, y) = −x + 2y −1.

Составим

функцию Лагранжа L = −2xy + λ (−x + 2 y −1) .

1

1

1

№26

Найдем ее критические точки:

−

,

=

zmax

2

4

4

∂ L

=

−2 y − λ = 0,

∂ x

∂ L

= −2x + 2λ

= 0,

∂ y

∂ L

=

(− x + 2 y

−1)= 0.

∂λ

40