§4. Степенные ряды

1.Степенной ряд и область его сходимости

Определение. Степенным рядом называется ряд вида

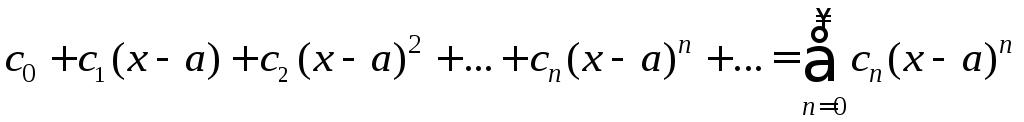, (I)

где постоянные,х- переменная. Число а называется центром ряда, числа c_n- коэффициентами ряда.

Например, 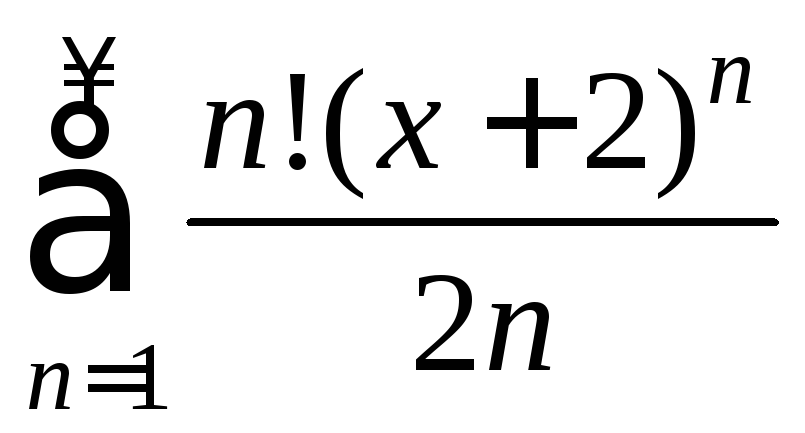, 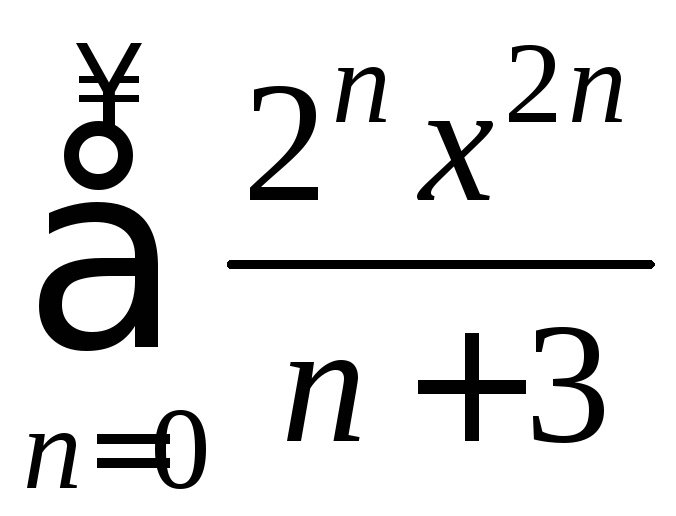- степенные ряды, а 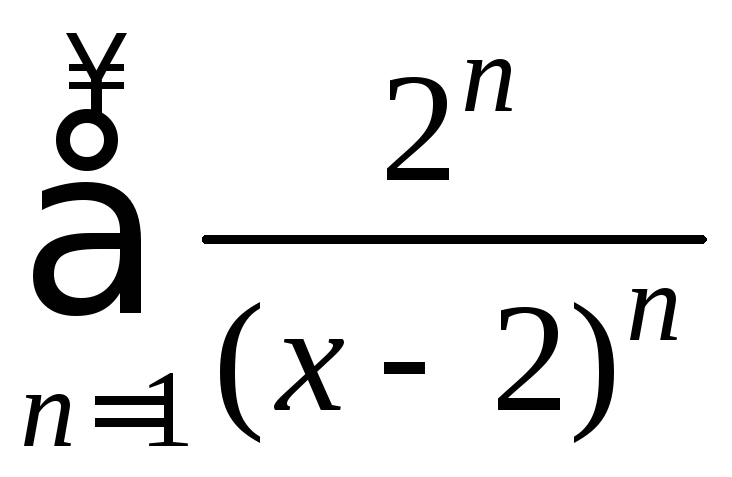, - не степенные ряды.

Обозначим x-a=t, из (I) получим ряд 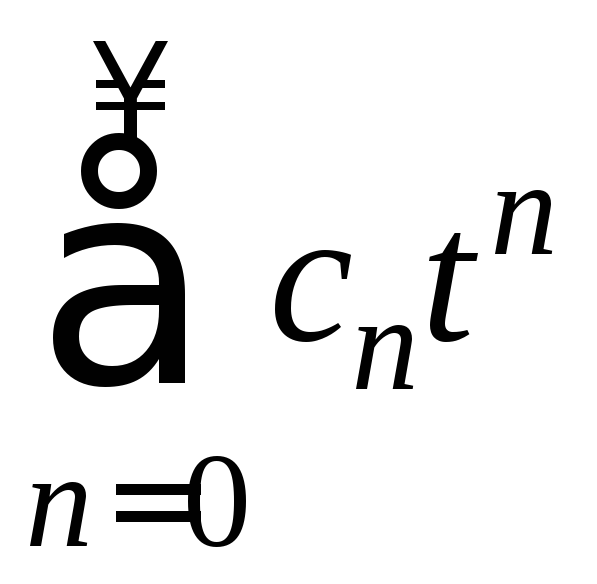. (II)

Очевидно, что исследование сходимости ряда (I) равносильно исследованию ряда (II). Поэтому далее будем рассматривать ряд

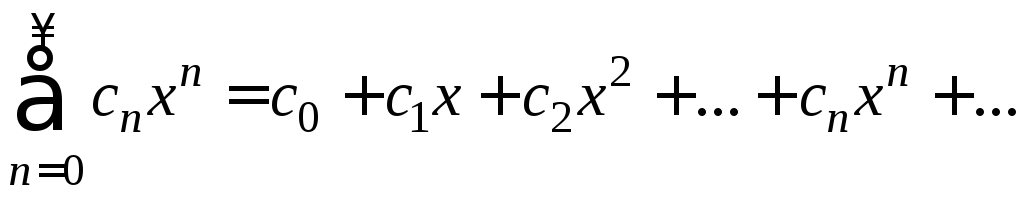(1)

Члены ряда (1) определены и непрерывно дифференцируемы на . Ряд (1) всегда сходится в точкеx=0 и S(0)=c₀, то есть область сходимости степенного ряда (1) . Выясним вид (структуру) области сходимости степенного ряда.

Теорема 1 (Абеля). Пусть дан степенной ряд (1)

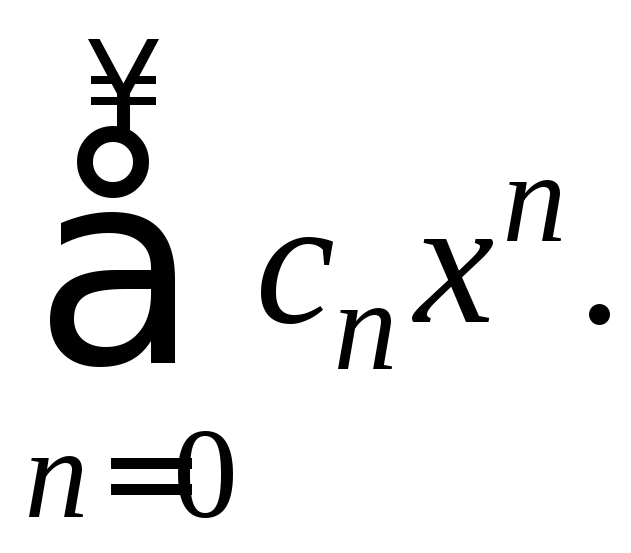
1. если ряд (1) сходится для некоторого значения 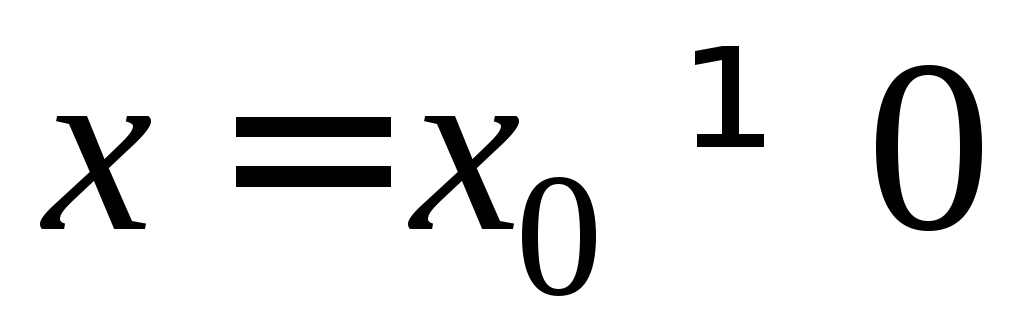, то он сходится абсолютно, такого что;

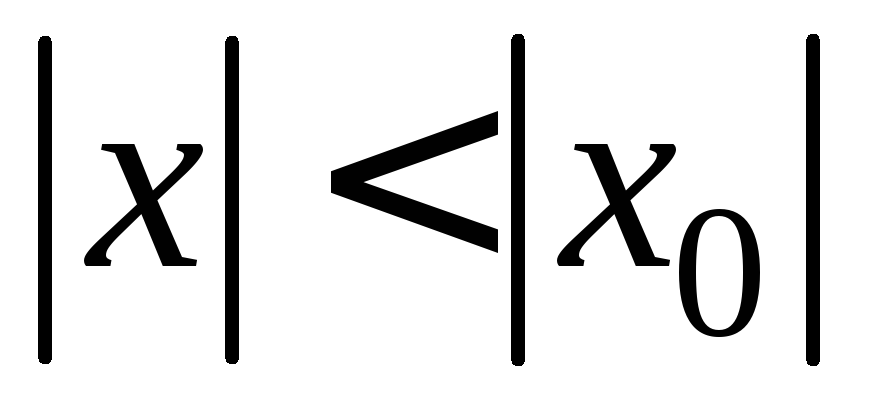2. если ряд (1) расходится для некоторого значения 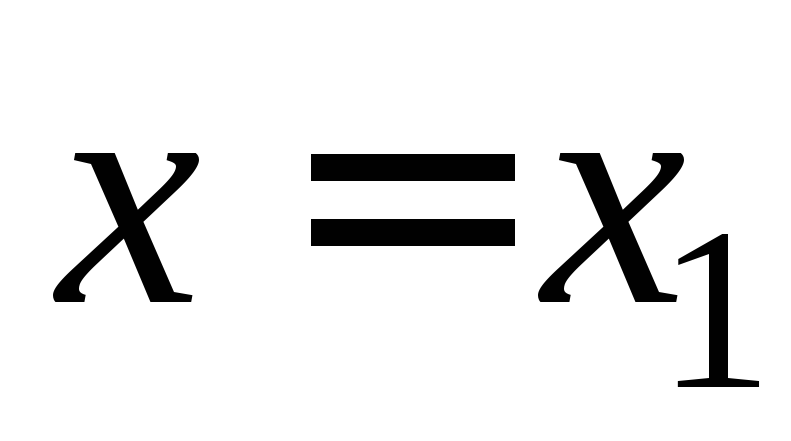, то он расходится и, такого что.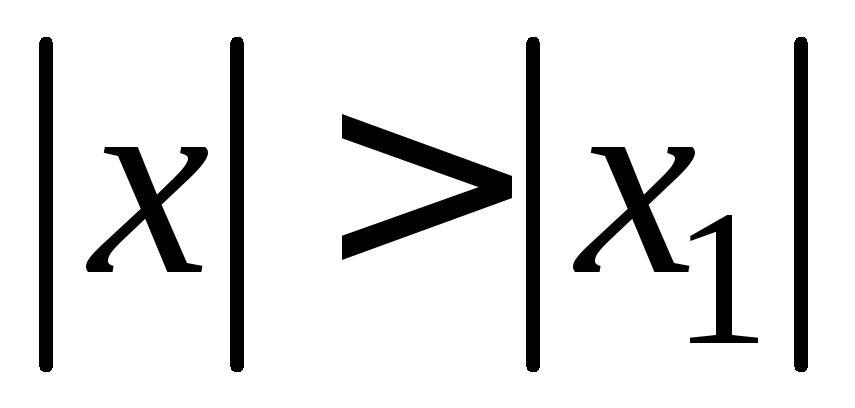

Доказательство.

1) По условию ряд (1) сходится в точке x=x₀, то есть сходится ряд 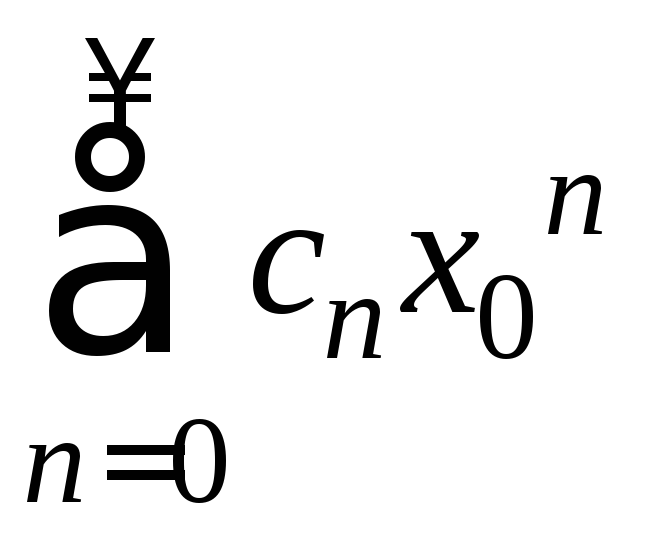По необходимому условию сходимости это означает, что. Так как последовательностьимеет предел, то она ограничена, то есть:имеет место неравенство.

Возьмем :, тогда

.

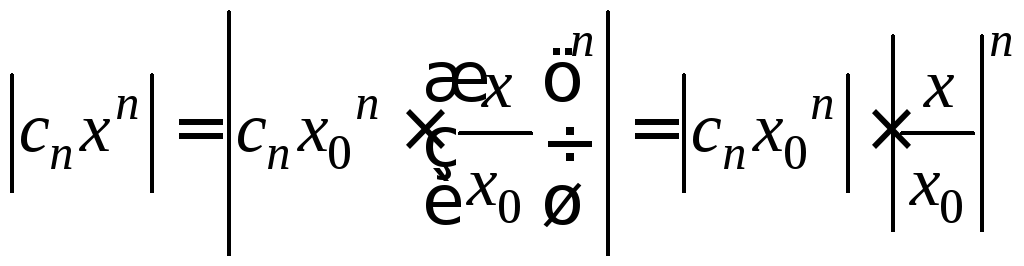Обозначим , тогда

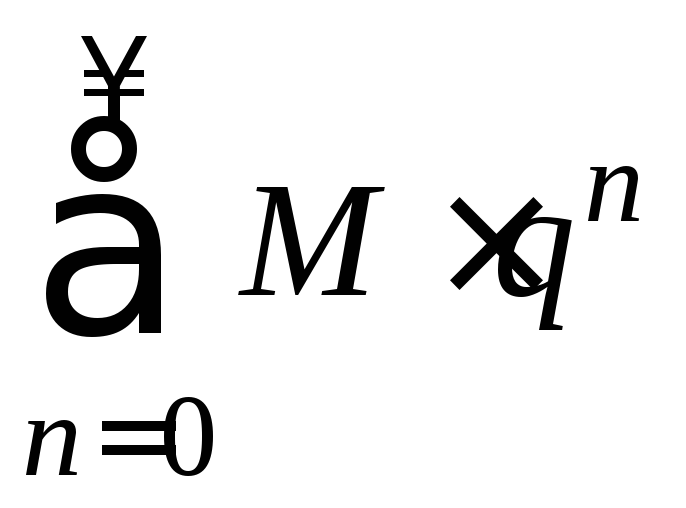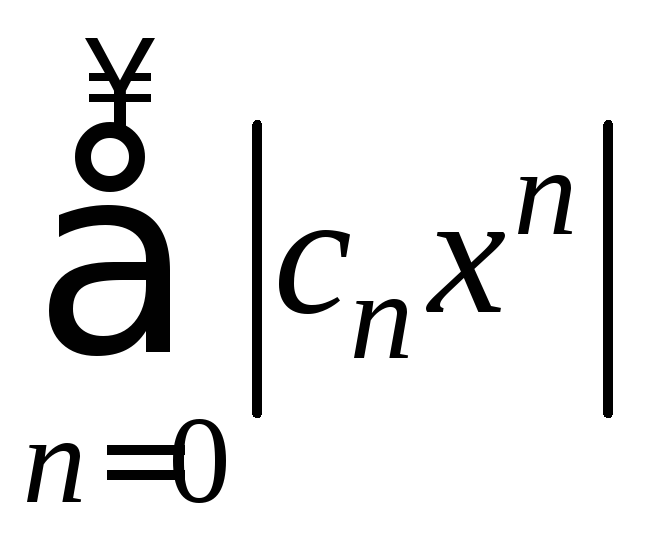
Ряд сходится (как геометрический со знаменателемq<1). Тогда по общему признаку сравнения сходится ряд :. Поэтому, ряд (1) сходится абсолютно:.

2) Пусть ряд (1) расходится для некоторого значения . Допустим противное: что:ряд сходится. Тогда по доказанному ряд должен сходится и при. Это противоречит условию. Значит, наше допущение неверно и:ряд (1) расходится.

С геометрической точки зрения теорема 1 утверждает следующее:

1. если ряд (1) сходится в точке х₀, то он сходится в интервале ;

2. если ряд (1) расходится в точке , то он расходится во всех точках, которые расположены дальше от начала отсчета, чем, то есть в интервалах

Рассмотрим степенной ряд (1) Для него возможны три случая:

1. ряд (1) сходится на всей числовой оси;

2. ряд сходится только в точке

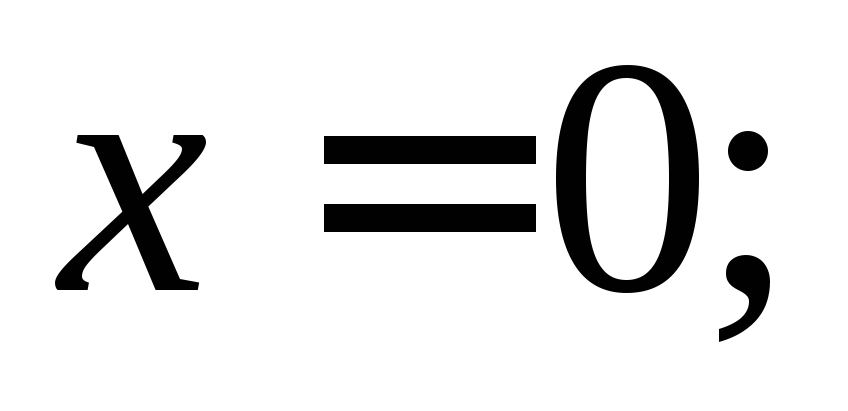
3. ряд сходится не только в точке 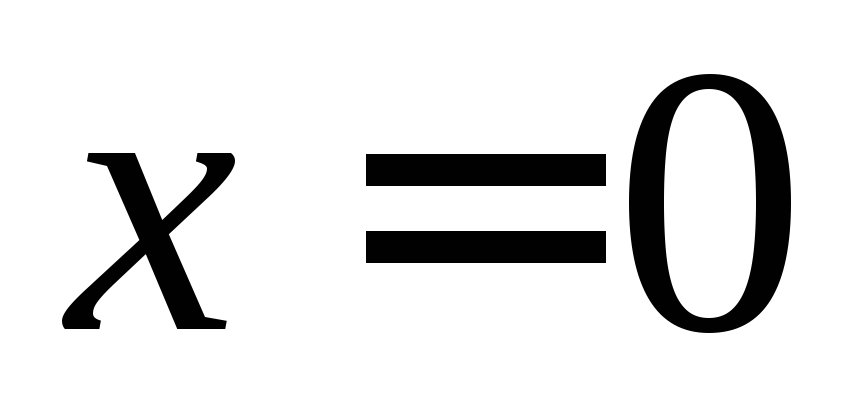, но и не на всей числовой оси.

Для третьего случая имеет место следующая теорема.

Теорема 2. Если ряд (1) сходится не на всей числовой оси, но и не только в точке , то существует числотакое что

1) ряд абсолютно сходится при любом значении ,;

2) ряд расходится при любом значении ,.

Доказательство.

Обозначим через множество всех значений, при которых ряд (1) сходится (по условию оно не пусто и не). Следовательно,- ограничено. Действительно, возьмем точку, в которой ряд (1) расходится (по условию она существует). Тогда по теореме Абеляудовлетворяет неравенству. Следовательно,М ограничено. Любое ограниченное множество имеет верхнюю грань. Обозначим её .

1) Возьмем х: . По определению точной верхней грани:. Так как в точкех₀ ряд (1) сходится, то по теореме Абеля, он абсолютно сходится в точке х.

2) Возьмем х: асодержит все возможные значениях, где ряд (1) сходится. Поэтому, в точке х ряд (1) расходится.

Определение. Число определенное в теореме 2, называетсярадиусом сходимости степенного ряда. Промежуток называетсяинтервалом сходимости (абсолютной) степенного ряда (1).

Если ряд (1) сходится на , то полагают.

Если ряд (1) сходится в точке , то

Таким образом, всякий степенной ряд имеет свой радиус сходимости R.

Сходимость на концах интервала сходимости, то есть в точках , в каждом конкретном случае исследуется отдельно. В этих точках ряд может как сходится, так и расходится.

Таким образом, область сходимости степенного ряда (1) может представлять собой:

1. интервал (к которому может быть присоединён один из его концов или оба) - симметричный относительно точки 0;

2. вся числовая ось;

3. только точка .