
- •II. Функциональные последовательности и ряды
- •§1. Функциональная последовательность и функциональный ряд. Область сходимости
- •§2. Равномерная сходимость функциональных последовательностей и рядов
- •1. Равномерная сходимость функциональной последовательности
- •2. Критерий равномерной сходимости функциональной последовательности
- •3. Равномерная сходимость функциональных рядов
- •4. Достаточный признак равномерной и абсолютной сходимости
- •§3. Основные свойства равномерно сходящихся последовательностей и рядов
- •1. Непрерывность суммы равномерно сходящегося ряда
- •2. Интегрирование и дифференцирование
- •§4. Степенные ряды
- •1.Степенной ряд и область его сходимости
- •2. Нахождение радиуса сходимости степенного ряда
- •3. Равномерная сходимость степенного ряда
- •4. Непрерывность суммы степенного ряда
- •5. Интегрирование и дифференцирование степенных рядов
- •§5. Ряд Тейлора
- •1. Бесконечная дифференцируемость суммы степенного ряда
- •2. Разложение функции в степенной ряд. Ряд Тейлора
- •3. Разложение элементарных функций в ряд Тейлора
3. Равномерная сходимость степенного ряда
Теорема 3.
Степенной ряд (1) 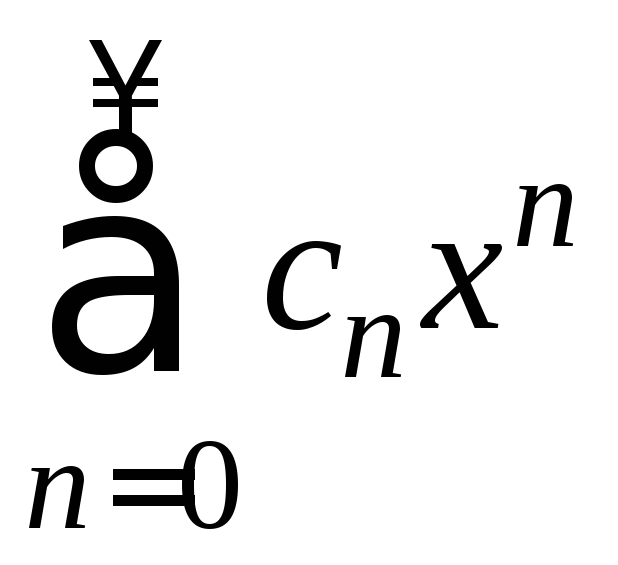 с радиусом сходимости
с радиусом сходимости
![]() сходится равномерно и абсолютно на
любом отрезке
сходится равномерно и абсолютно на
любом отрезке![]() принадлежащем интервалу сходимости
принадлежащем интервалу сходимости![]() ряда (1).
ряда (1).
Доказательство.
![]()
 Рассмотрим
произвольный отрезок
Рассмотрим
произвольный отрезок
![]() Ясно, что
Ясно, что![]() Обозначим через
Обозначим через![]() Тогда
Тогда![]() То есть
То есть![]() выполнено неравенство
выполнено неравенство![]() Так как
Так как![]() то в точке
то в точке![]() ряд (1) сходится абсолютно, то есть
сходится числовой ряд
ряд (1) сходится абсолютно, то есть
сходится числовой ряд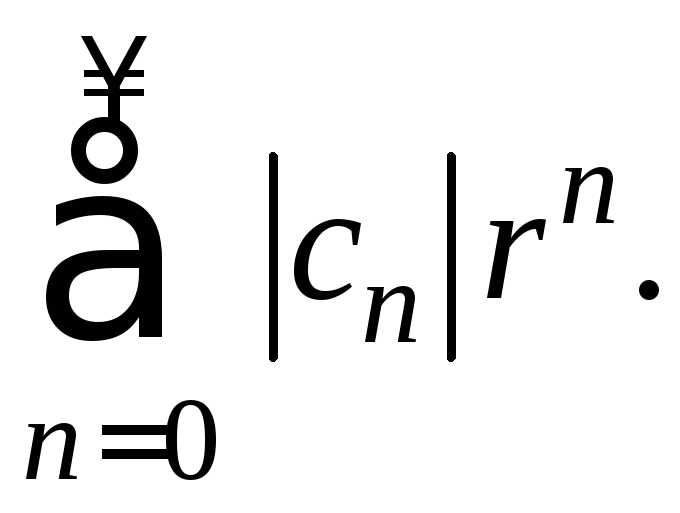 Так как
Так как![]() на отрезке
на отрезке![]() то
то![]()
![]()
![]() .
Тогда по признаку Вейерштрасса ряд (1)
сходится на
.
Тогда по признаку Вейерштрасса ряд (1)
сходится на![]() абсолютно и равномерно.
абсолютно и равномерно.![]()
4. Непрерывность суммы степенного ряда
Теорема 4.
Сумма степенного ряда (1) 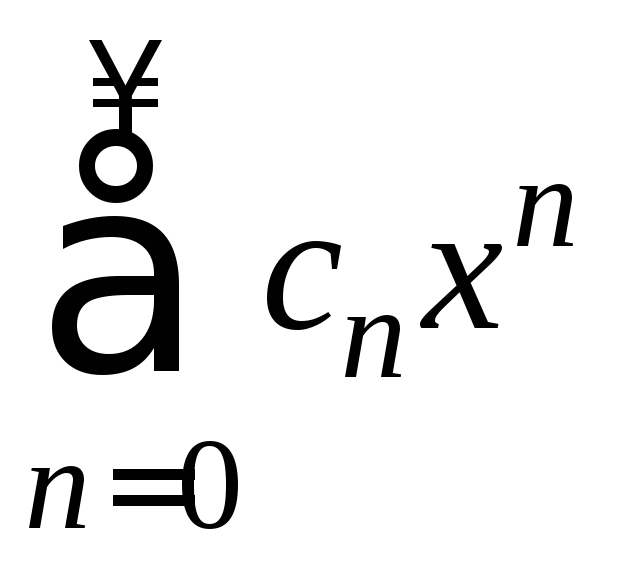 непрерывна во всех
точках интервала сходимости
непрерывна во всех
точках интервала сходимости
![]() .
.
Доказательство.
![]() Выберем произвольную
точку из интервала сходимости (х0:
Выберем произвольную
точку из интервала сходимости (х0:![]() ).
Докажем, что сумма ряда (1) непрерывна в
точкех0.
).
Докажем, что сумма ряда (1) непрерывна в
точкех0.
Можно подобрать
число
![]() так, чтобы
так, чтобы![]() ,
то есть
,
то есть![]() .
Так как
.
Так как![]() ,
то по теореме 3 ряд (1) равномерно сходится
на
,
то по теореме 3 ряд (1) равномерно сходится
на![]() .
Члены ряда (1) являются непрерывными
функциями на
.
Члены ряда (1) являются непрерывными
функциями на![]() .
Следовательно, выполнены условия теоремы
о непрерывности суммы равномерно
сходящегося ряда (теорема 2 §3). Значит,
сумма ряда (1) непрерывна на отрезке
.
Следовательно, выполнены условия теоремы
о непрерывности суммы равномерно
сходящегося ряда (теорема 2 §3). Значит,
сумма ряда (1) непрерывна на отрезке![]() .
Поэтому, она непрерывна в любой внутренней
точке этого интервала. Следовательно,
непрерывна и в точкех0.
Так как х0
- произвольная точка из этого интервала
сходимости, то теорема доказана.
.
Поэтому, она непрерывна в любой внутренней
точке этого интервала. Следовательно,
непрерывна и в точкех0.
Так как х0
- произвольная точка из этого интервала
сходимости, то теорема доказана.
![]()
5. Интегрирование и дифференцирование степенных рядов
Теорема 5.
Степенной ряд (1) с
![]() можно почленно интегрировать по любому
отрезку, принадлежащему
можно почленно интегрировать по любому
отрезку, принадлежащему![]() .
.
Доказательство.
![]() Возьмём произвольный
отрезок
Возьмём произвольный
отрезок
![]() По теореме 3 ряд (1) равномерно сходится
на отрезке
По теореме 3 ряд (1) равномерно сходится
на отрезке![]() .
Функции
.
Функции![]() непрерывны на
непрерывны на![]()
![]() .
Следовательно, ряд (1) можно почленно
интегрировать на отрезке
.
Следовательно, ряд (1) можно почленно
интегрировать на отрезке![]() (теорема 4 §3.).
(теорема 4 §3.).
![]()
Замечание.
Если степенной ряд (1) почленно
проинтегрировать по какому – либо
фиксированному промежутку
![]() ,
то получим числовой ряд:
,
то получим числовой ряд:
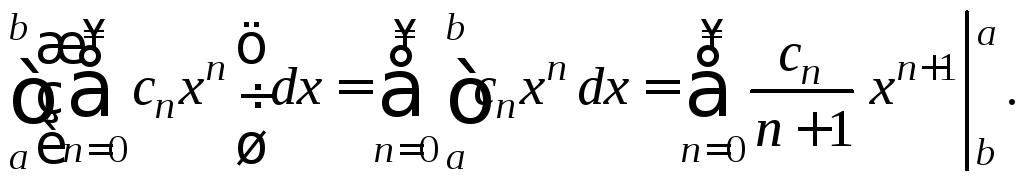
(определенный
интеграл по отрезку
![]() - это число).
- это число).
Иногда представляет
интерес интегрировать по отрезку с
фиксированным началом и переменным
концом. Например, по [0;x],
где |x|<R.
Тогда х:
![]() выполнено
выполнено![]() .
Следовательно,
.
Следовательно,
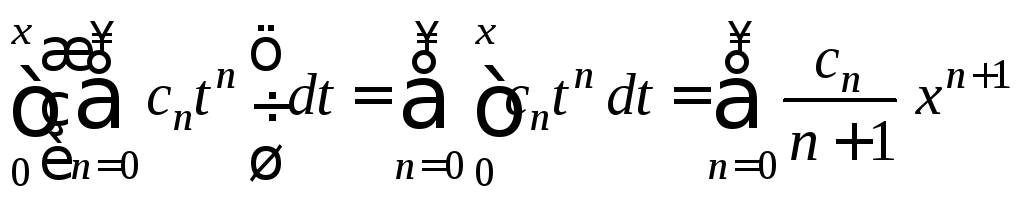 . (4)
. (4)
Ряд (4)
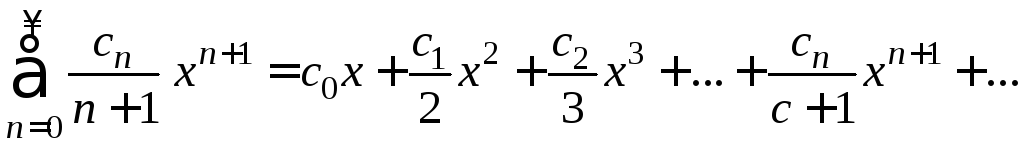 тоже является степенным. Его сумма равна
интегралу от суммы
тоже является степенным. Его сумма равна
интегралу от суммы![]() ряда (1). Так как
ряда (1). Так как![]() непрерывна на интервале
непрерывна на интервале![]() ,
то существует
,
то существует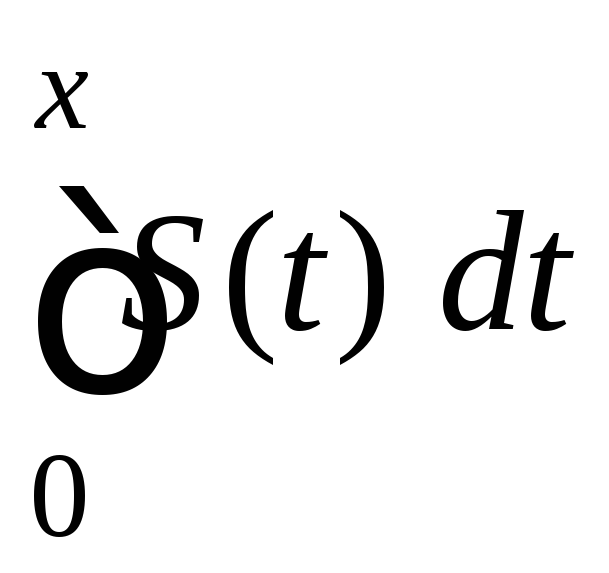 на
на![]() ,
то есть существует сумма ряда (4)х:
,
то есть существует сумма ряда (4)х:
![]() .
Значит, ряд (4) сходитсях:
.
Значит, ряд (4) сходитсях:
![]() .
.
Рассмотрим теперь ряд, составленный из производных ряда (1).
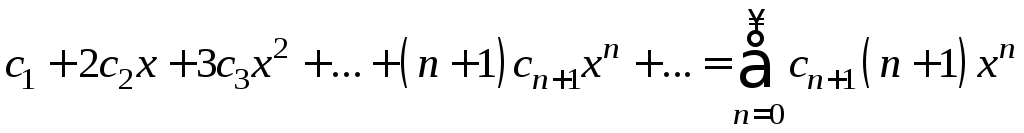 . (5)
. (5)
Теорема 6.
Степенной ряд (1) с
![]() можно почленно дифференцировать в любой
точке
можно почленно дифференцировать в любой
точке![]() из интервала сходимости.
из интервала сходимости.
Доказательство.
![]() Докажем, что ряд
(5) сходится в
Докажем, что ряд
(5) сходится в ![]() и что
и что
 ,
где
,
где
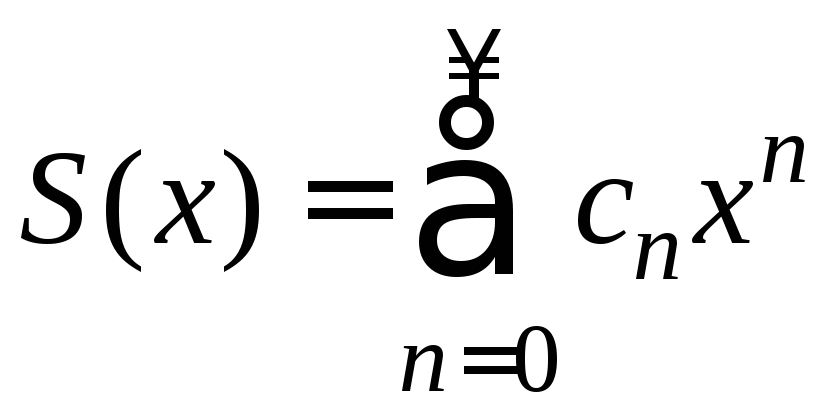 . (6)
. (6)
Возьмём
![]() .
Для того чтобы доказать соотношение
(6) будем пользоваться теоремой 6 из §3 о
почленном дифференцировании функционального
ряда. Докажем возможность её применения.
.
Для того чтобы доказать соотношение
(6) будем пользоваться теоремой 6 из §3 о
почленном дифференцировании функционального
ряда. Докажем возможность её применения.
члены ряда (1) непрерывно дифференцируемы на
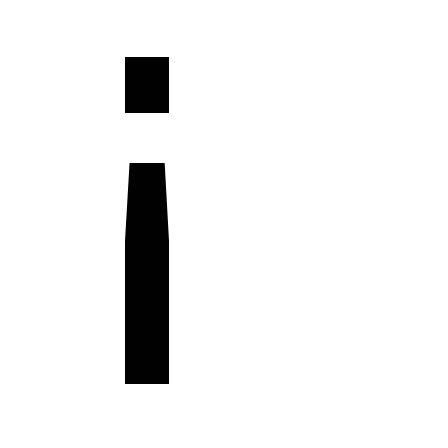 ;
;ряд (1) сходится абсолютно на
 ,
поэтому он сходится
,
поэтому он сходится .
.
Проверим выполнение третьего условия теоремы.
По взятому х0
подберём два положительных числа r1
и r2
так, чтобы
![]() .
Покажем, что ряд (5) равномерно сходится
на отрезке
.
Покажем, что ряд (5) равномерно сходится
на отрезке![]() .
Так как значение
.
Так как значение![]() входит в интервал сходимости
входит в интервал сходимости![]() ,
то ряд (1) абсолютно сходится в точке
,
то ряд (1) абсолютно сходится в точке![]() .
То есть сходится ряд
.
То есть сходится ряд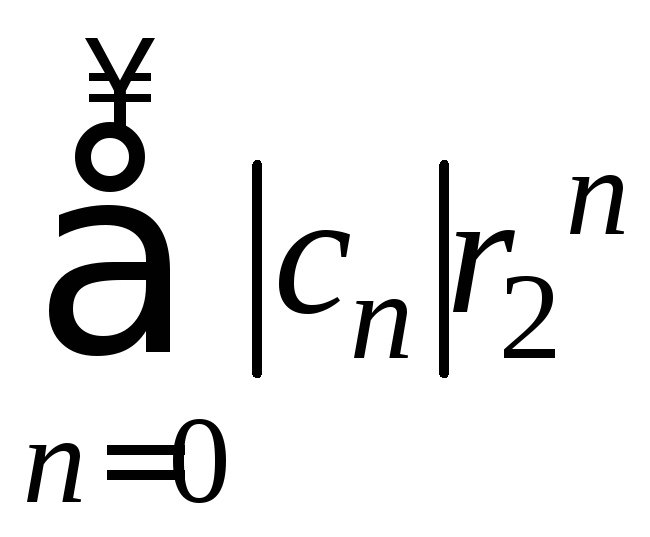 .
Тогда по необходимому условию сходимости:
.
Тогда по необходимому условию сходимости:![]() .
Следовательно, последовательность
.
Следовательно, последовательность![]() ограничена, то есть
ограничена, то есть![]() :
:![]() выполнено неравенство
выполнено неравенство![]() .
.
Оценим общий член
ряда (5) для
![]() :
:
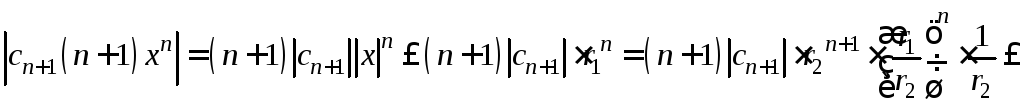
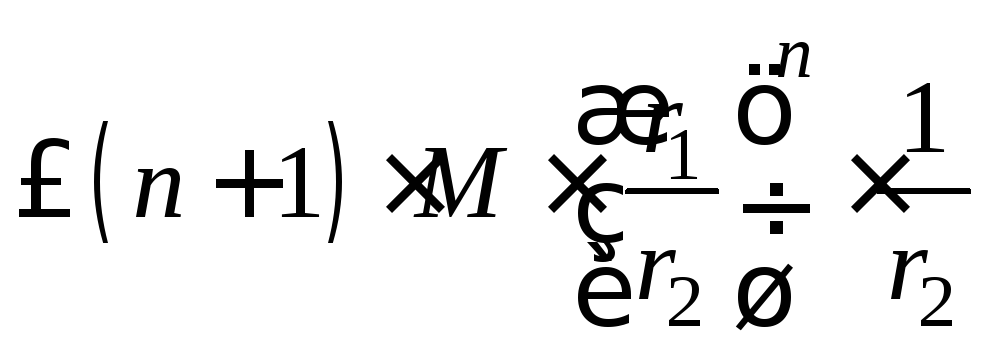 .
.
Обозначим
через
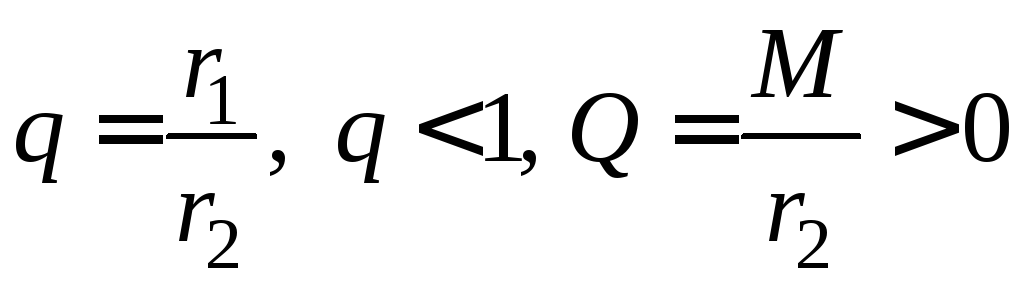 .
Тогда
.
Тогда![]()
![]() :
:![]() выполнено
выполнено
![]() . (7)
. (7)
Рассмотрим ряд
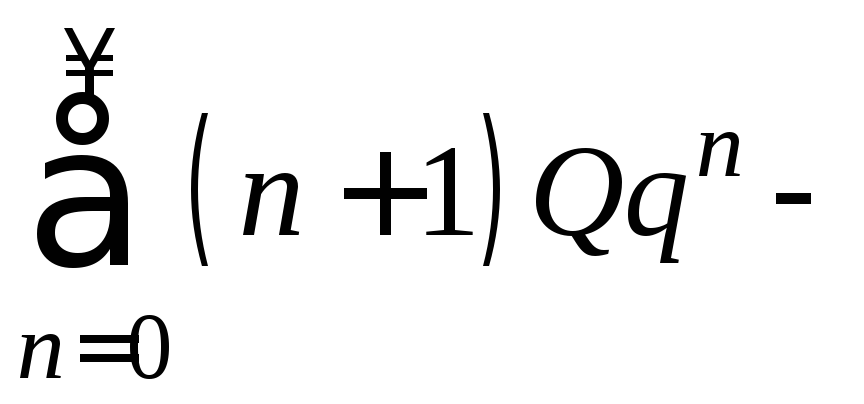 положительный ряд. По признаку Даламбера
положительный ряд. По признаку Даламбера
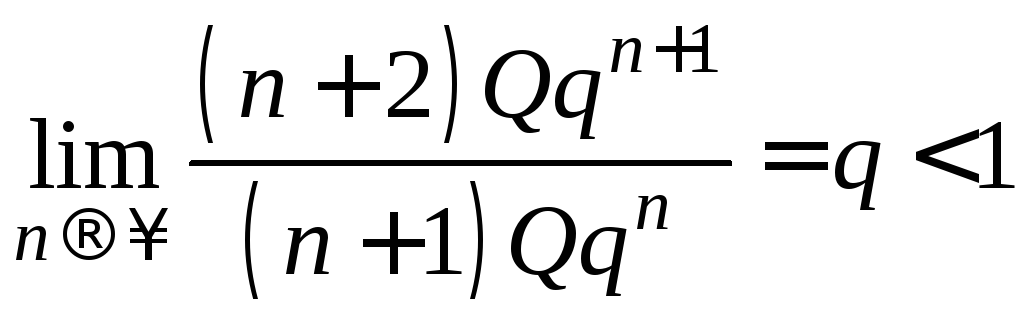 ,
значит, ряд сходится. Тогда из неравенства
(7) по признаку Вейерштрасса следует
абсолютная и равномерная сходимость
ряда (5) на отрезке
,
значит, ряд сходится. Тогда из неравенства
(7) по признаку Вейерштрасса следует
абсолютная и равномерная сходимость
ряда (5) на отрезке
![]() .
.
Итак, для ряда (1)
выполнены все условия теоремы 6 §3 о
дифференцировании функционального
ряда. Следовательно, ряд (1) можно почленно
дифференцировать ![]() и
и
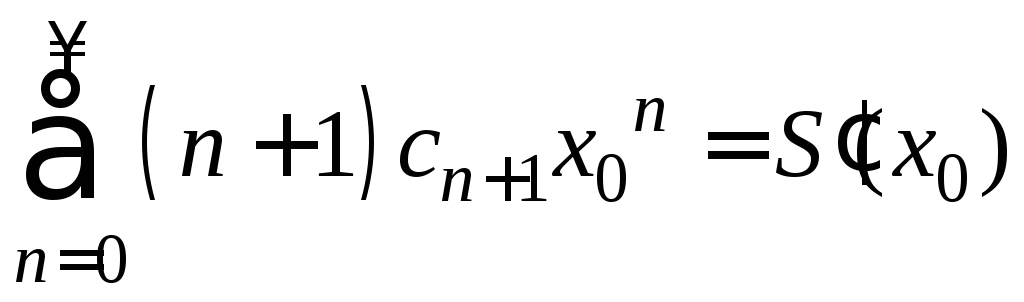 .
.
Так как х0
- произвольная точка из
![]() ,
то ряд (1) можно почленно дифференцировать
на
,
то ряд (1) можно почленно дифференцировать
на![]() .
Дифференцируя, получим:
.
Дифференцируя, получим:

![]()
Остаётся выяснить вопрос о том, каковы радиусы сходимости рядов (4) и (5).
Теорема 7. Радиусы сходимости рядов, полученных из степенного ряда (1) почленным интегрированием или дифференцированием совпадают с радиусом сходимости исходного ряда.
Доказательство.
![]() Пусть
Пусть
![]() соответственно
радиусы сходимости рядов (1), (4) и (5). Из
теорем 5 и 6 следует, что ряды (4) и (5)
сходятся на
соответственно
радиусы сходимости рядов (1), (4) и (5). Из
теорем 5 и 6 следует, что ряды (4) и (5)
сходятся на![]() и их суммы соответственно равны:
и их суммы соответственно равны:
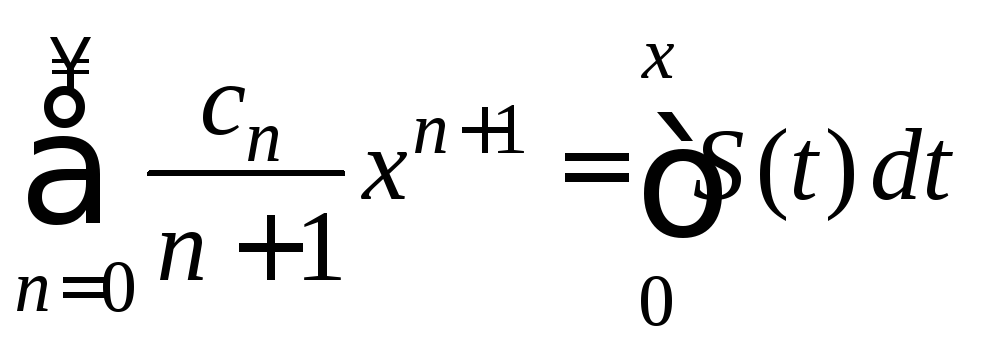 ,
,
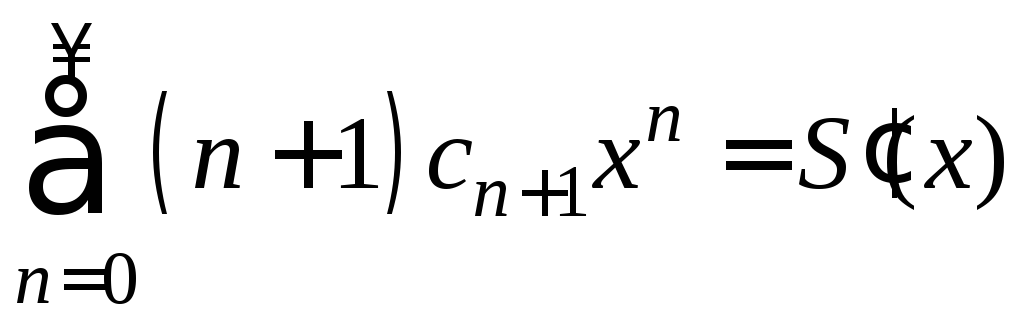 ,
где
,
где .
.
То есть почленное
интегрирование, и дифференцирование
степенного ряда не уменьшает его радиуса
сходимости:
![]()
Но ряд (1) можно
получить почленным дифференцированием
ряда (4), значит,
![]() ,
или почленным интегрированием ряда (5)
и, поэтому,
,
или почленным интегрированием ряда (5)
и, поэтому,![]() .
.
Следовательно,
![]() .
.![]()
Пример 1. Найти сумму степенного ряда
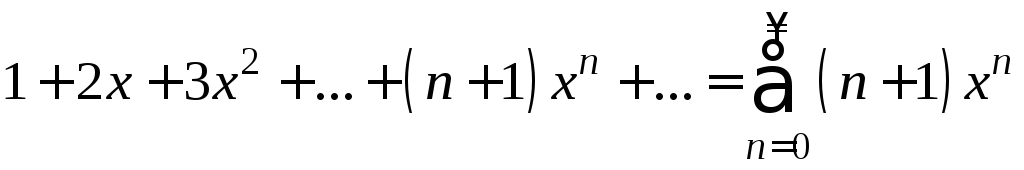 . (*)
. (*)
![]()
Δ Легко заметить,
что члены ряда, являются производными
от
![]() ,
,![]() .
Поэтому, рассмотрим ряд
.
Поэтому, рассмотрим ряд![]() . (**)
(геометрический ряд с первым членом 1 и
знаменателем
. (**)
(геометрический ряд с первым членом 1 и
знаменателем![]() ).
Геометрический ряд сходится только при
).
Геометрический ряд сходится только при![]() .
Поэтому, радиус сходимости ряда
.
Поэтому, радиус сходимости ряда![]() равен 1.
равен 1.
Продифференцируем
ряд
![]() :
:
 ;
;
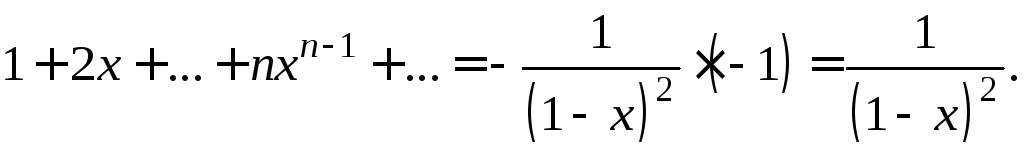
Итак, сумма ряда
![]() равна
равна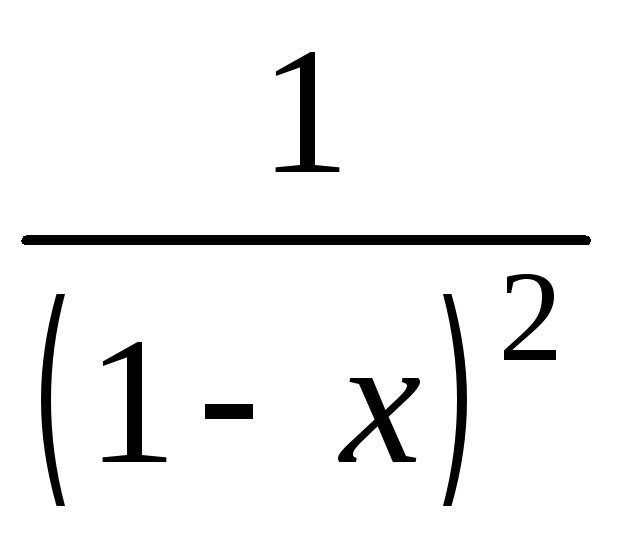 ,
радиус сходимости его тоже равен 1. Δ
,
радиус сходимости его тоже равен 1. Δ
Пример 2. Найти сумму степенного ряда
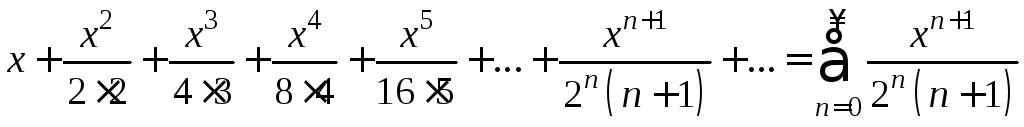 . (*)
. (*)
Δ Заметим, что в
знаменателе каждого члена ряда есть
множитель, совпадающий с показателем
степени у
![]() .
Значит, ряд
.
Значит, ряд![]() может быть получен интегрированием
какого – либо ряда (т.к.
может быть получен интегрированием
какого – либо ряда (т.к.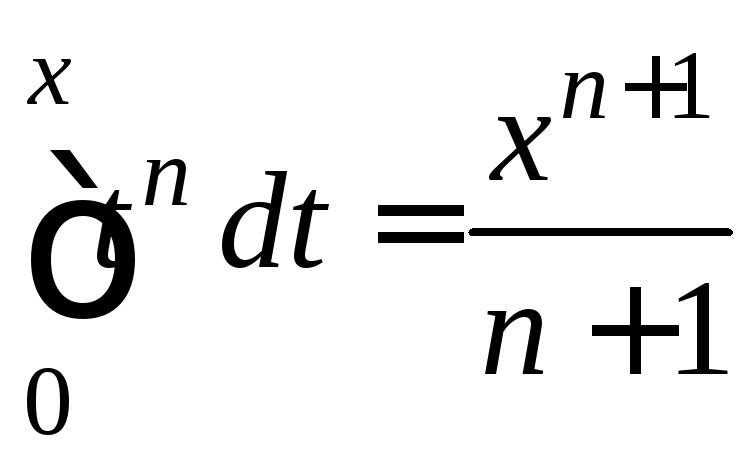 ).
Очевидно, это был ряд
).
Очевидно, это был ряд
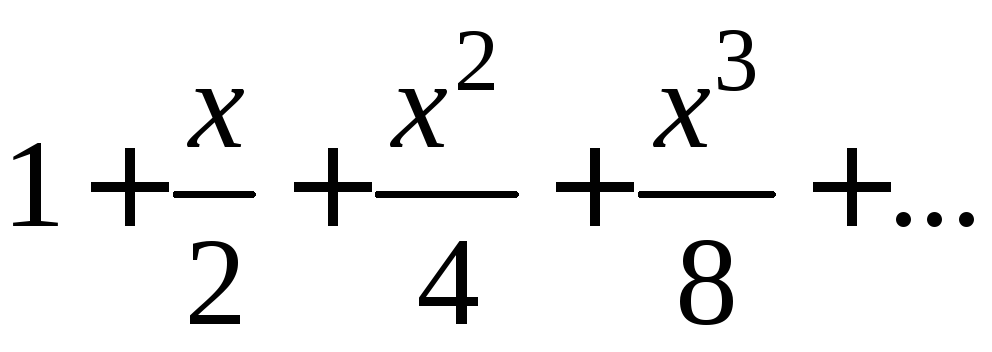
Этот ряд является
суммой геометрической прогрессии с
первым членом 1 и знаменателем
![]() .
Он абсолютно сходится при
.
Он абсолютно сходится при![]()
|x|<2
и
|x|<2
и
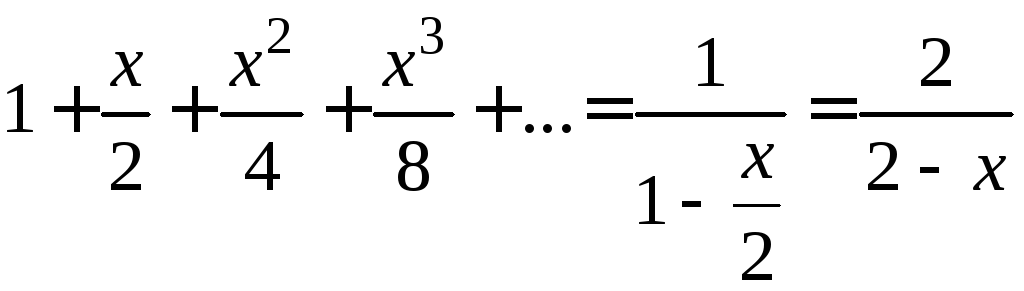 . (**)
. (**)
Поэтому, радиус
сходимости ряда
![]()
![]() .
.
Проинтегрируем
почленно
![]() на отрезке
на отрезке![]() ,
где
,
где![]() :
:
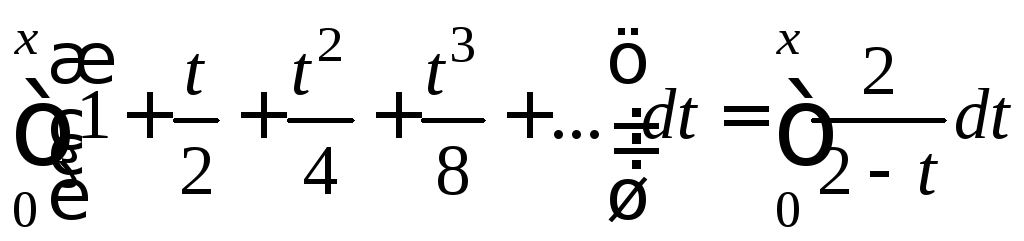 ;
;

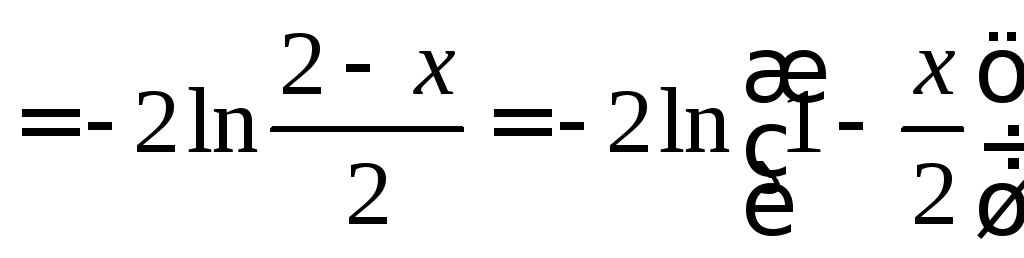 .
.
Итак, радиус
сходимости ряда
![]()
![]() и его сумма равна
и его сумма равна .Δ
.Δ
