6. Обработка результатов измерений

6.1. Определить требуемые величины и заполнить соответствующие графы таблиц 1. и 2, сделав необходимые расчеты по формулам:

.

Здесь P₂иηмощность нагрузки и КПД соответственно.

6.2. Проверить результаты измерений, для чего сравнить значения коэффициентов A,B,CиDтабл. 1. и 2 (значения соответствующих коэффициентов должны совпадать), кроме того, должно соблюдаться соотношениеA D-BС=1.

6.3. По табл. 1 построить графики зависимостей I₁(I₂),U₂(I₂),P₁(I₂),P₂(I₂) иη(I₂), сделать анализ построенных зависимостей.

Лабораторная работа №8 Исследование линейных электрических цепей при несинусоидальном входном напряжении

1. Цель работы

Исследование влияния реактивных элементов на форму кривых несинусоидального напряжения и тока.

2. Краткие теоретические сведения

Периодическими несинусоидальными токами и напряжениями называют токи и напряжения, измеряющиеся во времени по периодическому несинусоидальному закону.

Они возникают при следующих режимах работы электрической цепи (и при сочетании этих режимов):

1) источник Э.Д.С (источник тока) дает несинусоидальную Э.Д.С (ток), а все элементы цепи линейные;

2) источник Э.Д.С (источник тока) дает синусоидальную Э.Д.С (ток), но один или несколько элементов цепи нелинейные;

3) источник Э.Д.С (источник тока) дает несинусоидальную Э.Д.С (ток) и цепь содержит один или несколько нелинейных элементов;

4) источник Э.Д.С (тока) дает постоянную или синусоидальную Э.Д.С, а один или несколько элементов цепи периодически изменяются во времени.

При расчете электрических цепей с несинусоидальными Э.Д.С используют разложение несинусоидальных функций в тригонометрический ряд Фурье.

Из курса математики известно, что любую непрерывную периодическую функцию, удовлетворяющую условию Дирихле (т.е. получающую через равные промежутки времени те же значения), можно разложить в ряд Фурье. Существует две формы записи ряда Фурье:

(1)

(2)

где A₀– постоянная составляющая;

A_1msin(ωt+ψ₁)- первая (основная) гармоника, частота которой равна частоте несинусоидальной функции;

A_2msin(2ωt+ψ₂), …A_kmsin(kωt+ψ_k)- высшие гармоники;

A_km– амплитудаk-гармоники;

ψ_k- начальная фазаk-гармоники.

Связь между двумя формами записи ряда Фурье устанавливается по формулам:

(3)

Наличие тех или иных гармоник в ряде Фурье зависит от вида симметрии несинусоидального сигнала.

Разложить в ряд Фурье несинусоидальную функцию можно, используя аналитический или графоаналитический методы.

Если функция задана аналитически, то постоянную составляющую A₀и амплитуды значения гармоникB_kmиC_kmопределяют по формулам:

(4)

(5)

(6)

Графоаналитический метод применяют, если несинусоидальная функция задана в виде графика. Этот метод основан на замене определенного интеграла суммой конечного числа слагаемых. Для этого период функции разбивают на n равных частей, определяют значение функции в середине каждого интервала и рассчитывают коэффициенты ряда Фурье по приближенным формулам:

(7)

(8)

(9)

где р– текущий индекс, принимающий значение от 1 до n;

f_p(n)– значение функции в серединеринтервала;

x = (p-0,5) 2π/n - значение угла в серединеринтервала;

k– номер гармоники.

Рассмотрим графоаналитический метод определения коэффициентов ряда Фурье на примере.

Пример.

Разложить в ряд Фурье несинусоидальное напряжение, представленное на рис. 1.

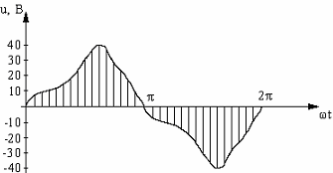
Рис. 1

Таблица 1

р	1	2	3	4	5	6	7	8	9	10	11	12
up(ωt),В	2,5	8	10	12,5	17,5	25	35	40	33	25	15	3,5
x = (p-0,5) 2π/n	7,5	22,5	37,5	52,5	67,5	82,5	97,5	112,5	127,5	142,5	157,5	172,5

р	13	14	15	16	17	18	19	20	21	22	23	24
up(ωt),В	-2,5	-8	-10	-12,5	-17,5	-25	-35	-40	-33	-25	-15	-3,5
x=(p-0,5)2π/n	187,5	202,5	217,5	232,5	247,5	262,5	277,5	292,5	307,5	322,5	337,5	352,5

Заданная функция симметрична относительно оси абсцисс, поэтому тригонометрический ряд Фурье будет состоять только из нечетных гармоник. Используя графоаналитический метод, разложим заданное напряжение в ряд Фурье, ограничившись первой и третьей гармониками.

Разбиваем период заданной функции на 24 равных интервала (значения коэффициентов ряда Фурье будет тем точнее, чем больше n, обычноn=24). По графикуu(ωt)определяем значения напряжения в середине каждого интервала и найденные значения записываем в таблицу 1. В этой же таблице приведены значения углов для каждого участка, рассчитанные по формуле

x = (p-0,5) 2π / n

Например, для второго интервала

x = (2-0,5) 2π / 24=22,5°.

Используя формулы (8) и (9), определяем коэффициенты ряда Фурье.

Обычно реализация формул (7), (8) и (9) осуществляется на ЭВМ.

Результаты вычислений:

u(ωt)=30,7 sin (ωt-13,1)+ 7,64 sin (3ωt-84,8)

Разложение в ряд Фурье наиболее часто встречающихся в электротехнике периодических сигналов (сигналы треугольной, прямоугольной, трапецеидальной форм и т.п.) приведены в справочниках, например, по математике, ТОЭ.

При анализе электрических цепей с несинусоидальными токами и напряжениями используют действующее и среднее значения несинусоидальной функции.

Действующее значение тока (напряжения) – это среднеквадратичное значение за период.

. (10)

Подставив в формулу (10) выражение тока, представленного рядом Фурье i=I₀+I_1m sin (ωt+ψ₁) +I_2m sin (2ωt+ψ₂)+ … , и выполнив необходимые математические операции, имеем

, (11)

где I_k = I_km / - действующее значениеk-гармоники.

Таким образом, действующее значение несинусоидального тока или напряжения равно корню квадратному из суммы квадратов постоянной составляющей и действующих значений отдельных гармоник. Для напряжения формула имеет вид:

(12)

Под средним по модулю значением функции понимают среднее значение модуля этой функции за период

. (13)

Измерения несинусоидальных токов и напряжений можно осуществлять приборами различных систем. При этом следует помнить, что приборы электромагнитной , электродинамическойсистем измеряют действующее значение; магнитоэлектрические приборы с выпрямителем- на среднее по модулю значение величины.

Для характеристики формы периодических несинусоидальных сигналов используют коэффициенты амплитуды, формы, искажения.

Коэффициент амплитуды – это отношение максимального значения функции к её действующему значению:

(14)

Коэффициент формы – это отношение действующего значения несинусоидальной функции к её среднему по модулю значению:

(15)

В электрических цепях при несинусоидальных токах и напряжениях, представленных рядом Фурье, активная, реактивная и полная мощности определяются по следующим формулам:

, (16)

, (17)

S=UI, (18)

где U_k , I_k– действующие значения гармоник напряжения и тока;

U, I– действующие значения несинусоидального напряжения и тока;

φ_k=ψ_ku-ψ_ki– угол сдвига фаз между напряжением и токомk-гармоники.

Мощность искажения

. (19)

Расчет электрических цепей при несинусоидальном входном напряжении проводят в следующем порядке:

1. Несинусоидальное входное напряжение (или Э.Д.С) раскладывают в тригонометрический ряд Фурье.

2. Используя метод наложения и комплексный метод расчета, для каждой гармоники входного напряжения определяют частичные токи (или напряжения).

3. Мгновенное значение требуемого тока (или напряжения) получается в виде ряда Фурье, членами которого являются частичные токи (или напряжения), найденные в пункте 2.

При расчете электрических цепей при несинусоидальных токах и напряжениях следует учитывать, что сопротивления реактивных элементов зависят от частоты.

Сопротивление индуктивного элемента растет прямо пропорционально частоте, поэтому для k-гармоникиX_Lkвkраз больше, чем для первой гармоники:

X_L1= ω L,

X_{L k}= k ω L= k X_L1. (20)

Сопротивление емкостного элемента уменьшается с ростом частоты, поэтому для k-гармоникиX_ckвkраз меньше, чем для первой гармоникиX_c1:

,. (21)

Для постоянной составляющей несинусоидального напряжения (или Э.Д.С) сопротивления индуктивного и емкостного элементов равны:

X_L= ω L = 0, X_С= 1 / ω С = ∞ . (22)