Готовимся к экзамену по матану стр. 8www.fakultet.net

Готовимся к экзамену по матану

1. Основные теоремы дифф. Исчисления: Теорема Ферма (необходимое условие экстремума для гладких функций).

Пусть f(x) функция, заданная на закрытом интервале [ a, b ], дифференцируемая на открытом (a, b) такая что в точке С выполнено: является точкой экстремума, т.е. точкой максимума или минимума. Тогда в точке С производная равна нулю.

Док-во: Пусть С — точка максимума, т.е. аналогично С точка минимума, т.е., тогда. Оценимпри х > С и0 при. Тогда, переходя к пределу, при х→С получим, а это возможно только еслиf''(C) = 0. Замечание: Теорему Ферма можно рассматривать как теорему о необходимых условиях экстремума функции на открытом интервале.

2. О.Т.Д.И.: теорема Ролля. (Мишель Ролль — фр. Математик (1652–1719))

Пусть функция f(x) непрерывна на сегменте [ a, b] и дифференцируема во всех внутренних точках этого сегмента. Пусть, кроме того, . Тогда внутри сегмента [a, b ] найдется точка С такая, что значение производной в этой точке равно нулю. (короче: между двумя равными значениями дифференцируемой функции обязательно лежит нуль производной этой функции).

Доказательство: Т.к. функция f(x) непрерывна на сегменте [ a, b ], то, по теореме Вейерштрасса №2 эта функция достигает на этом сегменте своего максимального значения М и своего минимального значения m. Могут представиться два случая: 1) M = m, 2) M > m. В случае 1) f(x) = M = m = const. Поэтому производная равна нулю в любой точке сегмента а б. В случаеM > m, поскольку , можно утверждать, что хотя бы одно из двух значений М илиm достигается функцией в некоторой внутренней точке С сегмента [ a, b ]. Но тогда функция f(x) имеет в этой точке С локальный экстремум. Поскольку функция f(x) дифференцируема в точке С, то по теореме Ферма . Теорема доказана.

3. О.Т.Д.И.: теорема Лагранжа. (:Жозеф Луи Лагранж — великий фр. Математик и механик (1736–1813)).

Если функция f(x) непрерывна на [ a, b ] и дифференцируема во всех внутренних точках этого сегмента, то внутри сегмента [ a, b ] найдется точка С такая, что справедлива формула: . Эту формулу называют формулой Лагранжа и формулой конечных приращений.

Д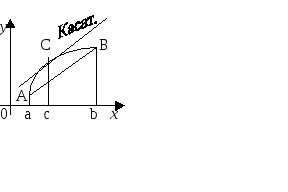оказательство: Рассмотрим на сегменте [ a, b ] следующую вспомогательную функцию:(1). Проверим, что для функцииF(x) выполнены все условия теоремы Ролля. В самом деле, F(x) непрерывна на сегменте [ a, b ] (как разность функции f(x) и линейной функции) и во всех внутренних точках сегмента [ a, b ] имеет производную, равную . Из формулы (1) очевидно, что(2). Из равенства (2) вытекает формула Лагранжа. Замечание: теорема Ролля является частным случаем теоремы Лагранжа. Геометрический смысл: На кривойу = f(x) между точками А и В найдется такая точка С, касательная к которой параллельна секущей АВ.

4. О.Т.Д.И.: теорема Коши-Лагранжа. (обобщение теоремы Лагранжа). (Огюстен Луи Коши — фр. Математик (1789–1857) хорошо, что умер, а то убила бы!)

Пусть f(x) и g(x) заданы, непрерывны на [ a, b ] и дифференцируемы на ( a, b ) и g(x) не обращается в ноль для любых х из ( a, b ), /оно и не может быть равным /, внутри [ a, b ], тогда существует точка С, причем: .

Доказательство: Рассмотрим вспомогательную функцию: . в силу требований, наложенных на функции f(x) иg(x), функция F(x) непрерывна на сегменте [ a, b ] и дифференцируема во всех внутренних точках этого сегмента. Кроме того, F(a) = F (b) = 0. Таким образом, для F(x) выполнены все условия теоремы Ролля. Согласно этой теореме внутри сегмента [ a, b ] найдется точка С такая, что . Имея в виду, чтои используя т. Ролля будем иметь:. Учитывая, чтоиз этого равенства получим формулу Коши. Теорема доказана.