9. Общий план исследования функций. Теорема о достаточных условиях монотонности функции на интервале.

1)Если f(x) дифференцируема на ( a, b ) и ее производная больше (больше либо равна) нуля, то f(x) строго возрастает (не убывает) на интервале ( a, b ) 2) Если f(x) дифференцируема на ( a, b ) и ее производная меньше (меньше либо равна) нуля, то f(x) строго убывает (не возрастает) на ( a, b ).

Доказательство: Пусть , тогда по теореме Лагранжа. Для пункта 2 аналогично.

10. О.П.И.Ф.: Экстремумы функции. Теоремы о необходимом (формулировка) и достаточном условии экстремума дифференцируемой и непрерывной функции на интервале.

описание точек локальных экстремумов: Будем говорить, что точка — точка локального максимума (минимума), если существует некоторая окрестность точки, такая, что для любого х из нее будет следовать, что. Точки локальных максимумов и минимумов называются точками экстремума.

Теорема о необходимом условии экстремума: Если — точка экстремума функции f(x), диффференцируемой на ( a, b ) , тоДоказательство: применим теорему Ферма к интервалу, гдедля любого х принадлежащего, откуда следует, что. Замечание: это условие является необходимым, но не достаточным.

Теорема о достаточном условии экстремума функции: если функция f(x) непрерывна в точке и дифференцируема в некоторой окрестности этой точки (в проколотой окрестности), ии, т.е. производная в точкеменяет знак.

Доказательство: По теореме Лагранжа 1.

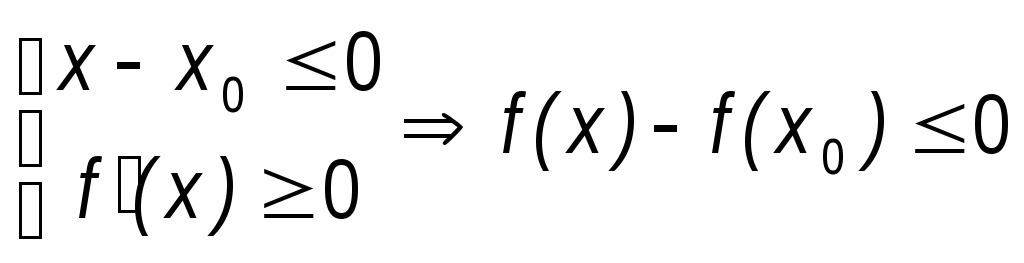
2. 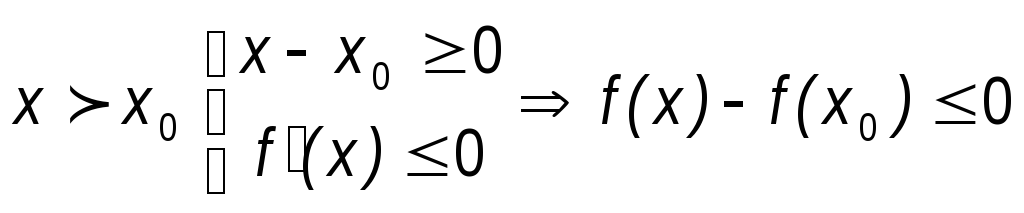. Из п.1 и п.2 следует, чтовсегда,, т.е.точка макс.

Опр.: критическими точками функции у=f(x) назовем точки, где производная равна нулю или не существует.

11. О.П.И.Ф.: Определение выпуклости вверх (вниз) функций. Теорема о достаточных условиях выпуклости вверх (вниз) дважды дифференцируемой функции.

График функции f(x) называется на интервале ( a, b ) выпуклым вверх (вниз) если график у=f(x) лежит ниже (выше) любой касательной, проведенной к графику в этом интервале. Опр.: точкой перегиба называется точка графика в которой график меняет направление выпуклости.

Теорема о дост. усл. выпуклости: если на ( a, b ), то график у=f(x) выпуклый вниз (вверх)

12. О.П.И.Ф.: Определение точки перегиба. Теорема о достаточных условиях существования точки перегиба.

Опр.: Точкой перегиба называется точка графика, в которой график меняет направление выпуклости.

Теор.: (необх. и дост. усл.) Пусть f(x) дважды дифференцируема на ( a, b ) и существует такая точка С — точка перегиба, тогда 2. Если вторая производная функции f(x), дифференцируемой на ( a, b ) кроме, может быть, самой точки С, в т.С меняет знак, то точка С — точка перегиба.

/не по делу/ Общий план исследования функций: 1) Определить область задания функции 2) Определить четность, нечетность, периодичность. 3) Определить нули функции и точки пересечения с 0у 4) исследовать точки разрыва 5) построить асимптоты 6) Исследовать участки монотонности 7) определить точки экстремума 8) определить направление выпуклости 9) определить точки перегиба 10) построить эскиз функции

13.О.П.И.Ф.: Определение асимптоты функции. Виды асимптот.

Опр.: асимптота — прямая, к которой график функции f(x) приближается сколь угодно близко, но не пересекает ее при стремлении х к или к точкам разрыва второго рода, когдаАсимптоты бывают: вертикальные, горизонтальные, наклонные.

1) Если существует точка С такая, что , то прямая х=С вертикальная асимптота функции.

2) Если существует, то прямая у=b — горизонтальная асимптота функции.

3) Если существует прямая , такая, что, то прямая— наклонная ассимптота.