32

«Розуміння і вміння застосовувати принцип математичної індукції

є добрим критерієм зрілості, яка цілковито необхідна математику»

А.М. Колмогоров

Вступ

Метод математичної індукції застосовується в найрізноманітніших областях математики і не тільки. Оскільки цей метод по суті пов’язаний з поняттям числа, то найчастіше він застосовується в арифметиці, алгебрі і теорії чисел. Проте поняття цілого числа є основним не тільки в цих розділах математики, а й, наприклад, в геометрії, тригонометрії. Зокрема, застосування цього методу в геометрії особливо цікаві і ефективні.

За індукцією не тільки зручно проводити доведення, а і давати деякі означення.

Наприклад. Нехай є деяка людина А. Її родичами першого порядку назвемо її батьків і дітей. Якщо визначені родичі k-го порядку, тоді родичами (k+1) порядку для А назвемо родичів першого порядку для родичів А k-го порядку, які не є родичами А меншого порядку. Наприклад, брати та сестри при такому означенні є родичами другого порядку.

Індуктивні визначення мають важливу роль у таких науках, як математична логіка і математична лінгвістика. Доведення за індукцією міцно ввійшли у математичну діяльність. Існує велика кількість модифікацій методу, орієнтованих на різні застосування.

Розглядають повну і неповну індукцію.

Метою курсової роботи є дослідження різних видів задач, які роз’язуються методом математичної індукції.

Об’єктом є задачі, які роз’язуються методом математичної індукції.

Предметом є аналіз і систематизація основних властивостей математичної індукції , на конкретних прикладах задач.

Структура курсової роботи. Курсова робота складається із вступу, дев’яти розділів, висновку і списку літератури, який складається із 12 джерел.

1. Повна індукція

Іноді зустрічаються задачі, в процесі розв’язування яких треба розглянути всі можливі випадки, тоді на основі цього можна зробити цілком обґрунтований висновок.

Якщо при доведенні теореми її поділяють на скінчене число тверджень і доводять кожне з них окремо, то такий метод доведення називається методом повної індукції.

Основою методу повної індукції є наступна аксіома логіки:

Якщо якусь властивість мають всі елементи множини А і всі елементи множини B і якщо 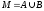, то цю саму властивість має і кожен елемент множини M.

Наведемо приклади доведень за допомогою методу повної індукції.

Приклад №1

У 1742 р. член Петербурзької Академії наук Х. Гольдбах у листі до Леонарда Ейлера висловив гіпотезу, що кожне парне число, більше від 2, можна подати як суму двох простих чисел. Ця гіпотеза досі не доведена і не спростована. Але, якщо обмежитись числами, меншими від певного числа, то таке твердження можна довести.

Доведення.

Доведемо, наприклад, що всяке парне число, яке задовольняє нерівність 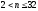, можна представити у вигляді суми двох простих чисел. Оскільки таких чисел скінчене число, то це твердження можна довести методом повної індукції, розглянувши всі можливі випадки:

4=2+2; 10=3+7; 16=5+11; 22=5+17; 28=5+23;

6=3+3; 12=5+7; 18=5+13; 24=7+17; 30=7+23;

8=3+5; 14=3+11; 20=3+17; 26=13+13; 32=29+3.

Твердження доведено.

Приклад №2

Довести, що коли n – довільне число, то серед трьох чисел n, n+10, n+14 обов’язково є число, яке ділиться на 3.

Доведення.

Зазначимо, що довільне число n або ділиться на 3, або дає при діленні на 3 остачу, що дорівнює 1 або 2.

n=3k або n=3k+1, або n=3k+2. Тому розглянемо відповідні три випадки:

1) n=3k, тобто 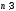, де k – натуральне число.

У цьому випадку твердження виконується – одне з чисел (число n) ділиться на 3;

2) n дає при діленні на 3 остачу 1, тобто n=3k+1.

Тоді 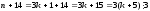, твердження виконується;

3) n дає при діленні на 3 остачу 2, тобто n=3k+2.

Тоді n+10=3k+2+10=3k+13=3(k+4)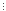3.

Отже, в усіх можливих випадках одне з даних чисел ділиться на 3 і тому твердження доведено.

Приклад №3

Довести, що при кожному цілому n число .

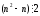Доведення.

n-n²=(n-1)n – це добуток двох послідовних цілих чисел. Одне з них обов’язково парне і ділиться на 2.

Кожне ціле число n при діленні на 2 дає остачу 0 або 1:

1) Якщо остача r=0, то n=2k, .

2) Якщо остача r=1, тоді n=2k+1

n-1=2k+1-1=2k. Отже, 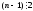. Інших випадків немає. Отже, яким би не було ціле число n, один із співмножників n, n-1, а тоді їх добуток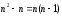ділиться на 2.

2. Неповна індукція

Інколи загальний висновок можна зробити після розгляду не всіх можливих випадків, а тільки деяких. Таке міркування не є строгим доведенням і називається неповною індукцією.

Результат, одержаний неповною індукцією, це гіпотеза, яка вимагає строгого доведення. Наведемо декілька прикладів.

Приклад №1

Знайти формулу для обчислення суми перших n натуральних чисел S(n)=1+2+3+4+5+…+n;

Розглянемо частинні випадки:

n=1 1=1,

n=2 1+2=3,

n=3 1+2+3=6,

n=4 1+2+3+4=10,

n=5 1+2+3+4+5=15.

Очевидно можна зробити припущення, що сума перших n членів натурального ряду S(n)=1+2+3+4+5+…+n=.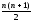

Доведемо цю гіпотезу одержану в результаті неповної індукції методом математичної індукції.

Доведення.

1. При n=1 , 1=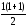=1. Рівність має місце.

2. Припустимо, що вона має місце і при n=k тобто S(k)=1+2+3+4+5+…+k=.

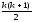Виходячи із цього припущення, доведемо, що воно істинне і для n=k+1 тобто, що S(k+1)=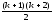. Запишемо S(k+1)=S(k)+(k+1).

Враховуючи припущення, маємо S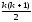(k+1)=+k+1==.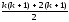

Робимо висновок, що формула вірна і при n= k+1.

Тоді за припущенням математичної індукції вона вірна і для будь-якого натурального n. S(n)=1+2+3+4+5+…+n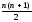.