3. Історична довідка. Метод математичної індукції

«Знання людей заслуговує ім’я Науки залежно

від того, яку роль має в ньому число»

Е. Борель

Принципом математичної індукції фактично користувалися ще деякі давньогрецькі вчені. Але вперше сформулював його у 1321р. французький філософ, математик, астроном Леві бен Гершону ( 1288-1344 ), більш відомий під прізвіщами Лев Герсонід, Ралбаг, метр Леон де Баньоль. Він жив у різних місцях Південної Франції.

Характеристика принципу математичної індукції є і у широко освідченого італійського математика XVIст. Ф. Мавроліко, перекладача Архімеда.

Метод доведень, що грунтується на принципі математичної індукції, називають методом математичної індукції. Доведення методом математичної індукції повинне складатися з двох самостійних теорем.

Теорема 1. Довести, що дане твердження справджується для n=1. Цю частину доведення називають базисом індукції – доведення істинності твердження А(1).

Теорема 2. Припустивши, що дане твердження правильне при n=k, де k-довільне натуральне число ( це припущення називають індуктивним припущенням ), доводимо, що твердження є правильним і для n=k+1. Ця частина доведення має назву індуктивний перехід або індуктивний крок.

Якщо обидва ці етапи проведено, то на підставі принципу математичної індукції твердження справедливе для всякого натурального n.

Дійсно, теорема 1 створює базу для проведення індукції, а теорема 2 дає право необмеженого автоматичного розширення цієї бази, право переходу від даного частинного випадку до дальшого.

Зауважуємо, що доведення методом математичної індукції безумовно вимагає доведення обох теорем 1 і 2, кожна з яких має своє особливе значення.

Спосіб доведення, який зараз називається методом математичної індукції, запропонували Блез Паскаль (1623-1663рр.) і Якоб Бернуллі (1654-1705рр.).

У “Трактаті про арифметичний трикутник ” Б. Паскаль доводить закон створення членів цього трикутника методом математичної індукції, після чого цей метод починає поступово притягувати увагу деяких вчених, окремо Я. Бернуллі.

Лише з другої половини XIXст. Після праць Больцано, Коші, Гауса, Абеля чисто індуктивні методи доведення утрачають значення у математиці. На перший план виходять дедукція і математична індукція.

Метод математичної індукції використовується і в експериментальних науках.

4. Неповна індукція і метод математичної індукції в прикладах і задачах на обчислення сум, добутків Приклад №1

Знайти формулу для обчислення суми S_n=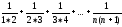Використаємонеповну індукцію. Розглянемо частинні випадки:

n=1 S₁=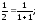

n=2 S₂=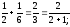

n=3 S₃=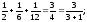

n=4 S₄=

n=5 S₅=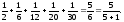

Можна зробити припущення, тобто виказати гіпотезу, що S_n=.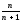

Доведемо цю формулу методом математичної індукції.

Доведення.

1) Базис індукції: При n=1 S₁=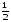=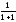формула вірна.

2) Індуктивний перехід:

Припустимо, що дана рівність має місце при n=k, тобто S_k=.()

Виходячи із цього припущення. Доведемо, що воно істине і для n=k+1, тобто, що S_k+1=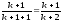, S_k+1= S_k+.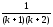

Враховуючи припущення () маємо: S_k+1==.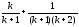

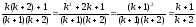Отже, формула вірна і при n=k+1. За принципом математичної індукції вона справджується і при будь-якому n.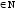

За допомогою методу неповної математичної індукції можна одержати і формули для добутків, а потім довести їх методом математичної індукції.