Приклад №2

Нехай 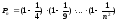де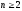

Із рівностей

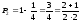; n=2

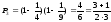; n=3

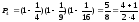; n=4. Робимо індукційний висновок, що .

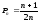Доведемо цю формулу

1 спосіб доведення.

1) При n=2 маємо 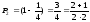. Формула вірна.

Припустимо, що при n=k, k>2 формула формула справджується, тобто.

Враховуючи це припущення, доведемо, що вона вірна і при n=k+1.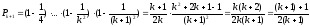

Формула справджується і при n=k+1.

Отже, за принципом повної математичної індукції, вона вірна і при ,

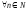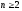
2 спосіб доведення.

При доведенні даної тотожності за допомогою методу математичної індукції корисно було б зробити так:

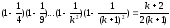Записати цю тотожність при n=k. (1), потім при n=k+1.(2)

Поділити (2) на (1), ліву частину на ліву, праву на праву.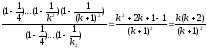

Одержали один і той самий вираз 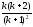, а це значить, що за методом математичної індукції можна сказати, що дана тотожність справджується при всіх натуральних n.

5. Узагальнення методу математичної індукції

В деяких задачах трапляється, що твердження, яке необхідно довести, має місце не для всіх натуральних значень n, а лише для значень n, починаючи з певного натурального числа n_о. У таких випадках можна скористатися узагальненим принципом математичної індукції.

Сформулюємо цей принцип:

Нехай твердження, що залежить від натурального числа n, задовольняє такі умови:

1. Це твердження є правильним при n=n_о;

2. З припущення правильності даного твердження при n=k (де kn_о) випливає його істинність і при n=k+1. Тоді дане твердження справджується при всіх натуральних nn_о.

Необхідно розуміти, що при значеннях n<n_о твердження може бути як вірним так і невірним; у всякому разі, яких-небудь заключень щодо істинності твердження при 1n < n_o з проведеного доведення методом математичної індукції зробити не можна.

Наведемо приклади використання узагальненого принципу математичної індукції.

Приклад №1

Довести, що 2ⁿ>2n+1, якщо

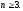
Доведення.

1) При n=3 маємо 2³>23+1, тому що 8>7. Вихідна нерівність правильна при n=3.

2) Припустимо, що нерівність вірна при n=k, тобто 2^k>2k+1.

Враховуючи це припущення, доведемо, що 2^k+1>2(k+1)+1 (при n=k+1).

Маємо 2^k+1=22^k>2(2k+1)=4k+2=2k+2+2k=2(k+1)+2k.

Оскільки 2k>1, то з останньої нерівності дістаємо 2^k+1>2(k+1)+1. А це означає, що нерівність правильна і при n=k+1.

Отже, за узагальненим принципом математичної індукції нерівність доведемо для всіх

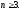
Зробимо зауваження, що при n ця нерівність не є правильною, так,

коли n=2, маємо: 2²<22+1,

4<5;

коли n=1, маємо 2<2+1,

2<3.

Тобто нерівність 2ⁿ>2n+1 неправильна при n=1; 2.

Наведемо ще один приклад, коли необхідно застосовувати узагальнений принцип математичної індукції. Розв’яжемо одну з комбінаторних задач.

Приклад №2

Довести, що будь-яку суму грошей, більшу 7 копійок, можна розміняти монетами тільки по 3 і 5 копійок.

Доведення.

Нехай сума дорівнює n копійок (n>7); nєN.

1) Якщо n=8, тоді наше твердження A(n) вірне: 8=3+5.

2) Припустимо, що твердження, яке ми позначили A(n), вірне і при n=k,

де k>8, kєN.

Існують два випадки розміну суми у k копійок монетами по 3 і 5 коп.:

а) тільки монетами по 3 коп. кожна;

б) виникає потреба хоча б однієї 5 коп. монети.

У випадку а) забираємо три монети по 3 коп., додаємо дві по 5 коп. і тим самим розмінюємо суму у (k+1) коп., тому що ми додамо до k суми одну копійку.

У випадку б) забираємо одну монету 5 коп.; додаємо дві монети по 3 коп. кожна і тим самим розмінюємо суму у (k+1) копійку. Задача розв’язана.