Приклад №4

Довести методом математичної індукції, що (m³+3m²+2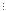m)6 для m.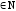

Доведення.

1)Базис індукції:

Переконаємося, що дане твердження має місце при n=1. M³+3m²+2m=1+3+2=6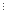6.

2)Індуктивний перехід:

Припустимо, що твердження має місце при m=k, тобто (k³+k²+2k)= k(k²+3k+2)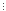6.

Виходячи з даного припущення доведемо, що дане твердження має місце і при n=k+1, тобто((k+1)³+3(k+1)²+2(k+1))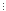6.

K³+3k²+3k+1+3k²+6k+3+2k+2=k³+6k²+11k+6=k³+2k+3k²+9k+6=

=(( k³+k²+2k)+3(k³+k²+2k))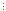6.

(k³+k²+2k) 6 за припущенням математичної індукції, кожен доданок суми ділиться на 6, тому і вся сума кратна 6.

Тоді за принципом математичної індукції число (m³+3m²+2m)6 для m.

Приклад №5

Довести методом математичної індукції, що число виду (7ⁿ⁺¹+8^2n-1) 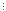19 при будь-якому натуральному n.

Доведення.

1)Базис індукції:

Переконаємося, що дане твердження має місце при n=1. 7²+8=57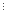19

2)Індуктивний перехід:

Припустимо, що твердження має місце при n=k, тобто (7^k+1+8^2k-1) 19.

Виходячи з даного припущення доведемо, що дане твердження має місце і при n=k+1.

7^k+1+1+8^2(k+1)-1=7^k+17+8^2k-18²=7^k+17+648^2k-1=77^k+1+78^2k-1+578^2k-1=

=7(7^k+1+8^2k-1)+578^2k-1.

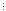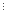Враховуючи припущення і те, що 5719, робимо висновок, що одержана сума ділиться на 19. Отже, твердження виконується і при n=k+1. Тоді за принципом математичної індукції число виду (7ⁿ⁺¹+8^2n-1) 19 при будь-якому натуральному n.

Приклад №6

Довести, що число (n³+5n) ділиться на 6, де n – довільне натуральне число.

Доведення.

1)Базис індукції:

при n=1 маємо 1+5=6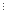6.

2)Індуктивний перехід:

Припустимо, що при n=k число ділиться на 6.

(k³+5k) 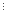6. Доведемо, що і при n=k+1 це число кратне 6.

(k+1)³+5(k+1)=k³+3k²+3k+1+5k+5=k³+5k+3k²+6=k³⁺5k+3k(k+1)+6.

3k(k+1) – цей добуток ділиться і на 3, і на 2 (одне з двох послідовних чисел: k або k+1 є число парне), тому він ділиться і на 6.

Отже, кожен доданок останньої суми ділиться на 6, тому вся сума кратна 6.

За принципом математичної індукції число виду (n³+5n) кратне 6.

Приклад №7

Довести, що для n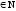число виду (11ⁿ⁺¹+12^2n-1) кратне 133.

Доведення.

1)Базис індукції:

Переконаємося, що при n=1 твердження справджується:

11¹⁺¹+12^2-1=121+12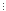=133133.

2)Індуктивний перехід:

Припустимо, що при n=k (11^k+1+12^2k-1)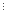133.

Виходячи з цього припущення, доведемо, що твердження справджується і при n=k+1.

11^k+1+1+12^2(k+1)-1=11^k+1 11+12²12^2k-1=11^k+111+14412^2k-1=

=11^k+111+1112^2k-1+13312^2k-1=11(11^k+1+12^2k-1)+13312^2k-1.

Кожен доданок одержаної суми ділиться на 133, тому і сума кратна 133.

Отже, при будь-якому натуральному n число (11ⁿ⁺¹+12^2n-1)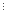133.

Часто метод математичної індукції використовують при доведенні деяких теорем або наслідків з них, в яких йде мова про натуральні числа. Наприклад при доведенні наслідку з теореми Безу.

Приклад №8

Довести, що різниця однакових степенів двох чисел завжди ділиться на різницю цих чисел, тобто при натуральному n .

Доведення.

1) При n=1 твердження вірно:

.

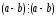2) Припустимо, що при n=k

.

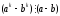Доведемо, що .

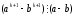До виразу 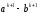додамо два вирази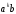і -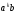. Одержимо

.

Перший доданок одержаної сум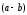и ділиться на , тому що другий ділиться на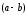за припущенням.

Отже, і вся сума тоді ділиться на

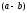
За припущенням математичної індукції 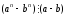при будь-якому n.

При доведенні деяких тверджень, які запропоновують на різних математичних олімпіадах, теж корисно застосовувати метод повної математичної індукції.