6. Деякі відомі визначні нерівності і метод математичної індукції Приклад №1.

Довести, що для будь-якого натурального n .

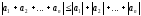Доведення.

1) При n=1 ;

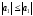n=2 .

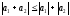Дійсно, a₁ і a₂ мають однакові знаки, або протилежні Якщо однакові, то , Якщо різні, то.

2) Припустимо, що нерівність вірна і для n=k доданків, тобто, що .

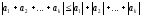Враховуючи це припущення, доведемо, що нерівність вірна і при n=k+1, тобто покажемо, що .

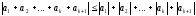Дійсно, .

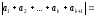
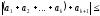
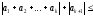
Отже, нерівність вірна і при n=k+1.

За принципом математичної індукції нерівність справджується для довільного натурального n.

Приклад 2

Довести нерівність Бернуллі 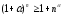, де,

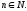
Доведення.

1) Базис індукції.

При n=1 нерівність вірна.

.

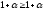2) Зробимо індуктивне припущення. Припустимо, що нерівність вірна і при n=k, тобто має місце нерівність (*)

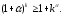Виконаємо індуктивний перехід. Доведемо, враховуючи припущення, що нерівність вірна і при n=k+1, тобто, що .

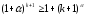Помножимо обидві частини нерівності (*) на вираз 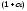. Це можна зробити, тому що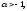тоді.

Маємо

,

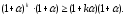
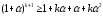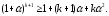
Враховуючи, що 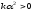, приходимо до нерівності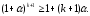Отже, нерівність вірна і приn=k+1. За принципом математичної індукції вона вірна для всіх .

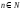7. Задачі на подільність чисел і метод математичної індукції Приклад №1

Довести методом математичної індукції, що для n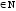(4ⁿ+15n-1)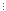9.

Доведення.

1)Базис індукції:

Переконаємося що дане твердження має місце при n=1.

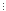4¹+151-1=18; 189

2)Індуктивний перехід:

Припустимо, що твердження має місце при n=k, тобто (4^k+15k-1)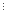9.

Виходячи з даного припущення доведемо, що дане твердження має місце і при

n=k+1, тобто (4^k+1+15(k+1)-1)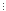9.

Очевидно, що:

4^k+1+15(k+1)-1=44^k+15k+15-1= P.S. 44^k=4^k+34k

=(4^k+15-1)+34^k+45k-45k+3-3+15=

=(4^k+15k-1)+3(4^k+15k-1)-9(5k+2)=4(4^k+15k-1)-9(5k+2).

В одержаному виразі зменшуване 4(4^k+15k-1) кратне 9, оскільки (4^k+15k-1)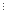9 за припущенням.

Від’ємник 9(5k+2) також ділиться на 9, бо один з його множників є число 9.

Отже, вся різниця ділиться на 9.

А це означає, що (4ⁿ+15n-1)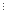9 при довільному натуральному числі n за принципом математичної індукції.

Приклад №2

Довести методом математичної індукції, що для n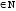(9ⁿ-8n-1)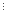16.

Доведення.

1)Базис індукції:

Переконаємося, що дане твердження має місце при n=1.

9¹-81-1=0; число 0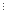16.

2)Індуктивний перехід:

Припустимо, що твердження має місце при n=k, тобто (9^k-8k-1)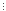16.

Виходячи з даного припущення, доведемо, що дане твердження має місце і при n=k+1,тобто (9^k+1-8(k+1)-1)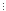16.

Очевидно, що

9^k+1-8(k+1)-1=99^k-8k-8-8=9^k-8k-1+89k-64k+64k-8=(9^k-8k-1)+8(9^k-8k-1)+64k.

(9^k-8k-1) 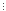16 за припущенням математичної індукції, 64k=164k , отже ,

64k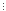16, (9^k-8k-1)+8(9^k-8k-1)+64k . Ця вся сума кратна 16, того що кожен доданок ділиться на 16.

Висновок: при довільному натуральному числі n (9ⁿ-8n-1)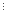16.

Приклад №3

Довести методом математичної індукції, що (6²ⁿ-1)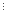35 для n.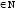

Доведення.

1)Базис індукції:

Переконаємося, що дане твердження має місце при n=1. (6²-1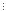)=3535

2)Індуктивний перехід:

Припустимо, що твердження має місце при n=k, тобто (6^2k-1)35.

Виходячи з даного припущення, доведемо, що дане твердження має місце і при

n=k+1,тобто (6^2(k+1)-1)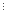35.

6^2(k+1)-1=6^2k+2-1=6^2k36-1=(35+1)6^2k-1=356^2k +(6^2k-1)

(6^2k-1) 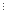35 за припущенням математичної індукції,

(356^2k) 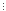35, тому що один з множників цього виразу ділиться на 35.

Отже, сума 356^2k +(6^2k-1)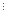35,nоді за припущенням математичної індукції (6²ⁿ-1)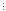35 при будь-якому натуральному n.n(6^2k-1)35.