для первого курса / для первого курса / Ответы по вышке / Ответы по вышке / Ряды / 08. Степенные ряды. Теорема Абеля

Степенные ряды. Теорема Абеля.
Одним из частных случаев функциональных рядов является степенные
0 –	0 + 1( − 0) + 2( − 0)			2	+ + ( − 0)					+	(1)
ряды, обобщенный степенной ряд в окрестности точки х=х0
x	заданная точка.
ai i=0,n коэффициенты, некие постоянные числа.								(2)
Сформулируем 0 + 1( ) + 2( )		2	+ + ( )				+
Если x0=0, то степенной ряд простой
	теорему Абеля			для простого				степенного ряда: если

степенной ряд (2) сходится при х=х0, то он абсолютно сходится при всех значениях IxI<Ix0I; если ряд расходится в точке х=х0, то IxI>Ix0I расходится.

Из полученной области сходимости можно заключить, что существует некоторое число R= Ix0I, которое называется радиусом сходимости, для которого справедливы сходимость при IxI < R и расходится при IxI > R.

В результате теоремы мы можем иметь 4 области сходимости для исследуемого ряда.

(-R;R); [-R;R); (-R;R]; [-R;R].

Так как поведение ряда в граничных точках исследуется дополнительно. Если R=0, то считается что ряд расходится повсюду кроме точки х=0. Если

R=∞, то сходится на всей числовой оси. Вычисляются R по формуле Даламбера

и Каши.
По Даламберу.	→∞
По Каши.
	= lim +1
	→=		1		на сходимость прежде всего
При исследовании	степенного ряда
	= lim | |

определяется R сходимостью, затем строиться область сходимости согласно теореме Абеля.

Для определения поведения ряда в граничных точках, мы значения х подставляем в заданный ряд и получаем числовой ряд, который исследуется как числовые ряды. Если ряд сходится, то данная точка входит в область

сходимости, если ряд расходится то не входит.

Рассмотрим пример простого степенного ряда:

−1

+

2

+

3

2

+ +

−1 +

=

Пример:

∞

2 10

2 10

10

=1 10

Мы имеем

=

1

10 −1

простой степенной ряд, где

1

+1 = ( + 1) 10

= lim

( + 1) 10

= 10

= lim

+1

10

−1

→∞

→∞

= 10; 10 +

102

+

103

2 + +

10

1

+

1

+ +

1

+ )

−1 + = 10(1 +

Изучим поведения ряда в граничных точках интервала сходимости.

расходится.

2 10

2 10

10

2

3

В скобках получили

обычный гармонический

ряд и

мы знаем что он

102

103

+ + (−1)

10

= −10; −10 +

2 10

−

2 102

10 −1

+

= 10(−1 +

1

−

1

+ + (−1)

1

+ )

В скобках мы

2

3

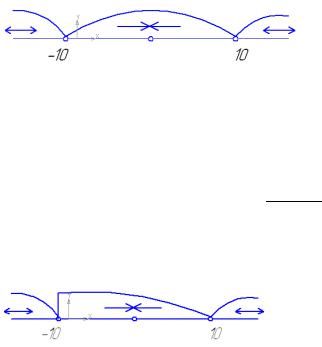
x [-10;10)

ряд сходится.

имеем ряд Лейбница который является сходящимся условно.

0

1

0

2

− 0)

Обобщим

теорему

Абеля

на

0

2

+ + ( − 0)

+ (1)

будет

(*)

обобщенный степенной ряд.

имеет0 + 1 + 2

2

+ +

+ ( )

Если x-x =X, то мы получим ряд:

Если ряд

радиус сходимости R, то согласно теореме Абеля,

ряд

| | < сходится

|x −x0 | <

| |

> расходится

0

→ |x − x

0

| <

0

<

+ ( )

Неравенство

(**)

→ −

<

|x − x0

| >

следующим

образом:

симметрия

области

понимается

сходимости перемещается в точку х0.

Если ряд сходимости = 0 , то ряд сходится в единственной точке Х=0. Если радиус сходимости = бесконечности, то ряд сходится во всех точках.

Следовательно, сходимость обобщенного степенного ряда определяется также, как и для простого степенного рядя. Для определения радиуса сходимости используются формулы Даламбера и Каши. Сходимость определяется относительно точки х0.

Поскольку степенной ряд – частный случай функционального ряда, то вопросы сходимости рядов аналогичны.

Справедлива теорема:

Степенной ряд, сходящийся равномерно на любом отрезке, принадлежащем интервалу сходимости, является равномерно-сходящимся.

Справедливы аналогичные свойства:

-Сумма степенного ряда является непрерывной в интервале сходимости.

-Внутри интервала степенные ряды можно по членно интегрировать и дифференцировать сколько угодно раз.