Вероятность попадания в заданный промежуток в случае нормального распределения.

Подставляя плотность нормального распределения в формулу:

Р(α < X < β) = f (х) d х,

Получим: Р(α < X < β) = φ () – φ ()

Здесь символ φ обозначает функцию: φ (Z) = l^{-t2/2 dx},

Называемую ФУНКЦИЕЙ ЛАПЛАСА. Ее значения находятся с помощью таблиц, которые имеются в учебниках теории вероятностей и в математических справочниках.

Если значения аргумента отрицательны, то для вычисления φ используются свойство ее нечетности.

Пример на применение формулы см. в разделе «Образец решения контрольной работы», задача 5.26.

Образец решения контрольной работы.

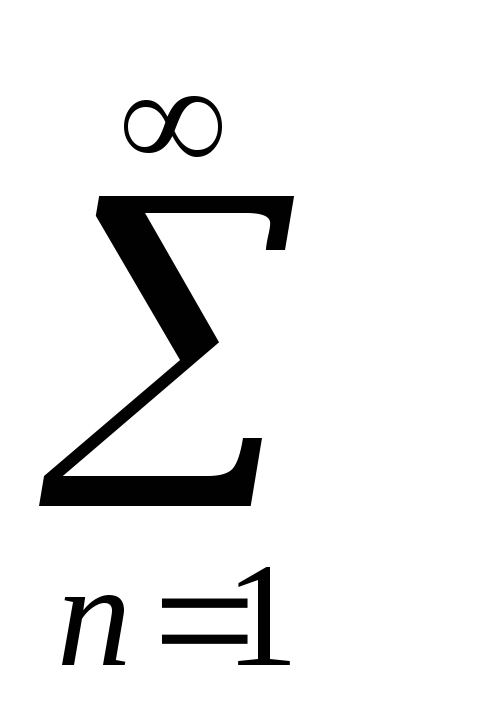
26. найти область сходимости степенного ряда: 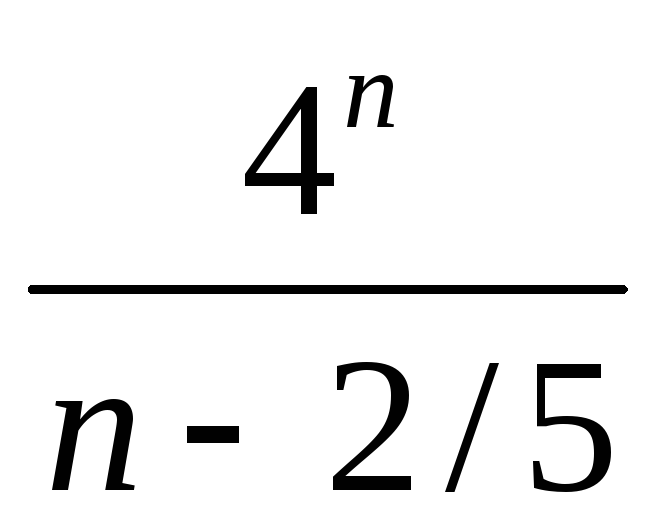х^п

Решение. R = = = = =

Интервал схождения есть - ¼ < x < 1/4 .

Проведем исследование на концах интервала сходимости. Подставим в ряд х = ¼. Получится числовой знакоположительный ряд . Сравним его с гармоническим рядом , который расходится

(р = 1): > данный ряд также расходится х = ¼ не входит в область сходимости.

Подставим х=-1/4. Получится знакочередующий ряд . Применим признак Лейбница:

Величина 1/(п – 2/5) убывает с ростом п и = 0 ряд сходится х = -1/4 входит в область сходимости.

Итак, область сходимости есть -1/4 ≤ x < ¼.

26. С точностью до 0,001 вычислить интеграл dх, разложив подинтегральную функцию в ряд Маклорена.

Решение.

= (1 + Z)^1/2 =

обозначим Z = , применим биноминальный ряд при m = ½.

= 1 + Z + Z² + Z³ + ...... = 1 + (1/2) Z – (1/8) Z²

+ (1/16) Z³ - ... = 1 + (1/2) (х²/3) - (1/2) (х²/3)² + (1/16) (х²/3)³ - ...= 1 + (1/6)х² – (1/72)х⁴ + (1/432)х⁶ - ......

Это равенство справедливо при -1 < Z < 1 или при -1 < х²/3 < 1, т. е. при х²/3 < 1, или х² < 3, или - < х < . Промежуток интегрирования 0 ≤ х ≤ 1 находится внутри этого интервала. Поэтому ряд можно подставить в интеграл вместо подинтегральной функции.

dх, = ( 1 + х² - х⁴+ х⁶ - ......)d х = d х + х² d х - х⁴ d х + х⁶ d х - ...... = х + + + - ..... = 1 + 1/18 – 1/360 + 1/3024 -.... ≈ 1 + 0,05556 – 0,00278 + 0,00033 - .... ≈ 1 + 0,05556 – 0,00278 ≈ 1,053.

Мы отбросили члена начиная с четвертого, допустив погрешность, меньшую его абсолютной величины 0,00033, тем более меньшую, чем 0,001.

Итак, dх ≈ 1,053.

26. Два стрелка делают залп по цели. Первый попадает с вероятностью 0,9; второй – 0,8. Найти вероятность того что попадут а) оба; б) только один; в) хотя бы один.

Решение.

Обозначим события: А – первый попадет, В – второй попадет.

Тогда:

а) АВ – оба попадут. По теореме умножения вероятностей имеет: Р(АВ) = Р (А) * Р(В) = 0,9 * 0,8 = 0,72;

б) А + В – попадет только один ( либо первый попадет, второй нет; либо первый промахнется, второй попадет). По теореме сложения вероятностей получаем:

Р (А + В) = Р (А) + Р (В) = Р(А) Р() + Р() Р() = 0,9 (1 – 0,8) + (1 – 0,9) * 0,8 = 0,26;

В) обозначим как С событие, состоящее в ходя бы = ,

Р(С) = 1 – Р() = 1 – Р( ) = 1 - Р() * Р() = 1 – (1 – 0,9) (1 – 0,8) = 0,98.

26. Дан закон распределения дискретной случайной величины Х:

Х	1 2 5
Р	0,5 0,3 0,2

Найти матожидание, дисперсию и среднеквадратическое отклонение Х.

Решение.

М [Х] = х₁ р₁ + х₂ р₂ + х₃ р₃ = 1 * 0,5 + 2 * 0,3 + 5 * 0,2 = 2,1

Д [Х] = (х₁ - М [Х] )² р_{1 +} (х₂ - М [Х] )² р₂ + (х₃ - М [Х] )² р₃ = (1 – 2,1)² * 0,5 + (2 – 2,1)² * 0,3 + (5 – 2,1)² *0,2 = 2,29.

Σ [Х] = = ≈ 1,513.

26. Известны матожидания α = 2 и среднеквадратическое отклонение σ = 4 нормально распределенной случайной величины Х. Найти вероятность того, что Х примет какое –нибудь значение в промежутке (1.10).

Решение.

Применим формулу : Р(α < X < β) = Ф () – Ф ()

Р(1 < X < 10) = Ф () – Ф() = Ф (2) – Ф (-0,25) = Ф (2) + φ (0,25)

≈ 0,4772 + 0,0987 = 0,5759.