ТВиМС.Малярец.Егоршин 22.12.12

Показательный закон зависит от одного параметра				, характеристики рас-
пределения выражаются через этот параметр:	M x				1	. Если из теорети-
		x
ческих соображений ожидается показательное распределение и x							ˆ x , то пара-
метр определяется из одного уравнения M x		1					1	.
	x			x
							x

Метод максимального правдоподобия – считается наиболее обоснован-

ным и пропагандируется как самый модный в настоящее время способ определения параметров. Заключается он в следующем: для всей системы наблюдений {xi} составляется функция правдоподобия – вероятность или плотность вероятности совместного появления такой системы данных. Функция правдоподобия зависит от параметров предполагаемого закона распределения. Эти параметры следует определять из условий максимума функции правдоподобия.

Например, предполагая показательное распределение, найдем наиболее правдоподобную оценку параметра . Функция плотности вероятности этого распределения для наблюдения xi имеет вид:

f(xi) = exp{– xi}.

Для независимых наблюдений дифференциальная функция их совместного распределения получается как произведение:

f(x1, x2, … , xn} = П(

exp{– xi}) = n exp{– xi}.

Обычно функцию правдоподобия принимают равной логарифму нату-

ральному от этого выражения:

Ф( ) = n ln( ) –

xi .

Приравниваем к нулю первую производную от функции правдоподобия

n

x 0, откуда получаем

n

1

. Именно такую оценку па-

i

xi

x

раметра получили ранее методом моментов.

1

x

a 2

Для нормального закона f xi

exp

i

, тогда функция

2

2

2

правдоподобия (логарифм от произведения функций f(xi)) будет равна:

a,	n ln		1				x a 2	,
			2		2		i
где постоянное слагаемое			отброшено.
	n ln 2
			101

2 оказалась равна обычной (смещен-

Приравниваем к нулю частную производную функции правдоподобия по параметру а:

		2		xi	a 0 , откуда a	1	xi	x .
	a	2 2				n

Правдоподобная оценка параметра а совпала с оценкой по методу моментов.

Приравниваем к нулю частную производную функции правдоподобия по параметру :

n			2		x a 2	0 , откуда	2	1	x a 2	s2 .
2				3	i			n	i	x

Правдоподобная оценка параметра ной) оценке дисперсии.

Метод наименьших квадратов применяется, в основном, в тех случаях, когда модель зависит от параметров линейно. Будем использовать этот метод для определения параметров регрессионных моделей. Он будет подробно описан в разделе «Регрессионный анализ».

Статистические критерии

Наряду с оценками характеристик и параметров вводят еще некоторые числовые комплексы K, составленные из данных наблюдений. Эти комплексы зависят от состава случайной выборки и поэтому также являются случайными величинами. Если известен (изучен) закон распределения K, то такие комплексы называются статистиками, или критериями. Известны статистики Пирсона, Стьюдента, Фишера (по именам ученых, установивших закон распределения того или иного комплекса). Многие оценки можно называть статистиками, показывая этим, что нам известны законы распределения таких оценок при изменении состава выборки.

Определим зону чисто случайного изменения критерия K, используя практический принцип невозможности редких событий. Выбираем уровень значимости , малый настолько, что сомневаемся в случайной природе появления события с такой малой вероятностью; мы более склонны считать, что наблюдаемое редкое событие вызвано какими-то внешними воздействиями, это «что-то означает» (вот откуда терминология «уровень значимости»). Обычно принимается уровень значимости 0,1, 0,05 или 0,01. Вероятность противоположного события P = 1 – называется уровнем доверия. Обычно принимают уровень доверия 0,9, 0,95 или 0,99. Зону чисто случайного изменения критерия

102

составляют все его значения, которые появляются с вероятностью, большей уровня значимости.

Далее все зависит от особенностей проблемы, для которой составлен тот или иной критерий. Существуют односторонние критерии, когда мы сомневаемся в случайном появлении слишком больших (или наоборот слишком малых) значений K.

Для правостороннего критерия (рис. 10.3а), зная распределение статистики К, находим квантиль К из условия Р(K > К ) = , или F(К ) = Р(K К ) = 1 – . Площадь под дифференциальной кривой fK справа от К равна .

а) б)

Рис. 10.3. Критическая зона для одностороннего (а) и двустороннего (б)

критериев

Если для наших данных окажется, что вычисленное значение K больше критического К , нуль-гипотеза о случайности изменения K отвергается и принимается противоположная (альтернативная) гипотеза о неслучайном появлении столь большого К.

Если для наших данных окажется, что вычисленное значение K меньше критического К, «нуль-гипотеза» о случайности изменения K не может быть

отвергнута.
Для двустороннего критерия (когда сомнительны большие случайные от-
клонения К и вправо и влево) вычисляются квантили K1		и K	. Площади
		2	2
под дифференциальной кривой fK слева от K1	и справа от K		одинаковы и
	2	2
равны /2 (рис. 10.3б). Нуль-гипотеза о случайности изменения K не может

быть отвергнута, если вычисленное значение критерия попадает в интервал

K1 2 K K 2 .

103

Так должно быть и для симметричных распределений статистики К, но в этом случае приняты не совсем правильные обозначения. Критическое значение К теперь определяется из условия Р(|K | > К ) = .

Заметим, что при этих обозначениях площадь под дифференциальной кривой fK справа от Кравна /2 (рис. 10.4). Это не совсем правильно, но общепринято.

Границы между областью принятия и областью отбрасывания нульгипотезы несколько размыты (рис. 10.5). Любой статистический критерий имеет некоторую область неопределенности, поэтому рекомендуется использовать сразу два уровня значимости (один для принятия, другой для отбрасывания нуль-гипотезы).

Рис. 10.4. Случай симметричного

распределения статистики К

Рис. 10.5. Два уровня значимости

(для принятия и отбрасывания нуль-гипотезы)

Уверены, что события с вероятностью 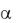0,01 случайно не происходят, поэтому принимаем такой уровень значимости для отбрасывания нульгипотезы. В то же время вероятность > 0,05 уже не может считаться малой, поэтому этот уровень значимости используется для принятия нуль-гипотезы.

Нас могут интересовать самые различные вещи, например, есть ли существенные различия между урожайностью разных сортов пшеницы, между эффективностью различных лекарственных препаратов, однотипной продукцией различных предприятий; нас может интересовать, есть ли значимое воздействие некоторых наших мероприятий на повышение качества и количества производимого продукта, нас крайне интересует надежность и безопасность, здоровье и сохранение среды обитания. Чтобы получить внятные ответы на

104

наши вопросы, формулируется соответствующая нуль-гипотеза, которая скептически утверждает, что никакого систематического воздействия нет, вся изменчивость определяется чисто случайными флуктуациями, нет никакого значимого различия между сравниваемыми сортами, продукцией разных предприятий, наши лекарства и наши мероприятия не приносят никакого эффекта.

Мы должны оценить вероятность появления наших данных при справедливости нуль-гипотезы и, если эта вероятность не окажется достаточно малой, вынуждены будем сделать огорчительное заключение: «Нуль-гипотеза не может быть отвергнута»; данных мало, чтобы надежно заявить противоположное; такие эффекты могут появляться чисто случайно.

Мы вовсе не утверждаем, что лекарства действительно неэффективны, что сравниваемая продукция действительно эквивалентна и т. п., мы расписываемся в собственной беспомощности – по имеющимся данным ничего определенного сказать нельзя.

Но если вероятность появления данных при справедливости нульгипотезы окажется меньше определенного уровня, то нуль-гипотеза отвергается и принимается противоположное утверждение, которое называется альтернативной гипотезой.

При правильно поставленных вопросах альтернативная гипотеза может утверждать, что между подсовокупностями имеются значимые различия (в любую сторону), либо более определенно утверждать, что альтернативное значение параметра больше (или наоборот меньше) того, которое свойственно при нуль-гипотезе.

Все истины, установленные экспериментально, получены в опытах, где нуль-гипотеза была отвергнута (найдены контрпримеры). Тонкий знаток и ценитель природы, писатель М. Пришвин заметил: «Да» природы условное и еле слышимое. «Нет» природы ясное и категоричное».

Государственными стандартами установлено, какую вероятность можно и нужно считать малой. Это уровень значимости 0,01, который является вероятностью «ошибки 1-го рода» – вероятности ошибочно отвергнуть правильную нуль-гипотезу.

В то же время вероятность > 0,05 уже не может считаться малой, иначе мы допустим «ошибку 2-го рода» – ошибочно примем неверную альтернативную гипотезу (в юстиции также различают ошибки «наказать невиновного» и «упустить виновника»; в приемочном контроле различают «риск производителя», когда на основе недостаточного выборочного обследования бракуют всю

105

партию пригодной продукции, и «риск потребителя» – принимается партия некондиционной продукции).

Поэтому, если вероятность чисто случайного появления наших данных больше 5 % , делается стандартное заключение: нуль-гипотеза не может быть отвергнута (иногда говорят, нуль-гипотеза принимается); если вероятность оказалась меньше 1 % , то «нуль-гипотеза отвергается»; но если эта вероятность больше 1 % и меньше 5 % , делается более осторожное заключение: нуль-гипотеза принимается (или отвергается) при 5-процентном уровне значимости.

Наши заключения могут задевать чьи-то интересы, и в последнем спорном случае на нас могут оказывать определенное давление в пользу того или иного вывода; именно поэтому необходима оговорка о 5-процентном уровне значимости.

Вопросы для самопроверки

1.Что такое состоятельность оценок?

2.Что такое несмещенность оценок?

3.Что такое сумма квадратов (отклонений)?

4.Что такое число степеней свободы?

5.Приведите формулу для несмещенной оценки дисперсии.

6.Что такое эффективность оценок?

7.Как оцениваются параметры распределения? Какие для этого существуют методы?

8.Что такое статистики?

9.Как выбирается зона чисто случайного изменения статистики?

10.Как обозначаются критические значения статистик для несимметричных распределений?

11.Как обозначаются критические значения статистик для симметричных распределений?

12.Что такое зона неопределенности критерия?

106

11. Критерии согласия

Критерий согласия Пирсона

С помощью критериев согласия проверяют гипотезу о соответствии эмпирического распределения предполагаемому теоретическому закону, например, наиболее часто проверяют, можно ли считать наблюдаемое распределение нормальным.

Самый распространенный критерий согласия предложил К. Пирсон, который доказал, что если величины xi распределены по стандартному нормаль-

ному закону xi ~ N(0, 1) с характеристиками М(xi) = 0 и

(xi) = 1, то сумма их

n

квадратов

2

x2

имеет гамма-распределение с вполне определенными па-

i

i

1

1

1e

раметрами:

f

x

x 2

2 . Этот частный случай гамма-распределения

2

2

2

называется

распределением

Пирсона «Хи-квадрат». В

общем

виде

гамма-

x

1

распределение

f

x

e

x зависит от двух параметров (

и

). Ранее

1 !

(при изучении композиций случайных величин) мы уже встречались с одним

частным	случаем		гамма-распределения	–	распределением Эрланга
	x m 1
fm x		e x	с целочисленным параметром			= m. В распределении
	m 1 !
Пирсона оба параметра полуцелые: = 1 / 2 ,				=	/ 2 , где	= df – число степеней

свободы (ЧСС) системы случайных величин {xi} (для независимых величин

df = n, a для зависимых df = n – число связей). Факториал (

– 1)! для дробных

значений

в отечественной научной литературе обозначается как Г( ), где

t

1e

t dt

–

гамма-функция,

для

которой

выполняется соотношение

0

1

3

1

1 . Закон распределения

( +1) =

(

).

В

частности,

,

2

2

2

2

Пирсона однопараметрический (зависит только от параметра

= df). Типичный

график дифференциальной функции распределения показан на рис. 11.1, где K = 2 . Характеристики закона М( 2) = , D( 2) = 2 .

107

Для		каждого			значения		= df
составлены			таблицы			квантилей
2	2	,	2	2
0,99 ,	0,95		0,05 ,	0,01 . Зоной слу-
чайного изменения					2	является	ин-
тервал	2		2		2	(так называ-
	0,95				0,05
емый 90-процентный доверительный
интервал). При увеличении df рас-
пределение Пирсона приближается к
нормальному, поэтому таблицы кван-
тилей составлены только для df							30.	Рис. 11.1. Распределение Пирсона

Для проверки гипотезы о согласии эмпирического распределения предполагаемому теоретическому закону Пирсон составил статистику (критерий), которая обозначается 2 :

	k		m		~		2
2				j	m	j		,
					~
	j 1				m j

где mj – наблюдаемые частоты попадания случайной величины в интервалы

sj–1 < X	sj ;	~	– ожидаемые частоты по предполагаемому теоретическому за-
		m j

кону, в котором неизвестные параметры заменены на их эмпирические оценки. Структура статистики Пирсона – это сумма квадратов отклонений частот от их

~	(отклонения в одну-две едини-
ожидаемых значений с весами, обратными к m j
~	~
цы существенны для малых m j и не существенны для больших m j ).
Покажем, что при выполнении некоторых условий статистика Пирсона

распределена по закону 2 . Существует некоторая вероятность pj попадания наблюдений в интервал (sj–1 , sj ]. Количество таких наблюдений (частота mj)

распределено по закону Бернулли

с характеристиками M(mj) = npj и

D(mj) = npjqj = npj(1 – pj). При n

30, npj

5 распределение Бернулли уже мож-

но считать нормальным (распределением Лапласа) и тогда величина:

2

k

m

j

np

2

k m

j

np

2

j

j

j 1

np j q j

j 1np j 1 p j

будет распределена по закону

2 . Если интервалы (sj–1 , sj ] достаточно узкие,

настолько, чтобы можно было пренебречь малыми вероятностями pj < 0,1 по сравнению с единицей, то получаем комплекс:

108

2	k		m	j	np	j	2	,
j	1			np j
который распределен по закону 2	при mj				5, но при mj < 0,1 n (в каждый ин-

тервал должно попасть не менее 5-ти наблюдений, но меньше 10 % от объема выборки). Эти два несколько противоречивых требования могут быть выполне-

ны одновременно только для выборок большого объема n > 200.

Теоретические вероятности попадания наблюдений в заданные интервалы

вычисляются с

помощью

интегральной

функции

предполагаемого

закона

~

~

s j

~

s j

1 , а ожидаемые частоты – по формуле

~

pi

F

F

mj

np j .

Отсюда

получаем

статистику

Пирсона

в

стандартном

виде

k

m

~

2

2

j

m

j

. Если снять обременительное требование mj < 0,1 n,

то ста-

~

j

1

m j

k

~

2

2

m j

m j

тистика слегка усложняется

, но теперь ее можно применять

~

j 1 ~

m j

m j 1

n

для выборок умеренного объема 30

n < 200.

Замена pj

~

~

боль-

на p j приводит к тому, что отклонения частот

m j m j

ше не будут независимыми, на них будут наложены две или три связи. Дей-

ствительно, поскольку	~	1 (если это не так, следует расширить крайние
	p j

интервалы – еще одно условие правильного применения критерия Пирсона), то

получается, что	~	n n 0 – сумма всех отклонений равна нулю.
	m j m j

При оценке параметров предполагаемого закона методом моментов приравниваем теоретические характеристики к их выборочным оценкам. Если закон однопараметрический (Пуассона или показательный), один параметр закона оце-

нивается	из	равенства	M x x , откуда получаем еще одну связь
~	X j	n x M x	0 , где Xj – центры интервалов. При проверке со-
mj mj

гласия распределения с однопараметрическим законом число степеней свободы равно df = k – 2. Большинство теоретических законов распределения двухпараметрические (Бернулли, нормальный, логнормальный, равномерный, гамма),

для них оценку второго параметра получаем, приравнивая дисперсии				2	2	,
				x	sx
что приводит еще к одной связи	~	2	0 , откуда для двухпарамет-
	m j m j	X j

рических законов df = k – 3.

109

Для данного числа степеней свободы по таблицам Пирсона находят кван-

тили	2	,	2	,	2	,	2	. Если окажется,		что вычисленное значение стати-
	0,99		0,95		0,05		0,01
стики Хи-квадрат находится в пределах									2	2	2	, нуль-гипотеза о слу-
									0,95		0,05

чайности расхождений между наблюдаемыми и ожидаемыми частотами не может быть отвергнута; предполагаемый теоретический закон не противоречит данным; можно считать, что он именно такой и можно использовать его для дальнейших вычислений. Уровень доверия нашего заключения Р = 0,9 (90 %). Если окажется, что вычисленное значение статистики Хи-квадрат больше

большей границы	2	2	, нуль-гипотеза отвергается; предполагаемый тео-
		0,01

ретический закон не согласуется с данными, расхождения между наблюдаемыми и ожидаемыми частотами слишком велики, распределение неудовлетворительно описывается этим законом. Однако нуль-гипотеза отвергается также при слишком хорошем соответствии, когда вычисленное значение статистики Хи-

квадрат оказывается меньше меньшей границы	2	2	; в этом случае со-
		0,99

мневаемся в достоверности данных, по всей видимости здесь имеется какая-то фальсификация; вероятность такого полного соответствия при справедливости нуль-гипотезы меньше 1 % , а такое событие является практически невероятным (невозможным).

Рассмотрим пример применения критерия согласия Пирсона. На рис. 11.2 изобра-

	жены гистограмма, поли-
	гон (графически сглажен-
	ная гистограмма) и кривая
	нормального	распределе-
	ния, параметры		которой
	оценены методом		момен-
	тов. Можно ли считать, что
	эмпирическое	распределе-
	ние нормальное?
	На рис. 11.3 приведен
	интервальный	вариацион-
				Рис. 11.2. Дифференциальные функции
	ный ряд с шагом		группи-	распределения

ровки h = 0,2. Сумма наблю-

даемых частот равна n = mj = 75, оценки характеристик: x 1,297 , sx = 0,433.

110