ТВиМС.Малярец.Егоршин 22.12.12

		m			Cnm					pm				qn–m			Pn(m)			F(m)
	0			1						1			0,133484			0,133484			0,133484
	1			7						0,25			0,177979			0,311462			0,444946
	2			21						0,0625			0,237305			0,311462			0,756409
	3			35			0,015625						0,316406			0,173035			0,929443
	4			35			0,003906						0,421875			0,057678			0,987122
	5			21			0,000977						0,5625			0,011536			0,998657
	6			7			0,000244						0,75			0,001282			0,999939
	7			1			0,000061						1			0,000061			1,000000
					Рис. 4.6. Расчеты по формуле Бернулли
		Вычисляем:
		P(m 4) = F(4) = 0,987;
		P(m			2) = P(2		m 7) = F(7) – F(1)= 1 – 0,4450 = 0,555;
		P(2<m<6) = P(3					m 5) = F(5) – F(2) = 0,999 – 0,756 = 0,242.
		Заметим, что во многих учебниках функция F(x) определена немного по-
другому:				F(x) = P(X < x).						Тогда для нашего примера надо было бы принять
F(0) = 0 и изменить формулу расчета вероятности попадания случайной вели-
чины в интервал, полуоткрытый сверху: P(m1															m < m2) = F(m2) – F(m1) или же
P(m1 m					m2) = F(m2+1) – F(m1). Оба определения функции F(x) эквивалентны,
но следует придерживаться одного стандарта.
		Вычисляем характеристики распределения Бернулли:
				M(m) = np = 7 0,25 = 1,75; D(m) = npq = 7 0,25 0,75 = 1,3125;
					m			D( m ) 1,1456 ; M(m) – q							Mo M(m) + p;
				1,75 – 0,75				Mo		1,75 + 0,25; 1 Mo					2; P(1) = P(2) = Pmax .
		Согласно правилу «3-х сигм», вероятные значения m не превышают:
									M(m) + 3			m = 1,75 + 3 1,146 = 5,19 5.

На рис. 4.7 приведен полигон распределения Бернулли для данного примера.

Рис. 4.7. Полигон распределения Бернулли

41

Распределение Пуассона

Для n > 30 производить расчеты по формуле Бернулли становится затруднительным из-за слишком больших величин факториалов, поэтому используют асимптотические формулы Пуассона и Лапласа, которые становятся все более и более точными с увеличением n (именно в тех случаях, когда расчеты по исходной формуле Бернулли практически невозможны). Формула Пуассона применяется для больших n > 30 и малых р < 0,05, таких, что nр < 5 (поэтому распределение Пуассона применяется для изучения распределения числа редких событий). Во всех остальных случаях (n > 30, nр 5, nq 5) применяется асимптотическая формула Лапласа. Используем для примера партию электролампочек, из которых 2 % выходит из строя при перевозке. Какова вероятность того, что число испорченных лампочек будет не больше 5? Если перевозится n = 10 лампочек, то расчеты вероятностей надо производить по формуле Бернулли; если в партии n = 100 лампочек – по формуле Пуассона (n = 100 > 30; р = 0,02 < 0,05; nр = 2 < 5); если же в партии n = 1000 лампочек – по формуле Лапласа (n = 1000 > 30; nр = 20 > 5; nq = 980 > 5).

Закон распределения редких событий Пуассона

P m e a am m!

имеет самостоятельное значение и свою область применения – теорию массового обслуживания.

Получим вышеприведенное выражение как предельную формулу для распределения Бернулли при n 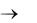, р 0, q 1, но при этом nр = а = Const.

Преобразуем формулу Бернулли:

n!

pmqn m

n n

1 n

2 ... n

m 1

a

m

a

n m

P m

1

n

m! n m !

1 2 3 m

n

n

am n n

1 n

2

n m

1

1

a

m 1

a n

am

lim 1

a

n

am

e a .

m! n n

n

n

n

n

m!

n

m!

n

Поскольку формулу Пуассона можно рассматривать как предельный случай формулы Бернулли, то для нее сохранились все характеристики распределения Бернулли с заменой р 0, q 1, np = a:

(a – 1) Mo a; M(m) = a; D(m) = a; A	1			.
		a

42

Распределение Пуассона зависит от одного параметра а. Типичный вид полигонов распределения Пуассона для разных значений параметра a показан на рис. 4.8, из которого видно, что с увеличением a вид распределения приближается к стандартной симметричной форме (распределению Лапласа).

Рис. 4.8. Вид распределения Пуассона

в зависимости от параметра а

Вычисления вероятностей P(m) распределения Пуассона удобно произво-

	дить по рекуррентной формуле: P m						P m 1	a	, где Р(0) = е-а.
								m
	Например, для а = 2:
	Р(0)	= е–2 = 0,135;			Р(1)	= Р(0)	2/1 = 0,270; Р(2) = Р(1) 2/2 = 0,270;
	Р(3)	= Р(2)	2/3	= 0,180; Р(4)		= Р(3)	2/4 = 0,090; Р(5) = Р(4) 2/5 = 0,036;
	Р(6)	= Р(5)	2/6	= 0,012;	Р(7) = Р(6) 2/7 = 0,003				и т. д.

Обычно в задачах на распределение Пуассона задается среднее число	по-
явления некоторого события за определенный период времени: a = t, где	–

интенсивность появления события – среднее число событий в единицу времени. Для примера рассмотрим следующую задачу.

В одном кубическом метре воздуха в среднем находится 1000 болезнетворных микробов. Для анализа взяли 2 литра (дм3) воздуха. Найти вероятность того, что в пробе будет выявлено m = 0, 1, 2, ... болезнетворных микробов, не больше трех микробов, от двух до пяти микробов, хотя бы один микроб.

Решение. Это типичная задача на распределение Пуассона, где задана ин-

тенсивность

= 1000

для

t = 1 м3.

Для t = 2 л = 0,002 м3

получаем

а = 1000 0,002 = 2 – это среднее количество микробов в 2-х литрах воздуха.

a

am

Вычисления вероятностей распределения Пуассона P( m )

e

про-

m!

изводим по рекуррентным формулам:

P( m )

P( m 1)

a

P( m 1)

2

;

P( 0 ) e-a

e-2 0,135335 .

m

m

Возможные значения m не ограничены сверху, однако, согласно правилу

«3-х сигм»,

достаточно

рассчитать

вероятности

P(m)

только для

43

					3 1,414 6,2 . Для m = 0, 1, 2, ..., 10 вычисления сведены в
m	a 3 a 2
таблицу на рис. 4.9, рядом с ней построен график полигона (рис. 4.10).
m		P(m)			F(m)
0		0,135335			0,135335
1		0,270671			0,406006
2		0,270671			0,676676
3		0,180447			0,857123
4		0,090224			0,947347
5		0,036089			0,983436
6		0,012030			0,995466
7		0,003437			0,998903
8		0,000859			0,999763
9		0,000191			0,999954
10		0,000038			0,999992

Рис. 4.9. Расчеты	Рис. 4.10. Полигон распределения Пуассона
по формуле Пуассона

С помощью функции F(m) находим:
P(m 3)	= F(3) = 0,857123;
P(2 m	5)	= F(5) – F(1) = 0,983436 – 0,406006 = 0,57743;
P(m 1)	= 1	– P(0) = = 1 – 0,135335 = 0,864665.
Определяем характеристики распределения Пуассона:
	M(m) = a = 2; D(m) = a = 2;		m D(m) 1,414 ;
	a – 1 Mo a; 1 Mo 2;		P(1) = P(2) = Pmax.

Здесь целочисленны оба края интервала длиной в единицу, поэтому самыми вероятными оказались сразу два соседних значения.

Вывод формулы для расчета вероятностей распределения Пуассона

Выше распределение Пуассона было получено как предельное из распределения Бернулли при определенных условиях: n , р 0, но при этом nр = а = Const. Здесь приведен вывод распределения Пуассона без ссылок на распределение Бернулли. Рассмотрим события, которые наступают в случайные моменты времени. Последовательность таких событий называется потоком событий. Примерами потоков событий служат: поступление вызовов на АТС, в пункт неотложной медицинской помощи, прибытие самолетов в аэропорт, последовательности отказов элементов и многое другое. Простейшим (пуассоновским) называют поток событий, который обладает свойствами

44

стационарности, отсутствия последействия и ординарности. Свойство стационарности характеризуется тем, что вероятность появления событий на любом промежутке времени зависит только от длительности t промежутка, но не от начала его отсчета. Свойство отсутствия последействия характеризуется тем, что вероятность появления событий на любом промежутке времени не зависит от того, появлялись или не появлялись события в моменты времени, предшествующие началу рассматриваемого промежутка. Свойство ординарности характеризуется тем, что за малый промежуток времени вероятность появления более одного события пренебрежимо мала по сравнению с вероятностью появления только одного события.

Обозначим через Pm(t) вероятность появления m событий за период времени t; тогда P0(t) означает вероятность того, что за этот период не произойдет ни одного события; 1 – P0(t) – произойдет хотя бы одно событие.

Далее обозначим	lim	1		P0	t	, тогда для малого интервала времени h
				t
	t 0

имеем 1 – P0(h) = h + o(h), где o(h) убывает быстрее, чем h.

Принимаем постулаты Пуассона: каково бы ни было число появления событий в период времени (0; t), условная вероятность того, что в течение последующего малого интервала времени (t; t + h) появится одно событие, равна h + o(h), а вероятность того, что появится более одного события, есть o(h). Из

этих условий выводятся дифференциальные уравнения для определения Pm(t). На протяжении объединенного интервала времени (0; t + h) m событий

(m 1) могут появиться 3-мя взаимоисключающими способами: 1) ни одного события за время (t; t + h) и m событий за время (0; t); 2) одно событие за время (t; t + h) и (m – 1) событий за время (0; t); 3) более одного события за время (t; t + h) и остальные события за время (0; t). Вероятность первой возможности равна произведению Pm(t) на вероятность того, что на интервале (t; t + h) не

произойдет ни одного события; эта последняя вероятность равна										1 – h – o(h).
Аналогично вторая возможность имеет вероятность Pm–1(t)									h + o(h), а вероят-
ность третьей возможности убывает быстрее, чем h. Отсюда для m										1 имеем:
		Pm(t + h) = Pm(t) (1 – h) + Pm–1(t) h + o(h);
				Pm t h Pm t	Pm t	Pm 1 t	o h		.
				h			h
Учтем, что lim	o h			0 , тогда после предельного перехода h					0 получим:
	h
h 0
				Pm t	Pm t	Pm 1 t .

45

Это рекуррентное соотношение позволяет записать дифференциальное уравнение для определения Pm(t), если уже известно выражение для Pm–1(t). Для начала найдем P0(t).

При m = 0 вторая и третья возможности не возникают, поэтому рекур-

рентное уравнение упрощается:
P0(t + h) = P0(t) (1 –						h) + o(h), откуда P0 t				P0 t .
С учетом естественного начального условия P0(0) = 1 из последнего диф-
ференциального уравнения получаем P0(t) = e– t.
При m = 1 имеем					P t		P t	e	t , откуда с учетом начального усло-
					1		1
вия P1(0) = 0 получаем P1(t) = (							t) e– t.
Действуя				таким		же	образом,		для	остальных m получаем
	t	t	m
Pm t e				. Это распределение Пуассона, для которого M(m) = t, сле-
		m!
довательно, параметр					есть интенсивность – среднее число появления событий
в единицу времени.

Вопросы для самопроверки

1.Сформулируйте задачу Бернулли, приведите ее другие названия.

2.Опишите особенности распределения Бернулли в зависимости от его параметров.

3.Приведите расчетные формулы для основных характеристик распределения Бернулли.

4.Укажите область применения асимптотических формул Пуассона и

Лапласа.

5.Приведите формулу Пуассона и укажите область применения этого распределения. Что такое рекуррентная формула?

6.Опишите особенности распределения Пуассона в зависимости от пара-

метра.

7.Приведите расчетные формулы для основных характеристик распределения Пуассона.

46

5. Распределение Лапласа

Для n > 30, nр

5, nq 5 распределение Бернулли практически точно ап-

проксимируется асимптотической формулой Лапласа:

1

m mp

2

tm

P m

e

2npq

,

n

2

npq

m

m a

1

t 2

e 2 .

где обозначено t

m

, a np,

m

npq ,

t

2

m

Эта аппроксимация называется локальной теоремой Лапласа.

На рис. 5.1 для сравнения приведены полигоны распределений Бернулли и Лапласа для р = 0,3; n = 10 и n = 20. Даже для таких небольших значений n соответствие очень хорошее (здесь np = 3 и np = 6).

Рис. 5.1. Сравнение распределений Бернулли и Лапласа

Функция (t) затабулирована и называется дифференциальной функцией Лапласа, или же функцией стандартизованного нормального распределения Гаусса. Дело в том, что (как выяснилось впоследствии) Лаплас открыл частный случай более общего закона природы, который Гаусс назвал «нормальным». Известно, что в русском языке слово «нормальный» имеет совершенно иной смысл, чем в немецком, но это новое понятие не противоречит сути, поскольку нормальное распределение действительно является неким стандартным устой-

47

функция Лапласа

чивым законом природы, к которому при определенных условиях приближаются многие другие законы распределений.

Функция (t) имеет некоторые особенности, которые учтены при составлении таблиц.

Во-первых, эта функция четная (график ее симметричен относительно оси ординат), поэтому таблицы составлены только для неотрицательных значений t; для отрицательных t использу-

ется соотношение четности

Рис. 5.2. Дифференциальная

(–t) = (t).

Во-вторых, функция (t)

неотрицательная и имеет горизонтальную асимптоту – ось абсцисс; иными словами, при увеличении t значения (t) приближаются к нулю, поэтому таблицы со-

ставлены только до значений t 5; так:	(3) = 0,00443;	(4) = 0,00013;
(5) = 0,00001; для больших значений аргумента (t)	0.
Максимальное значение функции достигается при t = 0 и равно		(0) = 0,3989.

Характерные особенности дифференциальной функции Лапласа изображены на рис. 5.2.

Интегральная теорема Лапласа

Для больших n вычисление вероятностей отдельных значений m лишено особого смысла, так как даже для самого вероятного значения – моды получа-

ется P Mo

0

0,4

~

1

– очень малое число при большом n.

npq

npq

n

В практических задачах для больших n требуется находить вероятности попадания случайной величины в некоторые интервалы P(m1 m m2), то есть вычислять вероятности не одного значения m, а вероятности всех целых значений m из интервала [m1 , m2]:

	m		im			1
P m m m		2 P m	2	t			.
1	2	n			m
	m	m1	t tm			m
			1

48

Рассмотрим приращение

tm

при увеличении m на единицу:

tm tm 1

tm

m 1

a m a

1

1

0 .

m

m

m

npq

i

m

1

i

m

im

2

Оказывается, P m1

m

m2

2

tm

2

t

t

t dt .

t tm

t tm

m

t

m

1

1

1

t

1

t

s 2

2 ds ,

Лаплас ввел функцию

t

s ds

e

которая сейчас назы-

2

0

0

вается интегральной функцией Лапласа.

Теперь вероятность попадания случайной величины m в интервал [m1 , m2]

im2

можно записать P m1 m m2

tm1

t dt	tm	2	tm	как разность значе-
			1

ний интегральной функции Лапласа на краях этого интервала. Это утверждение называется интегральной теоремой Лапласа.

Функция Ф(t) имеет некоторые особенности, которые учтены при составлении таблиц. Во-первых, эта функция нечетная (график ее центрально симметричен относительно начала ординат), поэтому таблицы составлены только для неотрицательных значений t; для отрицательных t используется соотноше-

ние нечетности Ф(–t) = –Ф(t).
Во-вторых, функция Ф(t) воз-
растающая и имеет			горизонтальные
асимптоты – Фmin = –0,5 и Фmax = 0,5;
иными словами, при увеличении t
значения Ф(t) приближаются к 0,5,
поэтому таблицы составлены только
до значений		t	5;	то	есть:
Ф(3) = 0,49865;			Ф(4) = 0,49997;
Ф(5) = 0,5000; для еще больших зна-
чений аргумента Ф(t) = 0,5. Значение
функции	при	t =	0	равно	нулю
Ф(0) = 0.	Характерные			особенности		Рис. 5.3. Интегральная функция
интегральной функции Лапласа изоб-						Лапласа
ражены на рис. 5.3.

49

Три основных формы интегральной теоремы Лапласа

Для лучшего усвоения материала введем условную классификацию утверждений интегральной теоремы Лапласа и перечислим задачи, которые решаются с помощью каждой из них.

1. В качестве первой формы теоремы примем общую формулу для вычисления вероятности попадания случайной величины в заданные интервалы:

P m1 m m2		tm	tm .
		2	1
2. Вторая форма предназначена для вычисления вероятности попадания
случайной	величины в		интервалы, симметричные относительно центра:
Р(|m – a|	t m) = 2Ф(t).

Действительно, для симметричных интервалов m2 = a + t m , m1 = a - t m ,

		a t	m	a	t ,	a t	m
tm						tm
	2
			m			1	m

a t . Вычисляем:

Р(|m – a| t m) = Р(m1 m m2) = Ф(t) – Ф(–t) = Ф(t) + Ф(t) = 2Ф(t).

В качестве примера применения выведенной формулы ответим на вопросы: «Какова вероятность того, что отклонения случайной величины m от центра

a = np не превысят m , 2	m , 3	m ?»
Используя таблицы интегральной функции Лапласа, получим:
Р(|m – a|		m) = 2Ф(1) = 2 0,3413 = 0,6826;
Р(|m - a|	2	m) = 2Ф(2) = 2 0,4772 = 0,9544;
Р(|m - a|	3	m) = 2Ф(3) = 2 0,4987 = 0,9974.

Только в 3-х случаях из 1000 возможны появления отклонений, превышающие три сигмы; с гарантией 95 % можно утверждать, что для распределения Лапласа (и нормального закона Гаусса) случайные отклонения не превысят две сигмы (это утверждение может быть ошибочным лишь в 5-ти случаях из

100).

3. Перепишем неравенство |m – a|

t

m в виде

m

np

t

npq и далее

(разделив обе части неравенства на n):

m

p

t

pq

.

n

n

Получаем следующее выражение, которое мы назовем «третьей формой

интегральной

теоремы

Лапласа»:

P

m

p

t

pq

2

t

или же

n

n

P

m

p

2

n

. В описании этой формулы два раза встречается

n

pq

50