ТВиМС.Малярец.Егоршин 22.12.12

На рис. 14.5 изображена функциональная (то есть наиболее тесная) квадратичная зависимость, которую ошибочно попытались аппроксимировать линейной моделью.

Ввиду симметрии расположения заданных точек наилучшая линейная модель получилась в виде y p y , для которой R2 = 0.

Рис. 14.5. Линейная аппроксима-

ция нелинейной зависимости

Однофакторная линейная зависимость

Для этого частного случая можно получить готовые формулы для МНКоценок параметров модели и коэффициента корреляции.

Систему нормальных уравнений для линейной модели y = b0 + b1 x + e

	y	b0	b1 x
			b x2
xy		b
		0	1

можно решить в общем виде и получить формулы для расчета коэффициента

регрессии b	sxy	и свободного члена b	y b x .
1	sx2	0	1

Из формулы для дисперсии остатка модели:

2

sxy

s2

y2

b y b yx

y2 y2 b yx y x s2

b s

xy

s2

e

0

1

1

y

1

y

sx

получаем коэффициент детерминации в виде:

	2		se2		s xy	2
R		1				.
			s 2		s x s y
			y

Извлекаем корень квадратный из коэффициента детерминации и получаем коэффициент парной корреляции (Пирсона):

r	sxy	.
xy	sx sy

Таким образом, коэффициент множественной корреляции R для случая однофакторной линейной зависимости совпадает (по модулю) с коэффициентом парной корреляции R = | rxy |. В общем же случае он совпадает с коэффициентом парной корреляции между расчетными и наблюдаемыми значениями

R ryy p .

151

Коэффициент парной корреляции rxy и его квадрат (коэффициент детерминации R2) оценивает тесноту линейной связи. Если rxy = 0, линейной связи нет; при rxy = 1 имеем точную линейную зависимость.

На рис. 14.6 изображены возможные ситуации при разных значениях rxy .

Рис. 14.6. Различные случаи тесноты связи

С использованием коэффициента парной корреляции ранее найденные формулы можно записать несколько в иной форме:

b	r		sy	;
1		xy	sx
s2	s2	1	r2 .
e	y			xy

Уравнение регрессии удобно записать в стандартизованных переменных:

y y	r	x x	.
sy	xy	sx

Если изменить направление причинно-следственных связей, то получим очень похожее уравнение сопряженной регрессии:

x x	r	y y	.
sx	xy	sy

152

Если же оба показателя (x и y) являются следствиями одной и той же общей причины, то наилучшим описанием связи будет диагональная регрессия (Фриша):

y y		x x	,
s y		sx

где знак соответствует знаку ковариации sxy или знаку коэффициента корреляции rxy .

Нелинейные двухпараметрические модели

Как уже было сказано выше, для успешного применения МНК желательно, чтобы форма связи была линейной относительно параметров модели. Для двухпараметрических зависимостей, которые линейно зависят от параметров или могут быть приведенными к такой форме функциональными преобразованиями, существует графический способ проверки их пригодности для описания данных (иными словами, существует графический способ проверки адекватности модели).

Пусть Y = F(x, y) и X = Ф(x, y) – такие функциональные преобразования, после которых форма связи формально приводится к линейному виду:

Y = a + bX.

Чаще всего используется или логарифмирование, или переход к обратным величинам. На рис. 14.7 приведены справочные сведения о нелинейных двухпараметрических зависимостях, которые могут быть сведены к линейным указанными функциональными преобразованиями.

Для наглядности на рис. 14.7 в клетках таблицы приведены эскизы графиков типовых зависимостей в исходных координатах (х, у).

Графиком линейной зависимости является прямая, а прямую человек уверенно выделяет среди множества других кривых. Отсюда следует такое правило: если в преобразованных координатах (X, Y) эмпирические точки не группируются вокруг какой-либо прямой, принятая форма связи не является адекватной.

С использованием современной вычислительной техники любые графики легко строятся и преобразуются, поэтому описанный способ идентификации формы связи является достаточно эффективным.

153

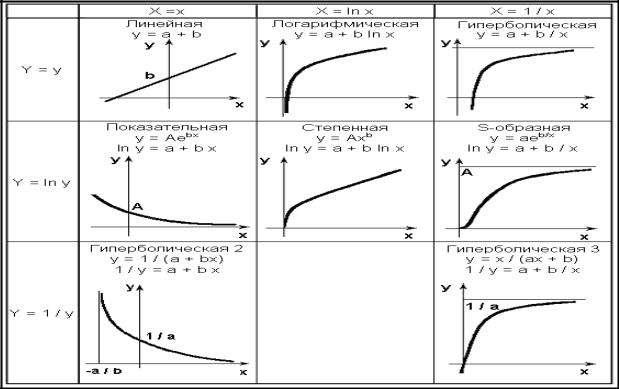
Рис. 14.7. Двухпараметрические зависимости Y = a + bX

Ни одна из двухпараметрических зависимостей, приведенных на рис. 14.7, не допускает существования оптимума (максимума или минимума). Если по смыслу задачи ожидается наличие экстремума (оптимума), то следует применять трехпараметрические формы связи, например квадратичную модель. Квадратичная модель с функциональными преобразованиями переменных способна описывать довольно широкий класс зависимостей с экстремумами.

Вопросы для самопроверки

1.Сформулируйте задачу регрессионного анализа.

2.Что такое линия регрессии и уравнение регрессии?

3.Что такое сопряженные уравнения и линии регрессии?

4.В чем заключается принцип наименьших квадратов?

5.Как составляется система нормальных уравнений?

6.Что такое коэффициент детерминации?

7.Чем коэффициент детерминации отличается от индекса детерминации? Перечислите их свойства.

8.Опишите наиболее распространенные двухпараметрические нелинейные зависимости.

9.Как графически проверить правильность выбора формы связи?

154

15. Проблема значимости и адекватности регрессионной модели

Оценка значимости регрессионной модели

В регрессионной модели «полный сигнал» – наблюдаемые значения у – разлагается на две компоненты: «полезный сигнал» – расчетные значения ур , которые определяются моделью (значениями аргументов х1 , х2), и «помеху» – ошибки модели е:

у = ур + е,

где, например, yp = b0 + b1x1 + b2x2 для двухфакторной линейной модели.

В лекции 14 об основах регрессионного анализа было показано, что точно такое же разложение имеет общая сумма квадратов отклонений

SSy = SSp + SSe.

Покажем, что такое же разложение имеет также число степеней свободы

dfy = dfp + dfe:
dfy = n – 1, так как на n отклонений	yi y наложена одна связь – сумма
всех этих отклонений равна нулю y y	0 (центральное свойство среднего);

dfе = n – 1 – m, где m – число объясняющих переменных. Для определения параметров модели принимаются условия ортогональности ошибок к каждому члену модели [e] = 0, [ex1] = 0, [ex2] = 0 – это связи, наложенные на отклонения ошибок от их среднего значения. Обычно в модели число определяемых параметров на единицу превышает число аргументов из-за обязательного наличия в модели свободного члена b0 (кстати, наличие в модели свободного члена

приводит к равенству нулю среднего значения ошибки e					0 и равенству сред-
них y p	y ).
Для числа степеней свободы расчетных значений должно получиться:
dfp = dfy – dfe = (n – 1) – (n –1 – m) = m.
Рассмотрим отклонения				расчетных значений от	среднего	значения:
yp y	b0	bj x j y	bj	x j x j . При преобразовании было использова-
но первое уравнение нормальной системы (см. лекцию 14) y b0						bj x j –

следствие условия [e] = 0.

Напоминаем, что в регрессионном анализе все объясняющие переменные xj считаются неслучайными, поэтому оказалось, что все отклонения расчетных

значений от своего среднего yp	y являются разными линейными комбина-
циями m случайных величин bj	с неслучайными коэффициентами x j x j .

155

Отсюда следует, что независимыми могут быть только m таких комбинаций, то есть dfp = m.

Для проверки значимости модели заполним на рис. 15.1 таблицу дисперсионного анализа 1, причем выразим суммы квадратов SSp = R2 SSy и

SSe = (1 – R2) SSy через общую сумму квадратов SSy и коэффициент детерминации R2.

	Источник	Суммы	ЧСС	Средние квад-	Дисперсионное
	изменчивости	квадратов		раты	отношение
	Регрессия	SSp = R2 SSy	dfp = m	MSp = SSp / dfp	Fp = MSp / MSe
	Остаток	SSe =	dfe =	MSe = SSe / dfe
	модели	= (1 – R2) SSy	= n – 1 – m
	Общая	SSy nsx2	dfy = n – 1

Рис. 15.1. Таблица дисперсионного анализа для оценки значимости модели

Получено следующее выражение для дисперсионного отношения Фишера

F

SSp

dfe

R

2

n 1 m

,

p

SSe

dfp

2

1

R

m

которое надо сравнивать

с

табличными

значениями F0,05(dfp; dfe) и

F0,01(dfp; dfe).

Для одномерного случая (m = 1) ЧСС dfp = 1 и дисперсионное отношение

			r 2		n	2
Fp			xy
	1		2	1
			rxy
надо сравнивать с табличными значениями F							1; n 2 t 2 n 2 , где =0,05 и

0,01. Интересно, что для линейной однофакторной зависимости мера тесноты связи rxy и характеристика ее значимости Fp получаются одинаковыми для обеих сопряженных моделей.

Регрессионная модель считается значимой, если вычисленное значение дисперсионного отношения будет больше верхней границы Fp > F0,01 ; модель признается незначимой, если Fp < F0,05 .

Оценка значимости корреляционной связи

Коэффициент детерминации (и коэффициент корреляции) представляет собой меру тесноты связи выбранной формы. Ошибка неверного выбора вида

156

уравнения регрессии (ошибка спецификации модели) может привести к совершенно неверным выводам относительно оценки тесноты реально существующей связи. В некоторых случаях, когда данные опыта даны в нескольких повторениях, можно найти меру чисто случайной изменчивости s2 (дисперсию данных по повторениям – дисперсию «внутри групп»); тогда вычисляют более объективную меру тесноты связи – индекс детерминации (и корреляционное

отношение). В отличие от коэффициента детерминации R2 1					SSe	при вычис-
					SSy
лении индекса детерминации	2	1	SS	не используются никакие предполо-
			SSy

жения о форме корреляционной связи.

Однако параллельные наблюдения (повторения) имеют место только для планируемых опытов (активных экспериментов), что характерно для опытов физических, химических, биологических, там, где исследователь может контролировать условия опыта. В экономике же данные представляют собой наблюдения неконтролируемого процесса (пассивный эксперимент), поэтому варианты опыта почти никогда не повторяются.

Выше уже говорилось, что при понижении шкал измерения теряется ка- кая-то часть информации, но выводы анализа становятся более общими, более объективными. При анализе парных зависимостей полезно перейти к дискретным шкалам измерения обеих переменных, то есть произвести двойную груп-

	пировку данных на несколько небольших интервалов по осям X, Y.
	Если обозначить через Xi и Yj
			X1	X2	X3	…	Xp		l= m	v x y
	центры интервалов, то для каждой
	клетки таблицы размером p q	Y1	m11	m21	m31	…	mp1		l1	v1
	можно подсчитать частоты mij – ко-	Y2	m12	m22	m32	…	mp2		l2	v2
		…	…	…	…	…	…		…	…
	личество наблюдений, попадающих
		Yq	m1q	m2q	m3q	…	mpq		lq	vq
	в данную клетку. Все данные, по-
		k= m	k1	k2	k3	…	kp		n
	падающие в одну клетку таблицы с
		u yx	u1	u2	u3	…	up
	центром (Xi , Yj), считаются одина-
		Рис. 15.2. Корреляционная таблица
	ковыми (это вносит в расчеты неко-

торую ошибку группировки). Сумма всех частот равна общему количеству данных n = mij . Часто такую таблицу называют корреляционной (рис. 15.2).

Теперь суммирование по всем наблюдениям должно учитывать частоты повторения одинаковых данных, например [xy] mijXiYj . Сравнительные расчеты коэффициента корреляции по исходным rxy и по сгруппированным rXY данным дают представление о величине ошибок группировок.

157

Переход к сгруппированным данным позволяет получить дополнительную информацию о форме связи, более объективную меру тесноты существующей корреляционной связи и даже скорректировать наши предположения о возможном направлении причинно-следственных связей. Имея таблицу сгруппированных данных, можно для каждого значения Xi вычислить средние групповые

1

q

q

ui

yxi

mijY j , где ki

mij

– суммы частот по столбцам таблицы. Ана-

k

i

j

1

j

1

логично,

для

каждого

значения

Yj

можно

вычислить средние групповые

1

p

p

v j

xy j

mij X i , где l j

mij

– суммы частот по строкам таблицы.

l

j

i

1

i

1

Теперь появилась возможность для каждой из сопряженных зависимостей

вычислить индексы детерминации:

2

SSU ;

2

SSV ,

y / x

SSY

x / y

SSX

которые показывают, какая часть полной изменчивости результативной переменной объясняется наличием корреляционной связи (произвольного типа, не обязательно линейного). Оба корреляционных отношения превышают абсолютную величину коэффициента корреляции (вычисленного по сгруппированным данным):

y/x , x/y > | rXY |.

Если одно из корреляционных отношений существенно превышает другое, то это является доводом в пользу выбора соответствующего направления причинно-следственных связей.

Кусочно-линейные графики средних групповых (Xi , ui) и (vj , Yj) называются эмпирическими линиями регрессии. Эти графики дают возможность визуально определить вид нелинейности и выбрать более подходящую форму связи, чем традиционная линейная форма, которая часто принимается по умолчанию.

С помощью дисперсионного анализа проверяется значимость наиболее тесной корреляционной связи. Если в результате дисперсионного анализа окажется, что корреляционная связь незначимая, то незачем проводить регрессионный анализ связи заданной формы, она также будет незначимой.

На рис. 15.3 приведена заполненная таблица дисперсионного анализа 2 для проверки значимости корреляционной связи у / х, причем суммы квадратов

SSU = 2 SSY и SS = (1 –		2) SSY выражены через общую сумму квадратов SSY
и индекс детерминации	2	2
		y / x .

158

	Изменчивость	Суммы		ЧСС	Средние	Дисперсионное
		квадратов			квадраты	отношение
	Средние	SSU =	2 SSy	dfU =	MSU = SSU / dfU	F = MSU / MS
	групповые			= p – 1
	Случайность	SS	=	df =	MS = SS / df
		= (1 –	2) SSy	= n – p
	Общая	SSY	ns2	dfy = n – 1
			Y

Рис. 15.3. Таблица дисперсионного анализа для оценки

значимости корреляционной связи

Получено следующее выражение для дисперсионного отношения Фишера:

	SSU	df			2		n	p
F									,
	SS	dfU	1		2		p	1
которое надо сравнивать	с табличными						значениями F0,05(dfU; df ) и
F0,01(dfU; df ).

Если окажется, что F < F0,05 , делаем вывод об отсутствии корреляционной связи (какой-либо формы).

Проверка адекватности модели

Недаром ошибки модели е называются остатками модели, поскольку кроме случайных ошибок, в них включаются систематические ошибки выбора неверной формы связи (ошибки спецификации модели).

Если у нас есть мера чисто случайной изменчивости (дисперсия данных по повторениям опыта), то остатки модели е можно разложить на две компо-

ненты – случайную и систематическую : е = + .
Точно так же разлагается сумма квадратов отклонений	SSe = SS + SS
и число степеней свободы dfe = df + df .
Для проверки значимости систематической ошибки	(ошибки неадек-

ватности модели) заполняем таблицу дисперсионного анализа 3 (рис. 15.4).

Две строки этой таблицы («Остаток модели» и «Случайность») дублируют соответствующие строки таблиц дисперсионных анализов 1 и 2.

Получено следующее выражение для дисперсионного отношения Фишера:

FA	SS		df		2 R2			n	p
										.
	SS		df	1		2		p 1	m

159

	Изменчивость	Суммы		ЧСС	Средние		Дисперсионное
		квадратов			квадраты		отношение
	Неадекватность	SS	=	df =	MS	=	FА =
		= ( 2 – R2) SSy		= p – 1 – m	= SS	/ df	= MS / MS
	Случайность	SS	=	df = n – p	MS	=
		= (1 –	2) SSy		= SS	/ df
	Остаток	SSe =		dfe =	MSe =
	модели	= (1 – R2) SSy		= n – 1 – m	= SSe / dfe

Рис. 15.4. Таблица дисперсионного анализа для проверки адекватности модели

Вычисленное дисперсионное отношение Фишера FA надо сравнивать с

табличными значениями F0,05(df ; df ) и F0,01(df ; df ). Если окажется, что FА < F0,05 , систематической ошибкой можно пренебречь и считать модель адекватной. Но если окажется, что FА > F0,01 , то систематической ошибкой пренебречь нельзя, придется искать более подходящую форму связи.

Пример. На рис. 15.5 в корреляционной таблице приведены результаты двойной группировки данных n = 154 наблюдений; принято р = 7 интервалов равной ширины по переменной Х и q = 6 интервалов равной ширины по переменной Y.

Y	X	1	2	3	4	5	6	7	l= m		mX	V
6		3	0	0	0	0	0	0	3		3	1
5		2	8	3	0	0	0	0	13		27	2,077
4		2	17	4	3	0	1	0	27		66	2,444
3		0	7	20	13	4	0	0	44		146	3,318
2		0	0	4	12	20	5	4	45		218	4,844
1		0	0	0	5	9	6	2	22		115	5,227
k= m		7	32	31	33	33	12	6	154
mY		36	129	99	80	61	20	10
U		5,143	4,031	3,194	2,424	1,848	1,667	1,667
		Рис. 15.5. Корреляционная таблица размером 6								7

При группировках на интервалы равной ширины всегда можно перейти к условным переменным (линейные преобразования переменных) так, чтобы в новых переменных центры интервалов выражались последовательными целыми числами (номерами интервалов). Эти линейные преобразования переменных не изменяют ни последующих выводов анализа, ни вида графиков, у которых будет только другая разметка осей.

160