ТВиМС.Малярец.Егоршин 22.12.12

слово вероятность Р и р, что приводит к некорректным словосочетаниям типа: «Вероятность того, что относительная частота mn отклонится от вероятности р появления события в одном испытании не более чем на , равна удвоенному

значению функции Лапласа с аргументом 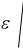pqn ». Это определение громоздко

и малопонятно. Следует избегать в одном предложении двух одинаковых слов, да еще с разным смыслом. Например, вероятность некоторого утверждения

	P	m	p	можно назвать гарантией, надежностью, уровнем доверия. Кста-
		n

ти, вероятность противоположного утверждения называют уровнем значимости и обычно обозначают греческой буквой альфа: = 1 – Р. Если потребуется, то вероятность р появления события в одном испытании можно назвать долей в совокупности, а относительную частоту – долей в выборке. Выражение

	t		pq		называется погрешностью. Теперь теорему можно сформулировать
			n

так: «С уровнем доверия P = 2Ф(t) можно утверждать, что отклонение относи-

тельной частоты

mn

от своей доли в совокупности р (от своего предельного

значения р) не превысит погрешности

t

p 1

p

».

n

Формула P

m

p

t

pq

2

t , или P

m

p

2

n

, свя-

n

n

n

pq

зывает вместе четыре величины n, p, , P. Если в условиях задачи заданы любые три величины, то четвертую можно найти по вышеприведенной формуле. В связи с этим появляется 4 типа задач.

I. Даны n, p, . Требуется найти Р.

Заданы параметры распределения n, p. Дополнительно задана допустимая

	погрешность . Требуется найти уровень доверия утверждения							m	p	, как
								n
	часто оно будет выполняться.
	Решение. Из выражения для погрешности	t		p 1 p			находим t и вы-
				n

числяем уровень доверия (гарантию) P = 2Ф(t).

51

Пример. В процессе статистических испытаний монету предполагается подбросить n = 100 раз. Можно ли утверждать, что в результате опыта отклонение относительной частоты от своего теоретического значения р = 0,5 (то есть погрешность ) не превысит 0,01?

	Определим уровень доверия утверждения					m	0,5	0,01. Из выражения
						n
	0,01 t		0,5 0,5		получим t = 0,2 и далее по	таблицам Лапласа найдем
			100

P = 2Ф(0,2) = 2 0,079 = 0,158. Уровень доверия 15,8 % явно не достаточен, чтобы гарантировать выполнение заданного условия; поскольку только в 16 случаях из 100 возможны столь малые отклонения ( = 0,01).

II. Даны n, p, Р. Требуется найти .

Утверждения должны быть надежными со стандартным уровнем доверия 90 % , 95 % или 99 % . Какую предельную погрешность можно ожидать с таким заданным уровнем доверия?

Решение. Из соотношения P = 2Ф(t) при заданном Р по таблицам интегральной функции Лапласа находим t. Далее вычисляем предельную ожидае-

мую погрешность:
t		p 1 p	.
		n

Пример. Предполагается подбросить монету 100 раз. Какую погрешность следует ожидать с гарантией 95 % ?

Из выражения 0,95 = 2Ф(t) с помощью таблиц Лапласа находим

t = 1,96 2. Далее вычисляем	2		0,5 0,5		0,1. Иными словами, при 100 ис-
			100

пытаниях относительная частота может варьировать в довольно широких пределах от 0,4 до 0,6.

III. Даны p, , Р. Требуется найти n.

Погрешность уменьшается с увеличением числа испытаний. Сколько же требуется провести испытаний, чтобы получать надежные и точные прогнозы?

Решение. Из соотношения P = 2Ф(t) при заданном Р находим t. Далее за-

	писываем условие для предельной погрешности				t		pq		, откуда при извест-
							n
			t	2
	ных p, , t находим n:	n pq		.

52

Пример. Сколько раз надо подкинуть монету, чтобы с гарантией 90 % снизить погрешность до 0,05? Иными словами, сколько требуется испытаний, чтобы с гарантией 90 % относительная частота появления герба при бросании монеты не выходила за пределы интервала (0,45; 0,55)?

Из соотношения 0,9 = 2Ф(t) находим t = 1,64. Далее из неравенства

					1,64 2
0,05 1,64		0,5 0,5		определяем n 0,5 0,5			16,42	269 .
		n			0,05

IV. Даны n, P и m/n . Найти р.

В предыдущих задачах были заданы параметры распределения и требовалось предсказать результат опыта (задача теории вероятностей). В задаче IV известен результат опыта, и надо сделать заключение о параметрах распределения (именно в этом и заключается статистический способ определения вероятностей).

Решение. Соотношение P = 2Ф(t) при заданном Р определяет t. Далее за-

писываем условие | m/n – p |						, которое должно выполняться с заданным уров-
нем доверия:	m	p	t		p 1	p		. Из этого неравенства находим р.
	n				n

Пример. В результате 400 бросков монеты относительная частота появления герба получилась равной 0,5. Какие значения параметра р согласуются с такими результатами опыта? Заключение должно иметь 90-процентный уровень доверия.

Из соотношения 0,9 = 2Ф(t) находим t = 1,64. Далее выписываем неравен-

p 1

p

, возводим его в квадрат и преобразуем:

ство

0,5

p

1,64

400

(0,5 – р)2

0,0822 р(1 – р); 1,0067 р2 – 1,0067 р + 0,25

0;

отсюда р1

р

р2 ,

где р1 , р2

– корни квадратного трехчлена р1,2 = 0,5

0,041.

Итак, по результатам опыта можно сделать заключение, что с гарантией

90 % искомая вероятность р находится в пределах интервала 0,46

р

0,54.

В

заключение

заметим,

что основная

асимптотическая

формула

P m1 m

m2

tm

tm

дает достаточно точные значения лишь для

2

1

больших n > 100.

53

Причина этого заключается в слишком неточной замене интегральной

	m2	m	2	im
					2
суммы интегралом P m1 m m2	P m m		P m dm
	m m1	m		t	m
			1
					1

t dt с теми

же самыми пределами интегрирования. На рис. 5.4 изображен полигон распре-

деления	Лапласа	для	n = 10,
p = 0,3	(локальная		формула
Лапласа	является	достаточно
точной	аппроксимацией		распре-

деления Бернулли даже для небольших значений n). Пусть тре-

буется вычислить	Р(2 m	6) =
= P(2) + P(3) + P(4) + P(5) + P(6)=
= P(m). Так как	m = 1,	то
Р(2 m 6) = P(m) m.

Это площадь столбиковой фигуры (рис. 5.4) с границами

(m1 – 0,5) и (m2 + 0,5), поэтому более правильным будет замена

Рис. 5.4. Аппроксимация распределения

Лапласа столбиковой фигурой

интегральной суммы интегралом, пределы которого несколько шире, чем в общепринятой формуле:

m	2	0,5	tm	0,5
			2
P m1 m m2		P m dm
m1		0,5	tm1	0,5

t dt	tm	2	0,5	tm 0,5 .
				1

Так, для данного примера n = 10,	p = 0,3	точное значение	Р(2 m 6),
рассчитанное по формулам Бернулли,	равно	P(m) = 0,840; по	стандартной

формуле Лапласа – Ф(t6) – Ф(t2) = 0,736 (погрешность 12,4 %); по уточненной формуле – Ф(t6,5) – Ф(t1,5) = 0,842 (погрешность всего 0,2 %).

Доказательство локальной теоремы Лапласа

При преобразовании формулы Бернулли	P m	n!			pmqn m для
	n	m! n	m !

больших значений n > 30 использована асимптотическая формула Стирлинга

				n n		, которая дает тем более точные значения, чем больше n. Но даже
	n! 2 n
				e

для сравнительно небольших значений n эта формула дает уже достаточно хорошие приближения факториалов.

54

Например, для n = 3 точное значение 3! = 6, а по формуле Стирлинга получается 5,84 (погрешность 2,7 %); для n = 6 точное значение 6! = 720, а по формуле Стирлинга – 710,1 (погрешность 1,4 %); для n = 12 точное значение 12! = 479 001 600, а по формуле Стирлинга – 475 691 882 (погрешность 0,7 %).

q

Запишем m

np

t

npq

np 1

t

, тогда

n

m

nq t npq

np

q

p

n

m

nq

t

npq

шем m

np t npq

np 1

t

, тогда

nq 1 t

.

np

nq

Преобразуем формулу Бернулли для n > 1 (np, nq > 5):

P

m

2 n

n

n

e

m

e

n

m

pm

qn m

n

2 m

2

n

m

e

m

т m

m

1

n

np

m

2

np 1 t

q

nq 1

t

p

np

np

1

m

n

m

1

t

q

1

t

p

np

np

2 npq

nq n m

n m

1

exp

m ln 1

t

q

exp

n m

ln 1

t

p

np

np

2

npq

1

q

q

p

p

exp

np 1 t

ln 1 t

nq 1

t

ln 1 t

.

np

np

np

np

2

npq

Преобразуем выражение под знаком экспоненты, используя известное

разложение логарифма ln 1

	2		3 :
		O
	2

np 1

t

q

ln 1

t

q

nq 1

t

p

ln 1 t

p

np

np

nq

nq

2

2

q

q

1

q

p

p

1

p

np 1 t

t

t

nq 1 t

t

t

np

np

np

np

np

2

np 2

t 2

t 2

.

2

2

Окончательно получаем:

Pn

m

n!

p

m

q

n m

1

exp

t 2

t

,

m! n m !

2

2

npq

m

где t

m

np

m a ,

t

1

exp

t

2

.

2

npq

2

m

55

Вопросы для самопроверки

1.Сформулируйте локальную теорему Лапласа, укажите область применения распределения Лапласа.

2.Перечислите особенности дифференциальной функции Лапласа.

3.Перечислите особенности интегральной функции Лапласа.

4.Сформулируйте интегральную теорему Лапласа.

5.Приведите вариант интегральной теоремы Лапласа для симметричных отклонений случайной величины от своего центра.

6.Сформулируйте третью форму интегральной теоремы Лапласа.

7.Перечислите задачи, которые решаются с помощью третьей формы интегральной теоремы Лапласа.

8.Как определить потребное число испытаний, чтобы получать точные и надежные прогнозы?

6. Непрерывная случайная величина

Значения непрерывной случайной величины сплошь заполняют некоторый интервал, поэтому их невозможно перечислить и задать такую случайную величину рядом распределения.

Универсальным способом задания случайной величины является функ-

ция распределения (или интегральная функция распределения):

F(x) = P(X x) – вероятность того, что случайная величина X примет значение, не меньшее заданного х. Для дискретной случайной величины эта функция называется кумулятой и представляет собой функцию накопленных вероятно-

стей F(xj)= p1 + p2 + … + pj .

Из определения функции F(x) следует, что 0 F(x) 1 (так как F(x) – вероятность); F(– ) = P(X – ) = 0 (невозможное событие); F( ) = P(X ) = 1 (достоверное событие). Покажем, что функция распределения неубывающая. Действительно, из рис. 6.1 следует, F(x2) = P(X x2) = P(X x1) + P(x1 < X x2) = = F(x1) + P(x1 < X x2) F(x1) для x2 > x1 (иными словами, большим значениям аргумента соответствуют не меньшие значения функции распределения).

56

Рис. 6.1. Интервалы изменения переменной х

Фактически в общем виде доказали интегральную теорему:

	P(x1 < X x2) = F(x2) – F(x1):
вероятность	попадания случайной величины в полуоткрытый интервал
x1 < X x2	равна разности значений функции распределения на краях этого

интервала (или она равна приращению функции распределения на этом интервале).

Для дискретной случайной величины график функции распределения ступенчатый со скачками – конечными приращениями рi (разрывами 1-го рода) в значениях xi дискретной случайной величины. Для непрерывной случайной величины функция распределения непрерывная, ее график не имеет разрывов. Для непрерывной функции малым приращениям аргумента соответствуют ма-

лые приращения функции: lim

F

0 .

x

x

0

Отсюда следует, что для непрерывной случайной величины вероятность

появления любого ее конкретного значения равна нулю:

P X x lim

P x X

x

x

lim

F x X

x

x F x

lim

F x

0.

x

x

x

x

0

x

0

x 0

Поэтому для непрерывной случайной величины эквивалентны следую-

щие записи интегральной теоремы:

P(x1 < X x2) = P(x1

X < x2) = P(x1 < X < x2) = P(x1

X x2) = F(x2) – F(x1).

Кроме функции распределения F(x), для описания непрерывной случайной величины вводят еще одну функцию – плотность вероятности – отношение вероятности попадания случайной величины в заданный интервал к длине этого интервала. В определении этой новой функции для конкретного значения х используется предельный переход:

f x lim		P x X	x x	.
x	0		x

57

Преобразуем это выражение:

f x lim

P x X

x x

lim

F x

x F x

lim

F x

dF

F .

x

x

x

dx

x

0

x

0

x 0

Функция плотности вероятности f(x) оказалась равной производной от функции распределения F(x), поэтому функцию f(x) называют также дифференциальной функцией распределения.

Наоборот, функция распределения F(x) выражается как интеграл от функции плотности вероятности:

	x
F x	f s ds ,

поэтому функцию F(x) называют также интегральной функцией распределения.

Замечания: в интегральном представлении функция распределения является функцией верхнего предела определенного интеграла, поэтому переменная интегрирования обозначена другой литерой. Нижний предел принят – , чтобы не требовалось добавлять постоянную интегрирования.

Ранее была сформулирована интегральная теорема Лапласа, согласно которой (для конкретного распределения Лапласа) получено выражение:

P m1 m m2	tm	tm ,
	2	1

которое очень напоминает общую интегральную теорему. Вопрос: является ли интегральная функция Лапласа Ф(t) интегральной функцией распределения? Ответ – нет, не является, поскольку значения Ф(t) могут быть отрицательными Ф(–t) = –Ф(t). С помощью интегральной теоремы Лапласа можно найти функцию распределения F(m) = P(X m) = P(– < X m) = Ф(tm) – Ф(– ) = = Ф(tm) + Ф( ) = Ф(tm) + 0,5, то есть интегральная функция распределения Лапласа и интегральная функция Лапласа отличаются постоянным слагаемым 0,5.

Это объясняется тем, что в определении интегральной функции Лапласа нижний предел интегрирования был принят равным нулю, а не – :

		t		1		t	s 2
							2 ds .
	t	s ds				e
				2
		0			0

это было для того, чтобы можно было воспользоваться симметрией – нечетностью функции Ф(t).

58

Функция плотности вероятности неотрицательная f(x) 0 как производная от неубывающей функции распределения F(x). Площадь под дифференциальной кривой равна единице:

f x dx F

1 .

Это свойство используется при решении задач, так как обычно дифференциальная функция задается с точностью до постоянного сомножителя, который подлежит определению.

Площадь под частью дифференциальной кривой на интервале (х1 , х2) равна вероятности попадания случайной величины в этот интервал (рис. 6.2):

x2	x2	x1
f s ds	f s ds	f s ds
x1

Рис. 6.2. Вероятность попадания

случайной величины в интервал

F x2 F x1 P x1 x x2 .

Пример. Равномерный закон распределения. По закону равномерной плотности распределены ошибки округления чисел, время ожидания транспорта, который ходит через равные интервалы времени, место остановки тела под воздействием сухого трения.

Пусть случайная величина распределена на интервале [a, b] с постоянной плотностью вероятности:

0, x a

f x C, a x b .

0, x b

Требуется найти константу С и составить интегральную функцию распределения F(x).

Фигура под дифференциальной кривой равномерного распределения представляет собой прямоугольник с основанием (b – a) и высотой С. Его пло-

	щадь равна С (b – a) = 1, откуда C		1	.
		b	a

Дифференциальная функция задана тремя разными выражениями на трех интервалах, поэтому рассмотрим выражения интегральной функции на этих же интервалах.

59

x

При х < a

f(x) = 0

и

F x

0ds

0 .

При a < x

b f(x) = C и

a

x

ds

x

a

.

F x

0ds

a b

a

b

a

При x > b

f(x) = 0

и

a

b

ds

x

b

a

1.

F x

0ds

0ds

a b

a

b

a

b

Запишем полученные формулы в компактном виде:

		0,		x	a
F x	x	a	,	a	x b .
	b	a
		1,		x	b

Графики дифференциальной и интегральной функций равномерного распределения изображены на рис. 6.3.

Найдем вероятность попадания случайной величины в интервал с гра-

ницами (х1 , х2), где х1 = 0,7 a + 0,3 b ,

х2 = 0,3 a + 0,7 b. Так как оба значения (х1 ,

Рис. 6.3. Равномерный закон

х2) (a, b), то

Р(х1	x х2) = F(х2) – F(х1) =	0,3a	0,7b a		0,7a	0,3b a	= 0,4.
		b	a		b
						a

Чтобы найти математическое ожидание, заметим, что произведение f(x) x означает вероятность попадания случайной величины в малый интервал шириной x в окрестности точки х. Тогда получаем расчетную формулу математического ожидания для непрерывной случайной величины:

M	x	lim	x f x	x	x f x dx .
		x 0
Так же рассчитываются другие моменты распределения, например мате-
матическое ожидание	квадрата		(момент	2-го	порядка) M x2	x2 f x dx .

Дисперсию вычисляем обычным образом:

D(x) = M(x2) – M2(x).

60