11.1.3. Лекция 3. Тема. Общая постановка задачи оптимального автоматического управления

При заданных ограничениях на управляющие воздействия , управляемые величины, а также заданных уравнении объекта управления, критерии опитмальности

J = J(x, и, t) и краевых условиях х(0) и х(Т) необходимо определить оптимальное управление u°(t) и оптимальную траекторию x°(t) или оптимальный алгоритм управления u°= и(х, t), обеспечивающие экстремум заданного критерия оптимальности.

Решение первой задачи приводит к разомкнутой САУ (рис. 1, а), решение второй - к замкнутой САУ (рис. 1, б), в которых АУУ - автоматическое управляющее устройство.

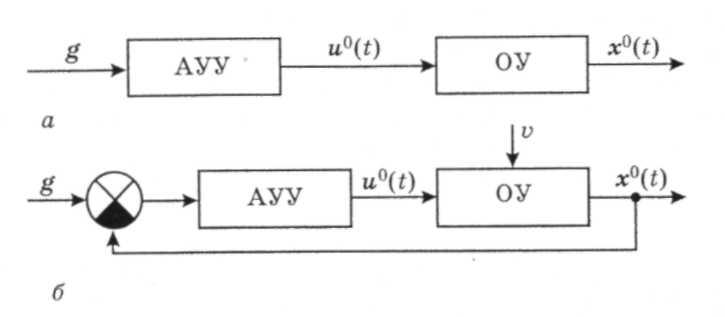
Рис. 1

Для решения задач оптимального управления применяются следующие методы оптимизации: Эйлера-Лагранжа, динамичес-кого программирования Р. Беллмана, нринцип максимума Л.С. ІІонтрягина.

Задача на безусловный экстремум функционала

Эту задачу отличает отсутствие всяких ограничений, что является недостатком, так как отсутствие ограничений обычно лишает задачу практического. Итак, задан минимизируе-мый функционал

Подынтегральная функция Ғ в нем дифференцируема как по х, так и по .

Требуется найти экстремаль x°(t), которая минимизирует данный функционал призаданных краевых условиях х(0), х(t) и известном значении времени Т.

Идея вывода расчетного уравнения использует предположение о том, что к экстремали добавляется дополнительная функция ŋ(t) с весовым коэффициентом α. В результате аргумент функционала получает вариацию и будет равен:

где ŋ(t) - дифференцируемая функция с нулевыми краевыми зна-чениями, т. е. ŋ(0) = ŋ(Т)= 0 (рис.2).

Соответственно функционал получает положительное приращение (вариацию), являющееся функцией коэффициента α:

Эта функция имеет экстремум - минимум при α = 0 (рис 3). Исследуя эту функцию на экстремум, Эйлер получил следующее дифференциальное уравнение для нахождения экстремалей:

Рис. 2 Рис. 3

Компактная условная запись этого уравнения имеет вид:

,

где индексы обозначают производные пo х и x’.

Уравнение Эйлера в общем случае является нелинейным уравнением второго порядка, общее решение которого содержит две постоянные интегрирования, определяемые из краевых условий.

В задаче на безусловный экстремум может быть задан функционал, зависящий от нескольких функций и их первых производных:

В этом случае необходимо решить систему уравнений Эйлера

В более общем случае функционал может зависеть и от

производных высших порядков. В этом случае вместо уравнений

Эйлера составляют и решают уравнения Эйлера-ГІуассона:

где k - порядковый номер функции; п_к - порядок старшей прокз водной от хк; т - число функций.

Задача на условный экстремум. Метод Эйлера—Лагранжа

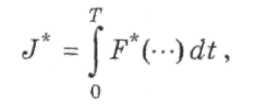
Помимо минимизируемого функционала

подынтегральная функция которого зависит от нескольких функций и их первых производных по времени, задано произвольное чнсло классических ограничений:

Требуется найти n экстремалей при заданных краевых условиях.

Метод решения этой задачи требует формирования нового функционала

где -неизвестные функции, называемые множителями Лагранжа.

Благодаря такой замене задача сводится к предыдущей. При этом уравнения Эйлера должны быть составлены как для искомых экстремалей, так нениями ограничений для множителей. Лагранжа

Поэтому может быть выполнено совместное решение системы уравнений Эйлера (8.1) и заданных ограничений. Исключая время из уравнений экстремалей, можно найти алгоритм управления оптималъного автоматического регулятора.-матричной фо:рме:

Тестовые задания для самоконтроля

1.Для решения задач оптимального управления применяются какие методыоптимизации:

А)Эйлера-Лагранжа

Б) динамичес-кого программирования Р. Беллмана

В) нринцип максимума Л.С. ІІонтрягина.

Г) все ответы верны

Д) все ответы неверны

2. Как называется задача, где отсутствуют всякие ограничения?

A) задача на условный экстремум функционала

Б) задача на безусловный экстремум функционала

В) задача экстремум функционала

Г) задача на искусственный экстремум функционала

Д) задача на естественный экстремум функционала

3.В задаче на безусловный экстремум может быть задан функционал, зависящий:

A) от нескольких функций

Б) от их первых производных

В) от нескольких функций и их первых производных

Г) от функции

Д) от функции и производных высших порядков

4. Как называется задача, где задано произвольное число классических ограничений?

A)задача на условный экстремум функционала

Б) задача на безусловный экстремум функционала

В) задача экстремум функционала

Г) задача на искусственный экстремум функционала

Д) задача на естественный экстремум функционала

5. Какой метод используется для решения задач на безусловный экстремум?

A) метод Эйлера-Пуассона

Б) метод Эйлера- Лагранжа

В) метод Эйлера

Г) метод Лагранжа

Д) метод Риккати