
- •Вопрос 2. Определители 2-го и 3-го порядков. Свойства определителей.
- •Вопрос 3. Миноры и алгебраические дополнения. Вычисление определителей с помощью формул разложения.
- •Вопрос 4. Обратная матрица и её вычисление.
- •Вопрос 5. Ранг матрицы. Вычисление ранга с помощью элементарных преобразований.
- •Вопрос 6. Системы линейных алгебраических уравнений(лау). Матричный способ решения систем лау.
- •Вопрос7. Теорема Кронекера-Капелли о совместности системы лау.
- •Вопрос 8. Формулы Крамера решения систем лау.
- •Вопрос 9 Метод Гаусса решения систем лау.
- •Вопрос 10. Скалярные и векторные величины. Линейные операции с векторами.
- •11. Понятие базиса на плоскости и в пространстве. Ортонормированные базисы на плоскости и в пространстве. Координаты вектора в базисе.
- •12. Скалярное произведение. Координатная форма скалярного произведения.
- •13. Векторное произведение. Координатная форма векторного произведения.
- •14. Смешанное произведение. Координатная форма смешанного произведения.
- •Свойства
- •15. Уравнение прямой (на плоскости), уравнение плоскости, заданных точкой и нормальным вектором.
- •16. Общее уравнение плоскости, общие уравнения прямой в пространстве, общее уравнение прямой на плоскости Общее уравнение плоскости
- •17. Уравнение прямой (на плоскости), уравнение плоскости в отрезках
- •Уравнение прямой в отрезках
- •18. Уравнения прямой на плоскости и в пространстве, проходящей через 2 заданные точки Уравнение прямой, проходящей через две точки
- •19. Уравнение прямой на плоскости и в пространстве, заданной точкой и направляющим вектором Уравнение прямой по точке и направляющему вектору
- •20. Уравнение плоскости, проходящей через 3 заданные точки
- •21. Расстояние от точки до прямой и от точки до плоскости
- •Вопрос 22. Эллипс и его основные свойства..
- •(5) – Каноническое уравнение эллипса с центром в начале координат. Соответственно, уравнение – каноническое уравнение эллипса с центром в точке
- •Вопрос 23. Парабола и её основные свойства.
- •Вопрос 24. Гипербола и её основные свойства.
- •Прямые называются директрисами гиперболы. –левая директриса, – правая директриса.
- •25. Угол между прямыми на плоскости. Условия параллельности и перпендикулярности двух прямых на плоскости.
- •26. Комплексные числа и действия над ними. Действия над комплексными числами
- •27. Тригонометрическая и показательная формы комплексного числа.
- •28. Угол между двумя прямыми в пространстве. Угол между прямой и плоскостью
- •Вопрос29. Понятие квадратичной формы. Знакоопределенность квадратичных форм.
Вопрос 1. Действия с матрицами: умножение на число, сложение, вычитание, умножение матриц. Свойства операций над матрицами.
Прямоугольная
таблица состоящая из m
строк и n
столбцов, элементами которой являются
действительные числа
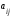 ,
гдеi
– номер
строки, j
- номер
столбца на пересечении которых стоит
этот -элемент, называется числовой
матрицей.
,
гдеi
– номер
строки, j
- номер
столбца на пересечении которых стоит
этот -элемент, называется числовой
матрицей.
А= ,
Матрица обозначается А,В,С… .
,
Матрица обозначается А,В,С… .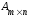 -размер
матрицы.
-размер
матрицы.
Операции над матрицами:
Сложение матрицы. Складывать и вычитать можно матрицы только одинакового размера.
Cуммой этих матриц называется матрица Сmn того же размера, элемент которой находится по формуле
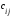 =
=
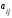 +
+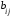 (
(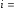 1,m
, j
= 1,n).
1,m
, j
= 1,n).
Пример
1.
Даны две матрицы одинакового
размера.
![]()
Найти сумму А+В двух матриц.
Решение.
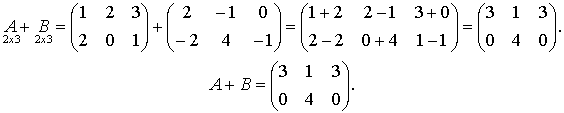
Рассмотрим еще один пример
Пример 2.Пусть даны матрицы:
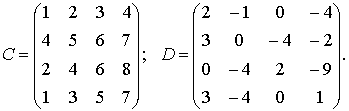
Решение.
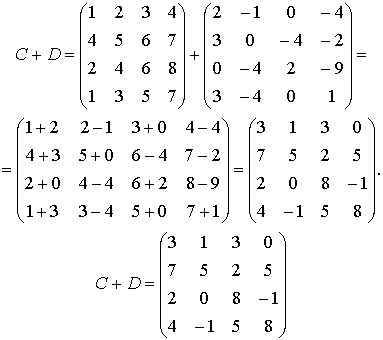
Вычитание
матрицы
=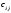
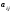 -
-
Умножение
матрицы на число
. Произведением матрицы
Amn×λ
наз-ся число матрицы Bmn=Amn×
λ=
λ×
Amn
элементы
которой
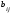 =
λ*
=
λ*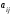 Общий
множитель всех элементов матрицы можно
выносить за знак этой матриц
Общий
множитель всех элементов матрицы можно
выносить за знак этой матриц
Например,
пусть
![]()
Найти результат умножения матрицы А на число 4.
![]()
Умножение
матрицы на матрицу.
Произведением матрицы Аmk
на матрицу Bkn
называется
матрица Cmn
каждый
элемент которой
 равен
сумме произведений элементов і
–ой
(итой) строки матрицы
А на
соответствующие элементы j-го
(житого) столбца матрицы В
, т.е.
Cij=
ai1*b1j+ai2*b2j+…+aik*bkj
═
=
равен
сумме произведений элементов і
–ой
(итой) строки матрицы
А на
соответствующие элементы j-го
(житого) столбца матрицы В
, т.е.
Cij=
ai1*b1j+ai2*b2j+…+aik*bkj
═
=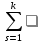 aisbsj
aisbsj
Замечание: Умножать можно только согласованные матрицы. Две матрицы А и В называются согласованными, если число столбцов в первой матрице А равно числу строк во второй матрице В
Пример.
А=
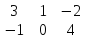 ; В=
; В=
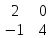
23 22
А×В – не сущ-ет, т.к м-цы А и В не согласованные(3×2)
В × А – согласованные
22 23
В×А
=
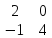 ×
×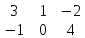 =
=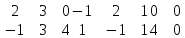
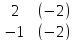
 =
=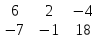
Квадратные матрицы одного порядка всегда согласованные
Транспонирование матрицы. Amn матрица полученная из матрицы А , заменой её строк столбцами без изменения порядка их следования наз-ся транспонированной к матрице А и обозначается Ат
А=
 Ат=
Ат=

23 32
Замечание:
Матрица А называется симметричной,
если А=А ,и
кососимметричной,
если А = –А
,и
кососимметричной,
если А = –А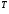 .
.
Возведение матрицы в степень(только для квадратных м-ц) Ап=А*А*А*…*А
Вопрос 2. Определители 2-го и 3-го порядков. Свойства определителей.
Определитель- это число, определяемое по некоторой формуле
Определитель м-цы А обозначается det A или │A│, или ∆. Понятие опред-ля имеет смысл только для квадр-х м-ц.
Опред-м м-цы А первого порядка А= [aij] наз-ся число aij │A│= aij ( А=│5│, │A│=5); (А=│-3│,│A│=-3)
Опред-м м-цы второго порядка А =
 наз-ся
число опред-ое по формуле
наз-ся
число опред-ое по формуле =
=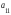
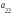 –
–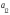
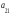
свойства:
Определитель не изменится при замене всех его строк соответствующими столбцами:
 =
= .
.Знак определителя меняется на противоположный при перестановке строк (столбцов) определителя:
 =
–
=
–
 ,
, =
–
=
– .
.
Общий множитель всех элементов строки (столбца) определителя можно вынести за знак определителя:
 =
=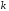
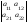 или
или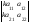 =
=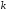
 .
.
Если все элементы некоторой строки (столбца) определителя равны нулю, то определитель равен нулю.
Определитель равен нулю, если соответствующие элементы его строк (столбцов) пропорциональны:
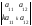 =0,
=0,
 = 0.
= 0.
Если элементы одной строки (столбца) определителя равны сумме двух слагаемых, то такой определитель равен сумме двух определителей:
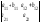 =
= +
+ ,
, =
= +
+ .
.Значение определителя не изменится, если к элементам его строки (столбца) прибавить (вычесть) соответственные элементы другой строки (столбца), умноженные на одно и тоже число
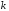 :
:
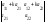 =
= +
+ =
= ,
так как
,
так как =0
по свойству 5.
=0
по свойству 5.
Опред-м м-цы третьего порядка наз. число кот-е вычисляется по формуле
Δ
= =
=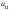
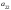
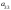 +
+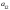
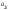
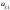 +
+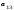
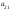
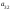 -
-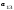
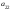
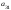 -
-
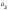
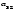 -
-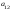
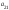
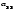 ,
,
Вопрос 3. Миноры и алгебраические дополнения. Вычисление определителей с помощью формул разложения.
Минором Мij элемента aij наз-ся опред-ль,м-цы (n-1)-го порядка полученный из м-цы А вычеркиванием итой строки и житого столбца,
Пример:
А=│
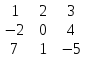 │
;
│
;
М23=│
 │=1*1
- 2*7=13;а23=4.
│=1*1
- 2*7=13;а23=4.
М12=│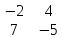 │=
-2*(-5) - 4*7= -18;
а12
= 2.;
М22=│
│=
-2*(-5) - 4*7= -18;
а12
= 2.;
М22=│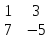 │=
-5-21=26;а22=0.
│=
-5-21=26;а22=0.
Алгебраическим
дополнением элемента
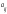 определителя
определителя
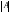 называется его минор
называется его минор ,
взятый со знаком
,
взятый со знаком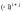 .
Алгебраическое дополнение будем
обозначать
.
Алгебраическое дополнение будем
обозначать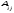 ,
то есть
,
то есть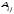 =
=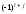 *
* .
.
(8 св-во опред-ля )Теорема Лапласа. Определитель квадратной м-цы А п-го порядка равен сумме всех произведений элементов произвольной строки (столбца) на их алгебраические дополнения
Разложение по эл-там итой строки -│А│=аi1* А i1+ аi2* А i2+…+ аin* А in
Разложение по элементам житого столбца - │А│= а1j * А1j + а2j* А2j +…+ аnj *Аnj
(9
св-во
определителя)
Теорема
аннулирования:сумма
всех произведений элементов одной
строки (столбца) определителя на
соответствующие алгебраические
дополнения элементов другой строки
(столбца) равна нулю, то есть
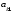
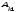 +
+
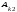 +
+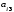
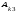 = 0,
= 0,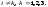
Опред-ль
произведения двух квадратных м-ц равен
произведению определителей этих
квадратных матриц:
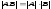
Вопрос 4. Обратная матрица и её вычисление.
Квадратная матрица А порядка n называется новорожденной (неособенной), если её опред-ль не равен 0 ( det A ≠ 0);
в противном случае матрица наз-ся выражденной (особенной) ( det A = 0)
Обратной
м-цей
для
квадратной м-цы А
порядка n
наз-ся
м-ца
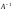 ,
если выполняются равенства
,
если выполняются равенства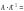
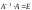 ,
гдеЕ
– единичная матрица того же порядка
n,
что и м-ца А
,
гдеЕ
– единичная матрица того же порядка
n,
что и м-ца А
Теорема: Необходимое и достаточное условие существования м-цы. Для того, чтобы квадр-я м-ца А имела обратную, необходимо и достаточно, чтобы она была выражденной.
Алгоритм нахождения обратной матрицы:
Вычисляем опред-ль м-цы А. Если опред-ль м-цы А = 0, то обратной м-цы не сущ-ет. Если А≠0, то
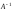 сущ-ет.
сущ-ет.Строим м-цу
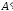 составленную
из алгебраических дополнений к м-цеА :
составленную
из алгебраических дополнений к м-цеА :
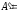
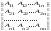 .
.
3)
Строим присоединительную м-цу
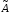 к м-це
к м-це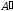 :
: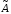 -
(
-
(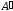 )т=
)т=
 .
.
4)
Находим обратную м-цу по формуле:

Необходимо сделать проверку:
А
*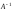 =
Е
=
Е
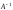 *
А=Е
*
А=Е
Св-ва обратной м-цы
1.
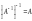 ;
;
2.
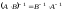 ;
;
3.
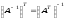 .
.
