Вопрос 5. Ранг матрицы. Вычисление ранга с помощью элементарных преобразований.

Рангом r (A) м-цы А наз-ся макс-ый порядок ее миноров, отличных от нуля. Минором k-го(факториального) порядка м-цы А наз-ся опред-ль k-го(факториального) порядка, построенный из эл-тов м-цы А, находящихся на пересечении k строк и k столбцов м-цы А. Базисным минором м-цы наз-ся всякий отличный от нуля минор, порядок кот-го = рангу данной м-цы. Ранг м-цы = 0 тогда, когда А – нулевая м-ца.

Пример: Определить ранг матрицы А=

Решение: Матрица А имеет порядок 3×4 , следовательно, ранг матрицы 0 ≤ r (A) ≤ 3. Для опред-ния ранга вначале найдем все возможные миноры 3-го порядка: если хотя бы один из них отличен от нуля, значит, ранг м-цы А равен трем. Всего имеем 4 минора 3-го порядка: ,,,

Т. к. достаточно найти среди них хотя бы один, отличный от нуля, то выберем тот минор, который содержит большее кол-во нулевых элементов:=1*(-1)³⁺² r(A) 3..

Данный минор будет являться базисным для исходной м-цы.Если бы все приведенные в примере миноры 3-го порядка оказались =-ми 0, то это привело бы к рассмотрению миноров 2-го порядка. В этом случае ранг м-цы был бы меньше трех. М-цы А и В наз-тся эквивалентными (А~В), если одна из них получается из другой с помощью элементарных преобразований.

К элементарным преобразованиям относят:

1) перестановку местами любых двух строк (столбцов) матрицы;

2) умножение каждого элемента строки (столбца) на один и тот же множитель λ ≠ 0;

3) прибавл-ие (выч-ие) к эл-там строки (столбца) соотв-щих эл-тов другой строки (столбца), умнож-х на один и тот же множитель.

Ранги эквивалентных м-ц совпадают, т.е. ранг м-цы не меняется, если к м-це применить элементарные преобразования 1-3. Если хотя бы один эл-нт м-цы А 0, то ранг м-цы больше нуля. Таким образом, ранг является еще одной важной характеристикой матрицы.Имеют место следующие утверждения:

1) если ранг м-цы А = k, то сущ-ет ровно k линейно-независимых строк (столбцов), от кот-х линейно зависят все остальные строки (столбцы), т. е. все остальные строки выражаются ч-з эти k линейно-независимых строк;

2) макс-е число линейно-независ-х строк м-цы совпадает с макс-ым числом линейно-независ-х столбцов и = рангу м-цы.

Вопрос 6. Системы линейных алгебраических уравнений(лау). Матричный способ решения систем лау.

Системой m линейных алгебраических уравнений с n неизвестными x₁ , x₂ , ... , x_n называется система вида:

₍₁₎ Данная система может быть записана в матричном виде АХ = В , (2)

где А = есть м-ца сис-мы(1), или м-ца коэф-тов;

Х = есть м-ца-столбец неизвестных; В = есть м-ца- столбецсвободных членов.

Если В = 0, то система (1) называется однородной, если же В ≠ 0, то неоднородной.

Решением сис-мы (1) наз. всякая совокупность чисел , кот-я, будучи подставленной в сис-му, превращает каждое ее урав-ние в тождество. Однако не каждая сис-ма ЛАУ имеет решение. Если не сущее-ет ни одной совокупности значений, удовлетворяющей заданным урав-ям сис-мы, то сис-ма(1) наз несовместной. В противном случае, сис-ма (1) наз совместной. Совместная сис-ма может иметь единственное реш-ие, или бесконечное множ-во реш-й.

Матричный м-д решения систем ЛАУ. Если в сис-ме (1) m=n и detA ≠ 0 (м-ца невырожденная), то для неё сущ-ет обратная м-ца . Умножим обе части равенства(2) слева на 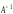: ×А×Х=×В Е×Х=×В, отсюда Х = 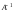×В. (3) Формула (3) явл-ся матричной записью реш-я сис-мы ЛАУ. Т. к. обратная м-ца единственная, то сис-ма (1) имеет единственное реш-е. Таким образом для реш-я сис-мы ЛАУ матрич-м м-дом необх-мо найти обратную м-цу к м-цеА и умножить её слева на столбец свободных членов В

Правило Крамера: Если м-ца А сис-мы ЛАУ не выражденная, то сис-ма имеет единственное реш-е полученное по формулам:

Х_{i =} , где ∆-опред-ль м-цы А ; ∆_i -опред-ль получ-й из опред-ля м-цы А заменой i-го столбца на столбец свободных членов В

М-д Гаусса: Этот м-д можно использ-ть для реш-я любых сис-м ЛАУв том числе и тех, у кот-х число урав-ний ≠ числу неизвестных(т ≠ п)