
- •Глава IV Теория случайных процессов
- •Тема 16. Основы теории случайных процессов
- •1. Понятие случайной функции, стохастические процессы
- •2. Процесс Пуассона
- •3. Классификация случайных процессов
- •4. Математическое ожидание и дисперсия случайного процесса
- •5. Корреляционная функция случайного процесса
- •5.1. Нормированная корреляционная функция
- •5.2. Взаимная корреляционная функция случайного процесса
- •6. Стационарный случайный процесс в широком и узком смысле
- •7. Линейные и нелинейные преобразования случайных процессов
- •8. Дифференцирование и интегрирование
- •9. Элементы спектральной теории стационарных
- •9.1. О дисперсии стационарного случайного процесса.
- •9.2. Дискретный спектр, с произвольным конечным числом частоты.
- •10. Спектральная плотность случайного
- •11. Стационарный белый шум, дельта функция
- •Тема 17. Марковские случайные процессы
- •1. Понятие Марковской цепи, марковские случайные процессы
- •2. Дискретный Марковский процесс, цепь Маркова
- •3. Примеры Марковских цепей
- •4. Расчет цепи Маркова для стационарного режима
- •5. Понятие о непрерывном Марковском процессе,
2. Дискретный Марковский процесс, цепь Маркова
Пусть в некоторой системе
![]() происходит с.п. с дискретными состояниями
происходит с.п. с дискретными состояниями![]() и дискретным временем, т.е. переход
системы из одного состояния в другое
происходит только в определённые моменты
времени
и дискретным временем, т.е. переход
системы из одного состояния в другое
происходит только в определённые моменты
времени![]() .
Эти моменты называютшагами процесса
(обычно разности смежных моментов
наблюдения
.
Эти моменты называютшагами процесса
(обычно разности смежных моментов
наблюдения![]() равны
постоянному числу – длине шага,
принимаемого в качестве единицы времени);
равны
постоянному числу – длине шага,
принимаемого в качестве единицы времени);![]() начало
процесса.
начало
процесса.
Этот с.п. можно рассматривать как
последовательность (цепь) событий
![]() .
.
![]() начальное
состояние системы, т.е. перед 1-м шагом;
начальное
состояние системы, т.е. перед 1-м шагом;![]() состояние
системы после 1-го шага,
состояние
системы после 1-го шага,![]() состояние
системы после 2-го шага и т.д.), т.е. событий
вида
состояние
системы после 2-го шага и т.д.), т.е. событий
вида![]() где
где![]() .
.
Марковский случайный процесс с дискретными состояниями и дискретным временем называют марковской цепью(цепь Маркова).
Отметим, что марковский цепь, в которой условные вероятности состояний в будущем зависят только от состояния на последнем этапе (и не зависят от предыдущих), называютпростой цепью Маркова. (А.А. Марков 1856-1922- русский математик).
Примером такой системы
![]() может
служить техническое устройство, возможные
состояния которого следующие:
может
служить техническое устройство, возможные
состояния которого следующие:
![]() исправная
работа;
исправная
работа;
![]() профилактический
осмотр и обслуживание;
профилактический
осмотр и обслуживание;
![]() ремонтная
работа;
ремонтная
работа;
![]() списание
за негодностью;
списание
за негодностью;
Граф состояние работы изображен на рисунке
Рис. 1.11.(А.А. Белов, и др.)
Из анализа графа видно, что из состояния
нормальной работы вершины
![]() система может переходить в состояние
профилактического обслуживания
система может переходить в состояние
профилактического обслуживания![]() ,
а затем опять возвращаться в
,
а затем опять возвращаться в![]() .
Или переходить из
.
Или переходить из![]() в
состояние ремонта
в
состояние ремонта![]() ,
после чего либо возвращается в
,
после чего либо возвращается в![]() ,
либо переходить в состояние списания.
Состояние
,
либо переходить в состояние списания.
Состояние![]() является
конечным, так как переход из него
невозможен. Переход из
является
конечным, так как переход из него
невозможен. Переход из![]() опять
в
опять
в![]() означает
задержку в этом состоянии.
означает
задержку в этом состоянии.
На практике часто встречаются системы,
состояния которых образует цепь, в
которой каждое состояние
![]() (кроме
крайних
(кроме
крайних![]() и
и![]() )
связано прямой и обратной связи с двумя
соседними,
)
связано прямой и обратной связи с двумя
соседними,![]() а крайние состояния – с одним соседним
(см. рис.)
а крайние состояния – с одним соседним
(см. рис.)
Рис.1.12(Белов…)
Примером такой системы может служить
техническое устройство, состоящее из
однотипных узлов. Каждое состояние
системы характеризуется числом
неисправных
![]() узлов
в момент проверки.
узлов
в момент проверки.
Основной задачей исследования является
нахождение вероятностей состояния
![]() на
любом
на
любом![]() м
шаге. Будем вычислять вероятности
состояний дискретной системы
м
шаге. Будем вычислять вероятности
состояний дискретной системы
Мы здесь будем рассматривать только простые цепи Маркова. Далее, кратко будем также рассматривать понятия о непрерывных Марковских процессах.
При дискретном времени изменения состояний системы каждый переход от одного состояния к другому называют шагом.
Из определения марковской цепи следует,
что для нее вероятность перехода системы
![]() в
состояние на
в
состояние на![]() м
шаге зависит только от того, в каком
состоянии
м
шаге зависит только от того, в каком
состоянии![]() находилась
система на предыдущем
находилась
система на предыдущем![]() шаге.
шаге.
![]() .
.
где
![]() безусловная
вероятность того , что на
безусловная
вероятность того , что на![]() м
шаге система именно будет находиться
в состояние
м
шаге система именно будет находиться
в состояние![]() .
Для нахождения этих вероятностей
необходимо знать начальное распределение
вероятностей
.
Для нахождения этих вероятностей
необходимо знать начальное распределение
вероятностей![]() т.е. вероятности состояний
т.е. вероятности состояний![]() в
момент времени
в
момент времени![]() (начало
процесса) и так называемыепереходные
вероятности
(начало
процесса) и так называемыепереходные
вероятности
![]() марковской цепи на
марковской цепи на![]() м
шаге.
м
шаге.
Переходной вероятностью
![]() называют
условную вероятность перехода системы
называют
условную вероятность перехода системы![]() на
на
![]() м
шаге, в состояние
м
шаге, в состояние![]()
![]()
![]() м
шаге она была в состоянии
м
шаге она была в состоянии![]() ,
т.е.
,
т.е.
(43)
![]() ,
,
где первый индекс указывает на номер предшествующего, а второй индекс на номер последующего состояния системы.
Цепь Маркова называется однородной,
если величина,![]() т.е.
условные вероятности
т.е.
условные вероятности![]() не
зависят от номера испытаний, в противном
случае называется неоднородной.
не
зависят от номера испытаний, в противном
случае называется неоднородной.
Далее, мы будем рассматривать только
однородные цепи, которые могут быть
заданы с помощью вектора
![]() -
вероятности состояний в момент времени
-
вероятности состояний в момент времени![]() и матрицы (называемой матрицей перехода)
и матрицы (называемой матрицей перехода)
(44)
 .
.
Элементы матрицы
![]() обладают основными свойствами обычных
квадратных матриц и дополнительно
следующими свойствами:
обладают основными свойствами обычных
квадратных матриц и дополнительно
следующими свойствами:
а)
![]() ,
б)
,
б)![]() при
каждом фиксированном
при
каждом фиксированном![]() ,
т.е. сумма элементов каждой строкиматрицы переходаравна единице (как
вероятности событий перехода из одного
состояния
,
т.е. сумма элементов каждой строкиматрицы переходаравна единице (как
вероятности событий перехода из одного
состояния![]() в любое другое возможное состояние
в любое другое возможное состояние![]() -
образующих полную группу событий).
-
образующих полную группу событий).
Вероятность состояния системы на следующем шаге определяется по рекуррентной формуле:
![]()
При некоторых условиях (эргодичность, однородность, отсутствие циклов) в цепи Маркова устанавливается стационарный режим, в котором вероятности состояний системы уже от номера шага не зависят. Такие вероятности называютпредельными(или финальными) вероятностями цепи Маркова:
![]() .
.
Имеет место утверждение.
Теорема 17.1. Для матрицы
перехода вероятностей за
![]() шагов
шагов
![]() справедлива формула
справедлива формула
(45)
![]() ,
,
где![]() .
.
Доказательство. По правилу умножения
двух квадратных матриц![]() го
порядка имеем
го
порядка имеем
![]() где
где![]()
при этом, по определению матрицы перехода
известно, что
![]() при
любом
при
любом![]() .
.
Просуммируем обе части равенства
![]() по
всем
по
всем![]() ,
и заменяя порядок суммирования после
дважды применения свойство а) получим,
что
,
и заменяя порядок суммирования после
дважды применения свойство а) получим,
что![]() матрица
перехода за два шага. Аналогично,
последовательно рассуждая шаг за шагом,
получим наше утверждение в общем случае.
матрица
перехода за два шага. Аналогично,
последовательно рассуждая шаг за шагом,
получим наше утверждение в общем случае.
Пример 3. Задана матрица перехода![]()
 .
.
Найти
матрицы переходных вероятностей
![]() .
.
На основании правила умножения двух матриц получим
 .
.
Задание. Проверьте, что верно равенство
 .
.
Следует отметить, что конечная дискретная цепь Маркова представляет с собой дальнейшее обобщение схемы Бернулли, к тому же на случай зависимых испытаний; независимые испытания являются частным случаем марковской цепи. Здесь под «событием»
понимается состояние системы, а под «испытанием» понимается изменение состояния системы.
Если «испытания» (опыты) являются независимыми, то появление определённого события в любом опыте не зависит от результатов ранее произведённых испытаний.
Задания.а) Заданы матрицы переходов
1.
 ;
;
2.
 ;
;
3.
 .
.
Найти в каждом случае матрицу
![]() .
.
Ответы: а) 1. ;
;
2. ;
;
3.
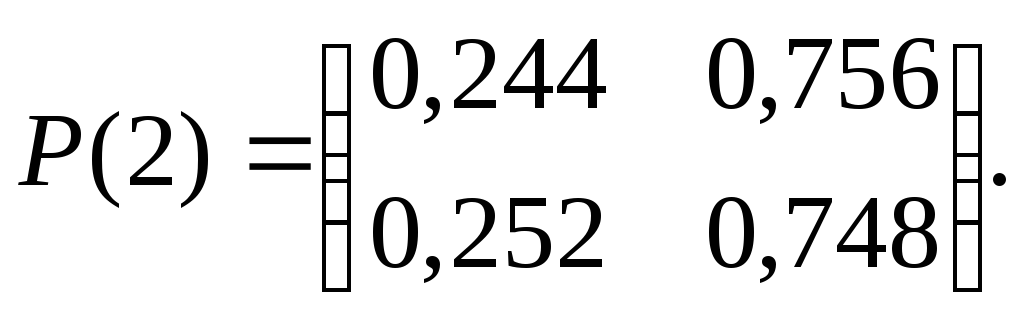
в) Заданы матрицы переходов
 ;
;
 .
.
Найти
![]() .
.
Ответы: в) 1. ;2.
;2. ;
;
3.
 .
.
Замечание. В
общем случае
дискретная
марковская
цепь
![]() представляет
собой марковский случайный процесс,
пространство состояний которого конечно
или счётное, а множество индексов
представляет
собой марковский случайный процесс,
пространство состояний которого конечно
или счётное, а множество индексов![]() -
множество всех неотрицательных целых
чисел или его некоторое подмножество
(конечное или счётное). Мы можем говорить
об
-
множество всех неотрицательных целых
чисел или его некоторое подмножество
(конечное или счётное). Мы можем говорить
об![]() как об исходе
как об исходе![]() го
испытания.
го
испытания.
Часто пространство состояний процесса
удобно отожествить с множеством
неотрицательных целых чисел
![]() и в этих случаях говорят, что
и в этих случаях говорят, что![]() находится
в состоянии
находится
в состоянии![]() ,
если
,
если![]() .
.
Вероятность попасть случайной величины
![]() в состояние
в состояние![]() (называемая одношаговой переходной
вероятностью), как уже было упомянуто
выше, обозначается
(называемая одношаговой переходной
вероятностью), как уже было упомянуто
выше, обозначается![]() ,
т.е.
,
т.е.
(46)
![]() .
.
В таком обозначении подчёркивается, что в общем случае переходные вероятности зависят не только от начального и конечного состояний, но и от момента осуществления перехода.
В случаях, когда одношаговые переходные
вероятности не зависят от временной
переменной (т.е. от значения
![]() ,
то говорят, что марковский процесс
обладаетстационарными переходными
вероятностями. Итак, для дальнейшего
отметим, что имеет место равенство
,
то говорят, что марковский процесс
обладаетстационарными переходными
вероятностями. Итак, для дальнейшего
отметим, что имеет место равенство![]() ,
который не зависит от
,
который не зависит от![]() ,
и
,
и![]() обозначает вероятность перехода за
одно испытание из состояния
обозначает вероятность перехода за
одно испытание из состояния![]() в состояние
в состояние![]() .
.
Обычно вероятности
![]() объединяют
в квадратную матрицу (конечную или
счётную) в зависимости от рассматриваемого
процесса:
объединяют
в квадратную матрицу (конечную или
счётную) в зависимости от рассматриваемого
процесса:
 ,
,
и называют марковской матрицей, или матрицей переходных вероятностеймарковской цепи.
В матрице
![]()
![]() я
строка представляет собой распределение
вероятностей с.в.
я
строка представляет собой распределение
вероятностей с.в.![]() при
условии, что
при
условии, что![]() .
Если число состояний, конечно, то
.
Если число состояний, конечно, то![]() -
конечная квадратная матрица, порядок
которой (число строк) равен числу
состояний.
-
конечная квадратная матрица, порядок
которой (число строк) равен числу
состояний.
Естественно, что вероятности
![]() удовлетворяют
следующим двум условиям:
удовлетворяют
следующим двум условиям:
а)
![]() ,
,
б)
![]() при
каждом фиксированном
при
каждом фиксированном![]()
Условие б) отражает тот факт, что каждое испытание вызывает некоторый переход из одного состояния в другое состояние. Для удобства обычно говорят также о переходеи в том случае, когда состояние остаётся неизменным. Имеет место утверждение.
Теорема 17.2. Процесс полностью определён, если заданы вероятности (46), т.е.
![]() ,
,
и
распределение вероятностей случайной
величины
![]() .
.
Доказательство. Покажем, что для
любого конечного![]() как
вычисляются вероятности
как
вычисляются вероятности
(47)
![]() ,
,
так как по формуле полной вероятности
любые другие вероятности, относящиеся
случайным величинам
![]() ,
могут быть получены суммированием
слагаемых (членов) вида (47).
,
могут быть получены суммированием
слагаемых (членов) вида (47).
По определению условной вероятности имеем
(48)
![]()
![]() .
.
Но по определению марковского процесса получим
(49)
![]()
![]()
Поставляя равенство (49) в (48) получим
(50)
 .
.
Продолжая этот процесс последовательно, получим:
(51)
![]() .
.
Процесс полностью определён. Что требовалась доказать.
