2.3. Сглаживания экспериментальных зависимостей

метод наименьших квадратов (МНК)

Пусть проводится некоторый опыт, целью которого является исследование зависимости определённой физической (экспериментальной) величины от другой (скажем от). Будем предполагать, что величиныисвязаны некоторой функциональной зависимостьюВид этой зависимости и требуется из опыта.

Предположим вначале, что зависимостьизвестна и в результате опыта получен ряд экспериментальных точекОбычно, эти точки не ложатся точно на графике нашей функции. Как правило, имеется некоторый разброс точек, полученных опытным путём от графика нашей функции, т.е. обнаруживается случайные отклонения от данной функциональной зависимости. Эти отклонения связаны с неизбежными допустимыми ошибками при любом опыте. В связи с этим возникает естественный вопрос, «не зная зависимости , как, наилучшим образом воспроизвести эту зависимость по экспериментальным данным».

Простое соединение все экспериментальные точки некоторой кривой линией, являющейся графиком определённой функции, в общем случае лишено смысла. Потому, что вид этой зависимости будет меняться при разных сериях измерений, а в некоторых случаях её в принципе нельзя получать (несколько экспериментальных точек могут иметь одинаковые абсциссы и разные ординаты). В этом случае возникнет типичная задача для практики «задача сглаживания экспериментальных зависимостей», т.е. требуется найти функцию , чтобы она некоторым наилучшим образом отражала функциональную зависимостьот, и вместе с тем были бы сглажены случайные, незакономерные отклонения измерений, связанные с неизбежными погрешностями самых измерений.

Обычно ситуация облегчается тем, что из теоретического соображения или из других соображений, связанных с существом рассматриваемой задачи, и даже по полученному экспериментальному материалу можно указать вид функциональной зависимости от(линейная, квадратичная, показательная и т.д.). Требуется только установить численные значения параметров этих зависимостей. Именно, далее задачу рационального выбора таких числовых параметров будем рассматривать. Ниже дадим кратко обоснование так называемогометода наименьших квадратовна примере нормально распределённых случайных величин.

Итак, пусть имеются результаты независимых измерений - опытные точкиИз теоретических или иных соображений, с точностью до количества (или других признаков) неизвестных параметров (здесь мы ограничимся двумя)иизвестна функциональная зависимостьотв виде

(35) .

Экспериментальные точки уклоняются от этой зависимости вследствие неизбежных ошибок измерений. Как правило, эти ошибки распределены по нормальному закону. Рассмотрим некоторое значение независимой переменной . Результат измерения может рассматриваться как нормально распределённая случайная величинас математическим ожиданиеми соответствующим среднеквадратичным отклонением, характеризующим ошибку измерений. Дополнительно предположим, что «точность измерения во всех точках одинакова, то естьТогда плотность вероятности с.в.имеет вид

(36)

В результате получаем мерную случайную величину, координаты которой независимы и плотности вероятности которых определении равенствами (36). Как было показано ранее, плотность распределения системы независимых случайных величин равна произведению плотностей вероятности компонент:

(37)

Теперь для определения параметров ивоспользуемся идеей метода максимального правдоподобия (ММП), согласно которой в эксперименте реализуются те значения компонент, при которых плотность вероятности системы (37), близка к максимальному значению. Учитывая специальный вид равенств (37), можно заметить, что она достигает максимума, когда показатель степени принимает максимальное значения. Отбрасывая отрицательный множительприходим к задаче отыскания минимума выражения:

(38) .

Поскольку минимизируется сумма квадратов разностей экспериментальных и теоретических значений функции (их обычно называют «невязками»), предложенную процедуру называют методом наименьших квадратов.

Согласно теории дифференциального исчисления в принципе задача сводится к решению

системы двух однородных дифференциальных уравнений в частных производных:

(39)

Если функциональная зависимость (35) линейна относительно параметров и, то система уравнений (39) также будет линейной и её решение можно найти известными методами линейной алгебры.

Таким образом, в общем случае мы приходим к следующему выводу.

Метод нахождения оценки неизвестного параметра, основанный на минимизации суммы квадратов отклонений выборочных данных от определяемой (искомой) оценкиназывается методом наименьших квадратов.

Другими словами, в МНК требуется найти такое значение, которое минимизировало бы сумму

Следует отметить, что МНК является наиболее простым и практичным методом нахождения оценок параметра .

Пример 12.Проведена серия опытов по определению влияния дозы внесённых удобрений

на повышение урожайности некоторой сельхоз культуры (например, пшеницы). Соответствующие данные приведены в трёх столбцах таблицы, и пусть выражает внесённую дозу удобрений в центнерах на гектар,выражает прирост урожайности в центнерах с гектара

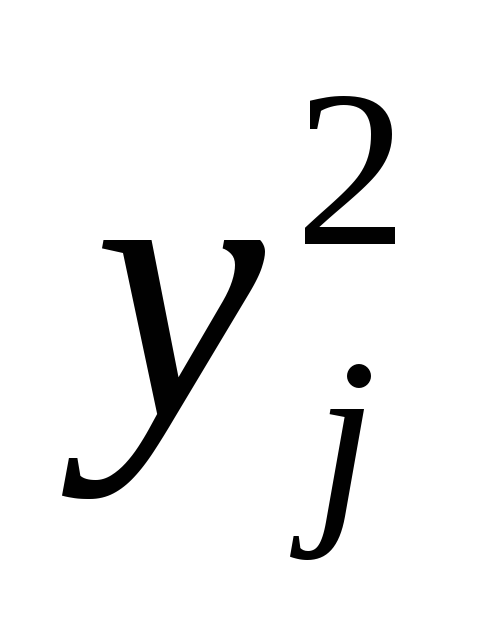
1	0,342	2,10	0,1170	4,41	0,718
2	0,417	4,70	0,1739	22,09	1,960
3	0,675	6,05	0,4556	36,60	4,084
4	0,867	8,65	0,7517	74,82	7,500
5	1,000	10,00	1,0000	100,00	10,000
6	1,158	12,60	1,3410	158,76	14,591
7	1,283	12,08	1,6461	145,93	15,499
8	1,500	14,68	0,2500	215,50	22,020
9	1,733	16,65	3,0033	277,22	28,854
10	2,008	19,25	4,0321	370,56	38,654
11	2,083	19,98	4,3389	399,20	41,618
12	2,242	23,20	5,0266	538,24	52,014
13	2,508	23,93	6,2901	572,64	60,016
	1,370	13,37	2,3405	224,31	22,887

Требуется, применяя метод наименьших квадратов подобрать линейную функцию , выражающуючерез.

Решение. Предполагая, искомые величины связаны между собой линейной зависимостью

. Определим коэффициентыина основании системы (39).

Система (39) в нашем случае принимает вид:

После раскрытия скобок и некоторых стандартных преобразований, для определения наших параметров иполучим следующую систему двух линейных уравнений

Решая эту систему методом последовательного исключения неизвестных (методом Гаусса), в итоге получим:

Замечание. Во многих приложениях также используется и другая зависимость:также линейное относительно параметрови. В этом случае задача легко может быть сведена к предыдущей заменой переменной:

Пример 13. Найдём оценку параметрараспределения Пуассона методом наименьших квадратов.

Решение.Найдём точку минимума функцииНайдём.

Из уравнения находим критическую точку: -2т.е.

следовательно, Поскольку

при любом значении , то

будет точкой минимума функции Таким образом, оценкой параметрав распределении Пуассона

в соответствии с МНК, является величина .

Задание. Докажите, что имеют место равенства:

Задачи с указаниями.

1. Найти оценку параметра распределения Пуассона методом моментов.

Указание. Распределение Пуассонасодержит один параметр.

Для оценки его методом моментов запишем уравнение . Отсюда следует, что

Следовательно,

2. Пользуясь ММП, оценить вероятность, появление герба, если при десяти подбрасываниях монеты герб появился шесть раз.

Указание. В данном случае с.в. является дискретной с законом распределения

	1	0
		1-

Так как

то функция правдоподобия имеет вид: Тогда

и уравнение правдоподобия

3. Пусть случайная величинаравномерно распределена со значениями в отрезке, т.е.. По выборкеоценить величиныиметодом моментов.

Указание. В этой задаче требуется оценить две величиныи, т.е. величиныи, методом моментов. Как было показано ранее, (см. Т. 9.5)Решая систему уравнений

Отсюда находим: т.е.

и, значит,(вариантиз-заисключается). Таким образом, оценки величиниполучены и таковы:

Задание. Решая систему

получить те же самые оценки.

Теперь, кратко остановимся на общий случай, когда рассматриваемая зависимость близка к некоторой функциональной зависимости, где входят семейство параметров больше чем два, т.е. функциональная зависимость имеет общий вид

(40) ,

требуется подобрать значения параметров так, чтобы кривая (40) наименее уклонялась от точек полученных экспериментальным путём.

Решение этой задачи, например, методом наименьших квадратов (МНК) заключается в отыскании таких значений параметров, для которых выражение

(41)

принимает наименьшее значение. И здесь, задачу можно свести к решению системы уравнений

(42)

где число уравнений совпадает с числом неизвестных параметров.

В общем случае решить систему (42) при произвольной функции конечно невозможно; для практического приложения необходимо задаться конкретным видом функции. В ряде случаев функциюзадают в виде многочлена

,

где роль параметров играют коэффициенты . В некоторых случаяхвыбирается как комбинация показательных функций

где какие-то из чисел имогут быть заданы заранее, в то время как другие неизвестны (эти неизвестные и играют роль параметров, подлежащих вычислению). Возможны, разумеется и другие формы задания функции.