fizpr

эта фигура.

6.Пользуясь соотношением (5), вычислить неизвестную частоту второго сигнала.

7.Вычисление выполнить для 7 разных фигур Лиссажу.

8.Рассчитать погрешность определения частоты неизвестного сигнала методом Стьюдента.

Таблица 1 - Результаты измерений и вычислений

№	ν x , Гц	nx	n y	ν y	Форма
п/п					, Гц
					фигуры Лиссажу

1

2

3

4

5

КОНТРОЛЬНЫЕ ВОПРОСЫ

1.Что такое осциллограф? Структурные блоки осциллографа.

2.Из чего состоит электронно-лучевая трубка?

3.Для чего нужен генератор развертки?

4.Для чего используется синхронизация частоты генератора?

5.Что такое фигуры Лиссажу и от чего зависит их форма?

6.Как получить фигуру Лиссажу на экране осциллографа?

7.Как определить частоту неизвестного сигнала?

8.Как получить уравнение траектории точки, которая осуществляет колебания одновременно в двух взаимно перпендикулярных направлениях?

9.Запишите уравнение гармонического колебания и дайте определение его основных характеристик.

121

Лабораторная работа № 402

ИЗУЧЕНИЕ ЗАТУХАЮЩИХ КОЛЕБАНИЙ В КОЛЕБАТЕЛЬНОМ КОНТУРЕ

Цель работы: Исследование зависимости амплитуды затухающих колебаний от времени, определение логарифмического декремента затухания.

Приборы и оборудование: колебательный контур, электронный осциллограф, генератор импульсов, магазин сопротивлений.

Основные требования к теоретической подготовке: При подготовке к лабораторной работе необходимо проработать разделы курса общей физики "Гармонические колебания", "Электромагнитные колебания" и методические указания к данной работе.

Теория метода и описание установки

Электромагнитный колебательный контур состоит из

последовательно соединенных катушки	индуктивности	L	,
конденсатора C и внешнего сопротивления R (рис. 1а).
Если внешнее сопротивление R = 0,	контур превращается		в

идеальный (рис. 1б), в котором возникают незатухающие (рис. 2а)

электромагнитные колебания заряда	q на пластинах конденсатора,
напряжения на конденсаторе Uc.	и силы тока через катушку
индуктивности IL . Колебания в контуре сопровождаются взаимными
преобразованиями энергии электрического поля конденсатора		q	2	в
		2C
122

энергию магнитного поля катушки		LI 2
		.
		2
L	C	L	C

R

а)	б)
	Рисунок 1

1. Свободные гармонические колебания в идеальном

колебательном контуре.

В случае отсутствия внешнего напряжения в идеальном контуре по второму правилу Кирхгофа падение напряжения на пластинах

конденсатора ( U c

=

q

) равняется ЭДС самоиндукции ( ε i

= −L

dI

):

C

dt

q

= −L

dI

или

L

dI

+

q

= 0

(1)

dt

dt

C

C

Если (1) поделить на L

и учесть, что

I =

dq

, то:

dt

d 2 q

+

1

q = 0

(2)

dt 2

LC

Если в (2)

коэффициент

1

выразить как

ω02 , получим

LC

дифференциальное уравнение гармонического колебания заряда q в

идеальном контуре:

123

d 2 q	2			2
	+ ω0 q = 0	или	q + ω0		× q = 0	(3)
			&&

dt 2

Решение этого дифференциального уравнения дает уравнение гармонического колебания заряда на пластинах конденсатора в виде:

					q = q0 cos(ω0t + ϕ0 )	(4)
где q0 = qmax			– амплитуда колебаний;
ω0 =		1			– собственная циклическая частота колебаний;

LC

φ0 – начальная фаза колебаний; φ = (ω0t + φ0) – фаза колебаний.

Уравнение колебаний напряжения на пластинах конденсатора:

U c

=

q

=

q0

cos(ω0t + ϕ0 ) = U

0 cos(ω0t + ϕ0 )

(5)

C C

где

U 0 =

q

- амплитуда напряжения.

C

Уравнение колебаний тока в контуре:

I =

dq

= -ω0 q0 sin(ω0t + ϕ

0 ) = I 0 sin(ω0t + ϕ0 )

(6)

dt

где

I0 = ω0q0

- амплитуда тока.

Сравнение

выражений (4) и (6) показывает, что колебание тока

I опережают по

фазе колебания заряда

q

на π , т.е. когда

ток

2

получает максимальное значение, заряд (а также и напряжение) равняется нулю.

Таким образом, в идеальном контуре возникают гармонические

124

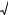
электромагнитные колебания с частотой ν = ω0	. Частота этих
2π

колебаний связана с периодом идеального колебательного контура

формулой Томсона:

	T =	1	=	2π	= 2π		(7)
						LC
	ν			ω0

2. Затухающие колебания в контуре

Любой реальный контур имеет сопротивление (т.е. R ≠ 0). По этой причине часть энергии контура тратится на нагрев деталей контура. Понятно, что свободные (при отсутствии внешнего напряжения) колебания должны со временем затухать.

Запишем закон Ома для реального контура, а потом учтем связь I, Uc , εi: с характеристиками контура:

IR + U c = ε i

dq

R +

q

= −L

dI

dt

dt

C

L

dI

+

dq

R +

q

= 0

dt

dt

C

Учтем, что I =

dq

→

dI

=

d 2 q

, и поделим все члены

dt

dt

dt 2

последнего уравнения на L.

Тогда получим:

d 2 q

+

R

dq

+

1

q = 0

dt 2

L dt

LC

Запишем это выражение в виде, который отвечает общему

дифференциальному уравнению затухающих колебаний заряда q:

125

d 2 q

dq

2

2

+ 2β

+ ω0 q = 0

или q

+ 2β × q + ω0

× q = 0

(8)

dt 2

dt

&&

&

где

β =

R

-

коэффициент затухания;

2L

ω

0 =

1

- собственная циклическая частота контура.

LC

Решением

дифференциального

уравнения

(8)

является

уравнение затухающих колебаний заряда на пластинах конденсатора в общем виде:

q = q0e-β ×t cos(ωt +ϕ0 )

(9)

где q0 e -β ×t - амплитуда колебания;

ω = ω02 - β 2 - циклическая частота затухающих колебаний.

Колебание напряжения на конденсаторе аналогичны

колебаниям заряда:
U c	=	q	=	q0	× e-β ×t cos(ωt + ϕ0 )	(10)
		C C

3. Исследование зависимости амплитуды затухающих колебаний

от времени.

В общем случае уравнение затухающих колебаний любого сигнала (х) можно записать в виде:

x = A	×e	-β ×t cos(ωt +ϕ	0	) = A(t )×cos(ωt +ϕ	0	)	(11)
0

Амплитуда затухающих колебаний уменьшается со временем по экспоненциальной зависимости:

126

A(t) = A0 ×e-β ×t

(12)

где A0 - начальная амплитуда (характеризует максимальное отклонение параметра х в момент времени t=0).

β– коэффициент затухания (характеризует скорость затухания колебаний).

График затухающих колебаний показан на рис. 2б, где пунктирная линия – это зависимость амплитуды от времени. Чем больше коэффициент затухания β (рис 2в), тем больше скорость затухания колебаний. (В качестве параметра х в случае электромагнитных колебаний может быть заряд q или напряжение

Uс на пластинах конденсатора колебательного контура).

х
хo
		а)
0	t
хo
	A e− β1t
	o
0	t	б)
	T

хo

Ao e− β2t

в)

0 t

127

Рисунок 2

Скорость затухания амплитуды колебаний характеризует

логарифмический декремент затухания λ, который определяется как натуральный логарифм отношения амплитуды колебаний A(t) в момент времени t к амплитуде A(t+T) в момент времени (t+T), то есть через время, равное периоду колебаний.

λ = ln	A(t)
		(13)
	A(t + T )

Логарифмический декремент затухания λ связан с коэффициентом затухания β и зависит от параметров колебательного

контура:
λ = β ×T = R ×T	(14)

2L

Вообще

основными

характеристиками

затухающих

электромагнитных колебаний являются:

A(t) = A0 ×e-β ×t -

амплитуда колебаний (в момент времени t=0 она

имеет максимальное значение А0)

ω =

ω02 - β 2

-

циклическая частота затухающих колебаний.

ω0 =

1

-

собственная циклическая частота контура.

LC

T =

2π

- период колебаний.

ω

β =

R

- коэффициент затухания.

2L

128

	λ = β ×T =					R	×T - логарифмический декремент затухания.
						2L
	τ =	1	=	T		= N e - время релаксации (характеризует время, за которое
		β		λ

амплитуда уменьшается в е раз).

Νе - число полных колебаний за время релаксации.

Q = π × N e	=	π	- добротность контура (характеризует число
		λ

колебаний за время релаксации).

Принципиальная схема исследования затухающих колебаний в контуре CLR показана на рис. 3.

РО

	C	L
			X
ПИ		Y

R

Рисунок 3

Импульс напряжения поступает от преобразователя импульсов (ПИ) на конденсатор С колебательного контура. Зарядка конденсатора осуществляется практически мгновенно, поскольку сопротивление цепи заряда мало. Затем конденсатор разряжается через сопротивление R и катушку индуктивности L. В колебательном контуре возникают затухающие колебания. Напряжение от конденсатора колебательного контура поступает на вход Y электронного осциллографа РО. При

129

включенной развертке на экране осциллографа можно наблюдать кривую затухающих колебаний напряжения на пластинах конденсатора Uc.

Порядок выполнения работы

1.Собрать (или проверить) схему установки. Включить установку в сеть, выждать 5 минут, пока прогреется осциллограф.

2.На магазине сопротивлений установить R1 = 0 Ом.

3.Измерить в миллиметрах амплитуды первых 8-ми периодов колебаний. Результаты измерений занести в табл.. 1.

4.Повторить пункты 2 - 3 для двух других значений сопротивления (R2> R1, R3 > R2). Результаты измерений занести в табл.. 1

5.Для каждого из отдельных значений Rі (отдельная строка в табл. 1) вычислить соотношения последовательных амплитуд, найти натуральные логарифмы этих соотношений (т.е. логарифмические декременты затухания λі). Результаты вычислений занести в табл. 2.

6.Для каждого из отдельных значений Rі вычислить и записать в табл. 2 среднее арифметическое значение λср

7.Построить график зависимости λср = f (R).

8.Сделать вывод о зависимости логарифмического декремента затухания от сопротивления, а также сделать сравнение полученной зависимости λср = f (R) с теоретической (14).

130