
- •Лекция 14. Неопределенный интеграл и его свойства План
- •1. Понятие первообразной функции. Свойства первообразной
- •2. Понятие неопределенного интеграла, свойства неопределенного интеграла
- •3. Метод замены переменной для вычисления неопределенного интеграла
- •4. Метод интегрирования по частям
- •5. Интегрирование рациональных функций. Метод неопределенных коэффициентов
- •Вопросы
3. Метод замены переменной для вычисления неопределенного интеграла
Теорема 2.
Пусть функция ![]() определена на интервале
определена на интервале ![]() и имеет тут первообразную
и имеет тут первообразную ![]() ,
и пусть функция
,
и пусть функция ![]() имеет производную везде на области
определения и принимает значения в
имеет производную везде на области
определения и принимает значения в ![]() .
Тогда функция
.
Тогда функция
![]() имеет первообразную
имеет первообразную
![]() .
Иначе говоря: Пусть надо вычислить
интеграл
.
Иначе говоря: Пусть надо вычислить
интеграл
![]() .
.
Во многих случаях удается в
качестве новой переменной выбрать такую
функцию ![]() ,
чтобы подинтегральное выражение можно
было представить в виде:
,
чтобы подинтегральное выражение можно
было представить в виде:
![]() ,
,
где ![]() — более удобная для интегрирования
функция, чем
— более удобная для интегрирования
функция, чем ![]() .
Тогда достаточно найти интеграл
.
Тогда достаточно найти интеграл
![]() ,
,
чтобы из него подстановкой
![]() получить искомый интеграл:
получить искомый интеграл:
![]() .
.
Доказательство.
Проверим, что полученная функция
![]() действительно будет первообразной для
действительно будет первообразной для
![]() :
:
![]() ,
,
что и требовалось доказать.
Проще всего замена проводится тогда, когда в представленном виде подинтегрального выражения в качестве множителя уже присутствует производная от новой переменной (хотя так бывает далеко не всегда).
Пример.
![]() .
.
Подинтегральное выражение
вместе с ![]() содержит в качестве множителя
содержит в качестве множителя ![]() .
Это говорит в пользу замены:
.
Это говорит в пользу замены: ![]() .
.
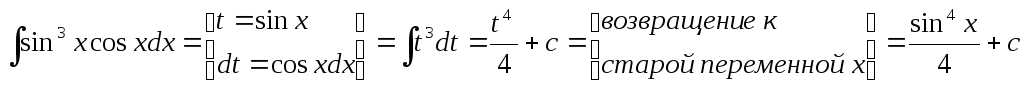 .
.
4. Метод интегрирования по частям
Теорема 3.
Пусть функции ![]() определены и дифференцированы на
определены и дифференцированы на ![]() ,
,
![]() —
непрерывны на
—
непрерывны на ![]() ,
и функция
,
и функция ![]() имеет первообразную на этом интервале.
Тогда функция
имеет первообразную на этом интервале.
Тогда функция ![]() также имеет первообразную на
также имеет первообразную на ![]() и выполняется равенство:
и выполняется равенство:
![]() ,
(3.9)
,
(3.9)
или, учитывая, что ![]() ,
а
,
а ![]() ,
формулу (3.9) можно записать в эквивалентном
виде:
,
формулу (3.9) можно записать в эквивалентном
виде:
![]() .
(3.10)
.
(3.10)
Формулы (3.9), (3.10) называются формулами интегрирования по частям.
Доказательство. По правилу вычисления производной произведения:
![]() .
(3*)
.
(3*)
Учитывая свойство 1 неопределенного интеграла, при интегрировании левой части (3*) получим:
![]() .
.
После интегрирования правой части (3*) имеем:
![]() .
.
Таким образом:
![]()
![]()
![]() .
.
Метод интегрирования
по частям часто используется в случаях,
когда подинтегральное выражение в
качестве множителей одновременно
содержит: степенную (![]() )
и тригонометрическую (
)
и тригонометрическую (![]() и т.д.) функции; степенную и обратную
тригонометрическую (
и т.д.) функции; степенную и обратную
тригонометрическую (![]() и т.д.); показательную (
и т.д.); показательную (![]() )
и тригонометрическую; логарифмическую
и тригонометрическую ( или обратную
тригонометрическую) и т.д.
)
и тригонометрическую; логарифмическую
и тригонометрическую ( или обратную
тригонометрическую) и т.д.
Пример.
Вычислить ![]() .
.
Подинтегральное выражение
содержит три множителя: ![]() .
Как разбить это выражение на части
.
Как разбить это выражение на части ![]() и
и ![]() ,
которые фигурируют в правой части
(3.10)? Ясно, что множитель
,
которые фигурируют в правой части
(3.10)? Ясно, что множитель ![]() может оказаться лишь в
может оказаться лишь в ![]() ,
а для двух других множителей возможны
варианты:
,
а для двух других множителей возможны
варианты: ![]() ,
тогда
,
тогда ![]() ,
или
,
или ![]() ,
тогда
,
тогда ![]() .
Рассмотрим оба варианта.
.
Рассмотрим оба варианта.
 .
(3.11)
.
(3.11)
Надо отметить, что при
восстановлении функции ![]() с помощью операции
с помощью операции ![]() ,
достаточно взять лишь одну первообразную.
В нашем примере мы выбираем
,
достаточно взять лишь одну первообразную.
В нашем примере мы выбираем ![]() в конкретном виде:
в конкретном виде: ![]() ,
а не в общем виде:
,
а не в общем виде: ![]() .
Произвольная постоянная при вычислении
неопределенного интеграла учитывается
в окончательном его выражении.
.
Произвольная постоянная при вычислении
неопределенного интеграла учитывается
в окончательном его выражении.
Сделанная разбивка подинтегрального выражения на части привела к значительному его упрощению - табличному интегралу в правой части (3.11). Таким образом:
![]() .
(3.12)
.
(3.12)
Посмотрим, как повлияет на сложность вычислений другой вариант разбивки, упомянутый выше:
 (3.13)
(3.13)
Формула интегрирования по частям используется вообще с целью упрощения подинтегрального выражения, но, как видно из правой части (3.13), в данном случае мы не упростили, а усложнили интеграл. Понятно, что из двух возможных вариантов разбивки надо выбирать первый.
