Производные высших порядков

Производная от функции является также функцией от и может быть дифференцируема.

Производная от производной функции называется про­изводной второго порядка или второй производной функции и обо­значается: . Таким образом,

.

Вторая производная имеет простой механический смысл. Пусть — закон движения материальной точки, тогда первая про­изводная определяет скорость движения . Вторая же про­изводная есть скорость изменения скорости движения, т. е. ускоре­ние .

Аналогично вводятся производные третьего, четвертого и более высоких порядков.

Производной -го порядка от функции называется про­изводная от производной (– 1)-го порядка.

Рассмотрим примеры нахождения производных высших по­рядков.

Пример. Найти производную -го порядка от функции .

Решение. Выполняя последовательное дифференцирование, находим:

. . . . . . . . . . . . . . . . . . . .

.

Дифференцирование неявно заданных функций

Пусть функция задана уравнением . В этом случае говорят, что функция задана неявно. Предположим, что функция дифференцируема. Если в уравнении под подразумевать функцию , то это уравнение обращается в тождество по аргументу : . Дифференцируем его по , считая, что есть функция . Получаем новое уравнение, содержащее , и . Разрешая его относительно , находим производную искомой функции , заданной в неявном виде.

Пример. Найти производную функции , заданной неявно.

Решение. Дифференцируя по неявную функцию и считая, что — функция от , имеем ,

,

.

Отметим, что в этом случае .

По определению вторая производная от функции есть производная от первой производной. Следовательно, для нахождения второй производной надо продифференцировать найденную первую производную по аргументу , продолжая рассматривать как функцию от . В выражение для второй производной в общем случае войдут , и . Подставляя вместо его значение, находим , зависящую только от и . Аналогично поступаем при нахождении производных более высоких порядков.

Пример. Найти производную второго порядка от функции , за­данной уравнением .

Решение. Найдем первую производную

.

Диф­ференцируя данное уравнение вторично, получаем .

Так как , имеем .

Дифференцирование функций, заданных параметрически

Пусть функция задана параметрически:

.

Найдем первую производную функции по переменной , то есть

.

Т.е. .

Найдем вторую производную от функции по переменной . Прямое дифференцирование функции возможно только по параметру и даст в результате смешанную производную . Поэтому для нахождения второй производной от функции по переменной предварительно представим ее в виде:

Тогда .

Аналогично находится третья производная:

и производные высших порядков.

Пример. Найти производные первого и второго порядков от функции , за­данной параметрически:

.

Решение. Найдем первую производную функции по переменной , то есть

.

, .

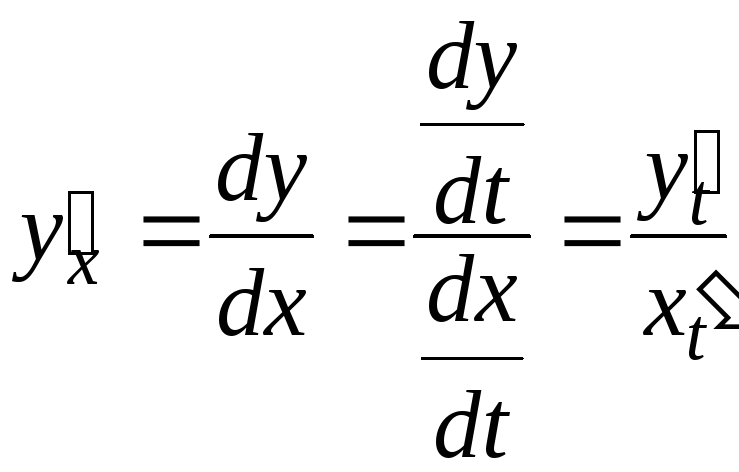Следовательно .

Найдем вторую производную от функции по переменной .

.

.

Следовательно .

Ответ: .

Дифференциалы высших порядков

Рассмотрим функцию . Дифференциал этой функции = зависит от и , причем от не зависит, так как приращение в данной точке можно выбирать независимо от точки . В этом случае в формуле первого дифференциала будет постоянным. Следовательно, если выражение зависит только от , то его мож­но дифференцировать по .

Определение. Дифференциал от дифференциала функции в данной точке называется дифференциалом второго порядка или вторым дифференциалом.

Дифференциал второго порядка обозначается или . Таким образом,

.

Аналогично дифференциал третьего порядка от функции

.

Вообще дифференциал -го порядка (или -й дифференциал) функции определяется как дифференциал от дифференциала (–1)-го порядка:

.

Найдем выражение для второго дифференциала функции , полагая в формуле первого дифференциала постоянным. Тогда

,

т. е. дифференциал второго порядка вычисляется по формуле:

.

Откуда можно выразить производную функции второго порядка как отношение ее дифференциала второго порядка к второй степени дифференциала независимой переменной:

.

Аналогично .

Можно установить справедливость формулы для дифференциала -го порядка

.

Отсюда следует, что производная -го порядка есть отношение ее дифференциала -го порядка к -й степени дифференциала не­зависимой переменной:

.

При этом предполагаем, что аргумент функции является независимой переменной.

Выведем теперь формулы для вычисления дифференциалов высших порядков для сложной функции , когда аргумент является дифференци­руемой функцией независимой переменной. Но для одного и того же , но для разных (и, следовательно, для разных ) приращения различны, т. е. в этом случае нельзя счи­тать независимыми от , так как является дифференциалом функции:

.

Поэтому при вычислении по определению

мы должны считать его дифференциалом от произведения двух функций и , т. е.

Итак,

Таким образом, в случае, когда аргумент не является неза­висимой переменной, второй дифференциал определяется форму­лой, состоящей из двух слагаемых.

Приведем формулу для вычисления дифференциала третьего порядка:

Из полученных формул для , следует, что при вычислении дифференциалов более высоких порядков от сложной функции про­исходит нарушение инвариантности формы. Другими словами, фор­мулы для дифференциалов порядка выше первого различны. Их вид зависит от того, является ли аргумент независимой переменной или дифференцируемой функцией другой переменной (Напомним, что для дифференциала первого порядка его форма записи остается неизменной).