Глава 4. Комплексные числа.

Содержание темы.

Теорема о существовании поля комплексных чисел. Действия над комплексными числами в алгебраической форме. Геометрическая интерпретация комплексных чисел, тригонометрическая форма записи, действия над комплексными числами в тригонометрической форме.

Основные умения и навыки, которыми должны овладеть студенты в процессе изучения этой темы:

- уметь изображать комплексные числа на координатной плоскости в виде точек и радиус-векторов и наоборот;

- уметь находить модуль и аргумент zC, переходить от алгебраической формы записи комплексного числа к тригонометрической и наоборот;

- уметь выполнять арифметические операции над комплексными числами в алгебраической и тригонометрической форме, понимать их геометрический смысл;

- использовать полученные знания при решении задач алгебры и геометрии.

Все теоретические положения и практические выводы этой темы вытекают из теоремы о существовании поля комплексных чисел.

Теорема 1: Существует единственное, с точностью до изоморфизма, поле С, в котором выполняются следующие условия:

1. Поле R является подполем поля С.

2. i² = -1

3. zC х, yR: z = x + iy

Запись комплексного числа z в виде х + iy называется его алгебраической формой, при этом (х) называют действительной частью комплексного числа, iy - мнимой частью, а (у) – коэффи-циентом мнимой части. Обозначение: Re z - действительная часть, Im z - мнимая часть комплексного числа.

Так как (z = х + iy)  (C = R x R), то с геометрической точки зрения, любое комплексное число имеет две равноправные геометрические интерпретации (модели).

а) точка координатной плоскости А (х, у);

б) радиус-вектор с концом в точке с координатами (х, у)

Геометрический подход к понятию комплексного числа позволяет записывать его в так называемой тригонометрической форме.

Для этого вводятся понятия модуля и аргумента комплексного числа.

Определение 1: Модулем комплексного числа z называется арифметическое значение корня квадратного из х² + у², то есть

Это понятие является обобщением понятия «абсолютная величина действительного числа», так как, если z = х + 0i, то .

С геометрической точки зрения, модуль комплексного числа - это длина радиус-вектора ОА или расстояние от начала координат до точки с координатами (х, у).

Определение 2: Аргументом комплексного числа z называют угол  между положительным направлением оси и радиус - вектором, отсчитываемым против часовой стрелки.

Из этого определения следует, что аргумент комплексного числа определяется неоднозначно, а с точностью до числа, кратного 2. Поэтому на практике, в качестве аргумента, обычно берут наименьший положительный или наименьший по абсолютной величине угол, который обозначают  =arg z и находят из соотношений:

cos  = , sin  = , 0    2

тогда х + iy = и мы получим тригонометрическую формулу записи комплексного числа.

Во избежание ошибок при нахождении аргумента комплексного числа z его нужно предварительно изобразить на координатной плоскости.

Модуль и аргумент комплексного числа z являются известными из курса геометрии полярными координатами точки, соответ-ствующей числу z. При этом полярной осью служит ось

Понятие модуля и аргумента комплексного числа z позволяют записать это число в тригонометрической форме.

Пример 1. Комплексное число z = записать в тригонометрической форме.

1. Изобразим данное комплексное число на координатной плоскости. Это будет радиус-вектор с концом в точке (, -1) (см. рисунок)

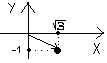
2. Найдем его модуль | z | = || =

3. Найдем аргумент из соотношений

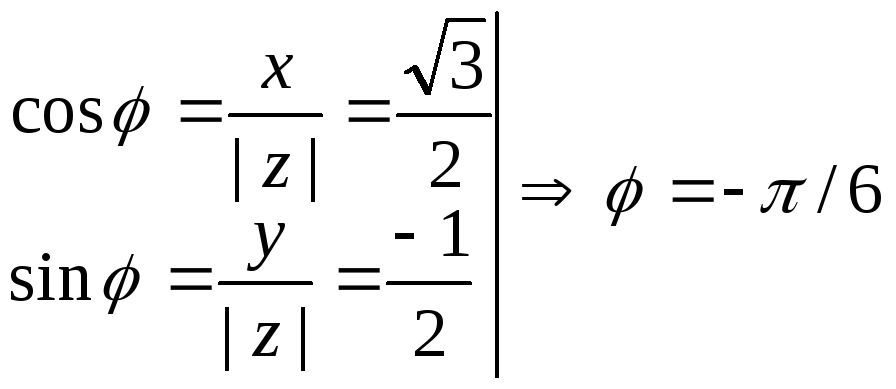или j = 11p/6

Таким образом,

Существование двух форм записи одного и того же комплексного числа z = х + iy = |z| (cosj + sinj) позволяет выполнять алгебраические операции на множестве С в той форме, которая наиболее удобна в каждом конкретном случае.

Теорема 2. Если z₁ =x₁ + iy₁, z₂ =x₂ + iy₂, то

1. z₁+z₂ = (x₁+x₂) + i(y₁+y₂)

2. z₁-z₂ = (x₁-x₂) + i(y₁-y₂)

3. z₁z₂ = (x₁x₂ -y₁y₂) + i(x₁y₂ + x₂ y₁)

4.

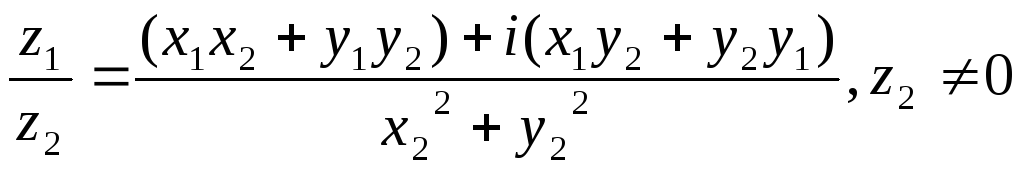
5. На практике обычно формулы 3), 4) не запоминают, а руководствуются такими мнемоническими правилами:

а) чтобы перемножить два комплексных числа, нужно перемножить их как два двучлена;

б) чтобы разделить z₁ на z₂  0, нужно числитель и знаменатель домножить на комплексное число, сопряженное знаменателю и выполнить указанные действия (z = х – iy называют сопряженным по отношению к z = х + iy).

Извлечение в алгебраической форме практически не используется.

Пример 2. z₁ = -2 + 5i, z₂ = 1 + 3i

z₁ + z₂= -1 + 8i

z₁ - z₂= -3 + 2i

z₁• z₂ = (-2 + 5i)(1 + 3i) = (-2 - 6i + 5i + 15i²) = -17 – i

Теорема 3. Если z₁=|z₁|(cosj+i sinj), z₂=|z₂|(cos+i sin), то

1) z₁•z₂= |z₁| |z₂| [cos(j+) + i sin (j+)]

2) z₁ⁿ = |z₁|ⁿ [cos(nj) + i sin (nj)]

3)

4)k = 0,1, 2,.., (n-l)

Операции сложения и вычитания в тригонометрической форме на практике не выполняются.

Пример 3.

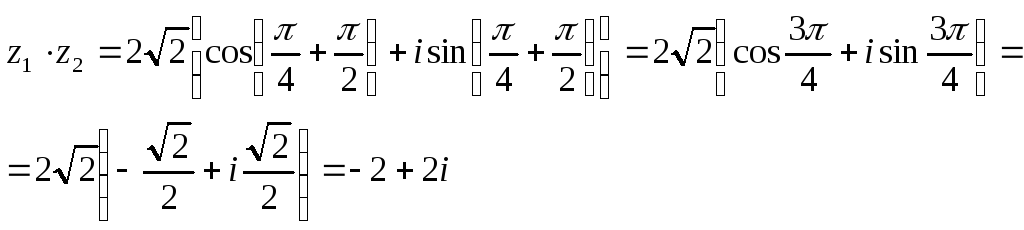
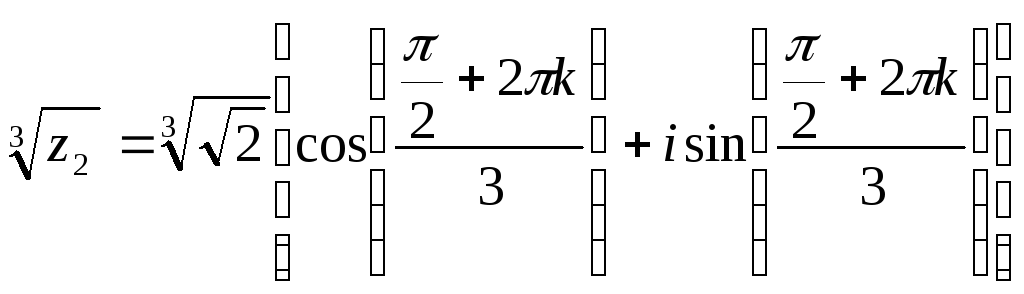k = 0, 1, 2

Операции над комплексными числами также могут быть осмыслены с геометрической точки зрения. Так, операциям сложения и вычитания двух комплексных чисел соответствуют операции сложения и вычитания двух векторов по правилу параллелограмма.

рис.1

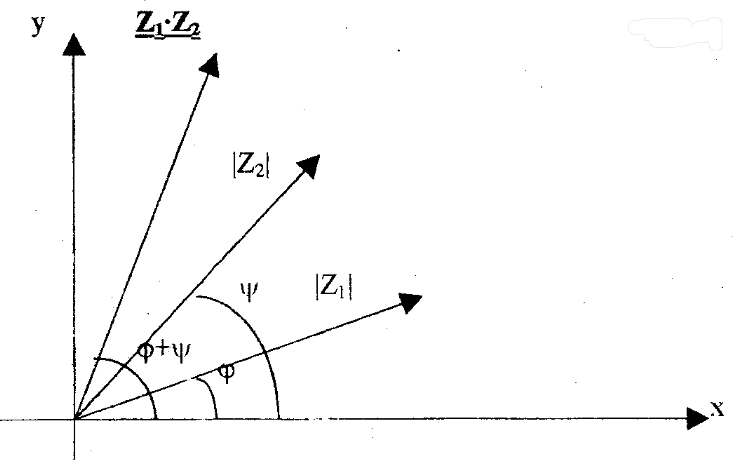
рис. 2

Пример 4. Пусть z₁ = 3 + i, z₂ = 1 – 3i. Найти z₁ + z₂ и z₁ - z₂ геометрически.

Изображаем каждое комплексное число в виде радиус-вектора, затем строим параллелограмм и находим вектор, соответствующий z₁ + z₂ и z₁ - z₂ (см. рис.1)

Геометрический смысл произведения двух комплексных чисел можно выяснить, если перемножить эти числа в тригонометрической форме. Пусть Z₁ = |Z₁|(cos + i sin), Z₁  0,

Z₂ = |Z₂| (cos + i sin), Z₂  0, тогда

z₁  z₂ = |z₁||z₂| [cos( + ) + i sin(+ )]

При умножении двух комплексных чисел в тригонометрической форме их модули перемножаются, аргументы складываются. Следовательно, чтобы умножить комплексное число z₁ на z₂ нужно длину вектора z₁ изменить в |z₂| раза (растянуть или сжать), а затем полученный вектор повернуть вокруг начала координат на угол arg z₂ (см. рис. 2).

Геометрический смысл операции состоит в делении окружности радиуса наn равных частей.

Пример 5. Вычислить и изобразить все его значения геометрически.

Представим комплексное число z = - 4 в тригонометрической форме. Для этого найдем его модуль и аргумент. |-4|=4arg(-4)=, -4 = 4 (cos + i sin)

Тогда k = 0,1,2,3

Придавая параметру (k) значения 0, 1,2, 3, получим четыре значения корня четвертой степени из -4.

Изобразим найденные корни на комплексной плоскости, они делят

окружность радиуса 2 на четыре равные части. Кроме этого, мы вписали в эту окружность правильный четырех-угольник (квадрат).

Часто при решении задач используется геометрический смысл модуля разности двух комплексных чисел, как расстояния между двумя точками на плоскости. |z₁ - z₂| = (z₁, z₂)

Задача 1. Найти геометрическое место точек, для которых |z - (2 + i)| < 3

Геометрический смысл этого неравенства состоит в том, что расстояние от точки (2, 1) до точек (х, у) не должно быть больше трех единиц.

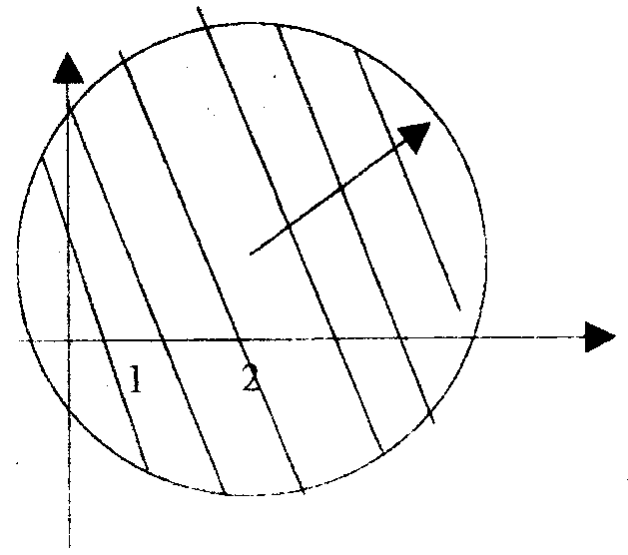
Это значит, что искомым геометрическим местом точек является открытый круг (точки окружности ему не принадлежат) с центром в точке (2, 1) и радиусом r = 3

Этот ответ на вопрос задачи можно было получить и алгебраически, используя определение модуля

|(x + iy) - (2 + i)| < 3  |(x- 2) + i(y -1)| < 3 

 (x-2)² + (y-l)²<9

Из курса геометрии известно, что равенство (х-2)²+(у-1)²=3² есть уравнение окружности с центром в точке (2, 1) и r = 3, тогда искомым г.м.т. будет внутренняя часть этого круга.