§3. Подгруппа. Достаточные условия подгруппы.

Определение 1. Пусть <G, *> - группа и HG. Подалгебра <Н, *> группы <G, *> называется подгруппой группы G, если алгебра <Н, *> сама является группой относительно операции *.

Если Н - подгруппа группы G, то пишут Н < G.

Замечание. Для того, чтобы выяснить, является ли некоторое множество HG подгруппой группы G относительно операции *, заданной на G, достаточно проверить следующие условия:

а)  а  Н,  b  Н, а * b  H - условие замкнутости,

б)  а  Н, а'  Н - условие симметризуемости,

называемые в дальнейшем достаточными условиями подгруппы.

Действительно, если  а  Н, а'  Н, то а * а'Н. Так как а * а' = е, то нейтральный элемент е группы G также принадлежит и множеству Н. Операция * на множестве Н является ассоциативной, так как она ассоциативна на множестве G, включающем Н. Итак, <Н, *> - группа.

Пример 1. Рассмотрим аддитивные группы чисел <Z, +>, <2Z, +>, <Q, +>, <R, +>. Имеет место следующая цепочка 2Z<Z<Q<R.

Покажем, например, что 2Z<Z. Действительно, 2ZZ. Кроме того:

а)  a, b  2Z, a + b  2Z,

б)  a  2Z, -a  2Z.

Таким образом, достаточные условия подгруппы выполнены.

Аксиома нейтрального элемента выполнима на 2Z, так как из условий а) и б) следует, что а + (- а) = 0, 02Z. Аксиома ассоциативности тоже выполнима, так как 2ZZ. Таким образом, 2Z < Z.

Пример 2. Подгруппами абстрактной группы G будут так называемые тривиальные подгруппы - сама группа G, т е G<G и группа Е={е, еG}, т.e. E<G.

Пример 3. Показать, что алгебра <R⁺, +> не является подгруппой аддитивной группы <R, +>.

Действительно, R⁺  R. Кроме того,

а)  a, b  R⁺. (a + b)R⁺. - условие замкнутости выполнено,

б) aR⁺ -aR⁺, - условие симметризуемости не выполняется на R⁺. Следовательно, алгебра < R⁺ , +> не является подгруппой группы R, +>.

§4. Кольцо, поле, линейное пространство.

Определение 1. Алгебра <А, +, •> - называется кольцом, если бинарные операции +, • удовлетворяют условиям:

1 -4) <А, +> - коммутативная группа

5) " a, b, c Î A, a • (b + c) = ab + ас

(b + с) • а = bа + са

Из определения следует, что любое кольцо - это коммутативная группа, в которой операция сложения связана с операцией умножения левым и правым дистрибутивными законами. На операцию умножения в общем случае никаких ограничений не накладывается. Если операция умножения дополнительно обладает свойствами коммутативности, ассоциативности и нейтральным элементом, то кольцо называют ассоциативно - коммутативным кольцом с единицей.

Пример 1. <Z, +, •>, <Q, +, •>, <R, +, •>, <Z_m, +, •> - коммутативные кольца.

Определение 2. Алгебра <А, +, • > называется полем, если бинарные операции сложения и умножения удовлетворяют условиям (аксиомам):

1 -4) < А, +> - коммутативная группа

5-8) <А\{0}, •> - коммутативная группа

9) " a, b, c Î A, a • (b + c) = ab + ас

(b +с) • а = bа + са

Из определения следует, что любое поле - это аддитивная и мульти­пликативная группа одновременно, а также коммутативно-ассоциативное кольцо с единицей, в котором каждый ненулевой элемент обратим.

Пример 2. <Q, +, •>, <R, +, • >, <Z°_P, +, • > - поля.

Пусть дано не пустое множество V и поле F.

Элементы множества V будем обозначать малыми буквами латинского алфавита и называть векторами. Элементы поля F будем обозначать малыми буквами греческого алфавита и называть скалярами.

Определим на множестве V бинарную операцию сложения векторов : VVV, +<a, b>  а + b

и внешнюю композицию w: F•VV

w: <, а>  а (умножение вектора на скаляр),

которую при фиксированном значении скаляра можно считать унарной операцией на множестве V.

Определение 3. Алгебра <V, +{w | F}> называется линейным векторным пространством относительно операции сложения векторов и умножения вектора на скаляр, если 1-4) <V, +> - коммутативная группа.

5)  a, b  V    F, (а+b) = а + b

6)  ,   F  a  V, (+) • a = a + a

7)  ,   F  a  V, ( • ) • a = a • (b • a)

8) " a Î V, la = a

Из определения следует, что любое линейное векторное пространство является аддитивной коммутативной группой.

Примеры 3. <Rⁿ, + {wl | R}> - арифметическое линейное векторное пространство.

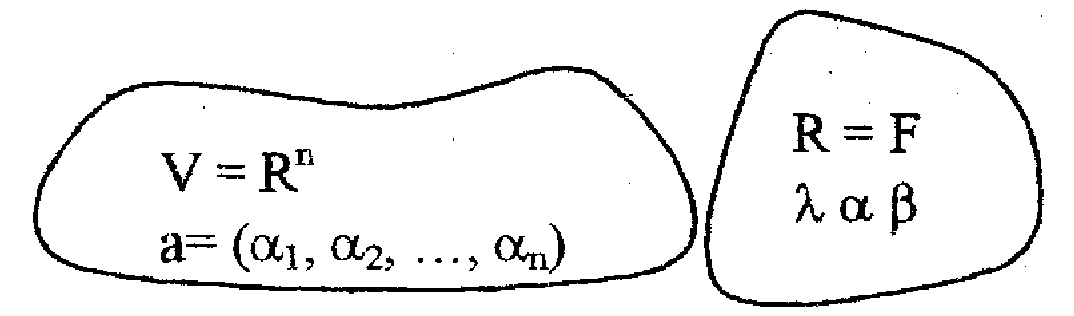
Роль векторов в этом пространстве играют арифметические векторы вида: a =(₁ ,₂, ...,_n)

Операция  - это операция сложения таких векторов, операция wl -это операция умножения арифметического вектора на действительное число. Легко проверить, что эти операции удовлетворяют условиям 1-8. Покажем, например, что <Rⁿ, +> - коммутативная группа.

1. Так как операция + по определению является бинарной операцией на Rⁿ, то < Rⁿ , +> - алгебра.

2.  a, b  Rⁿ, a + b = b + a

Действительно, пусть a =(₁ ,₂, ...,_n), b = (₁ ₂, ... ,_n)

Тогда а+b=(a₁+₁,a₂ +₂, ...,a_n +_n), b+a=(₁+a₁ ,₂+a₂, ...,_n+a_n)

Так как операция сложения действительных чисел коммутативна, то a+b=b+a

3. " a, b, cÎ Rⁿ, (a+b)+c=a+(b+c) проверяется аналогично.

4. Роль нуля будет играть вектор  =(0,0 .. 0).

5. " a ÎV  -а : а + (- а) = (-а) + а =  действительно, если a =(a₁ ,a₂, ...,a_n), то -a =(-a₁ ,-a₂, ...,-a_n), которые в сумме дадут нулевой вектор.

Итак, <Rⁿ, +> - коммутативная группа. Остальные условия в определении линейного пространства проверить самостоятельно.

Замечание. Линейные пространства <R¹, + {w | R}>, <R², +{w | R}>, <R³, +{w | R}> имеют наглядную геометрическую интерпретацию:

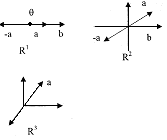
R¹ - множество радиусов-векторов на прямой;

R² - множество радиусов-векторов на плоскости;

R³ - множество радиусов-векторов в пространстве.